2010年山东省菏泽市中考数学试题

2010年山东省菏泽市中考数学试题

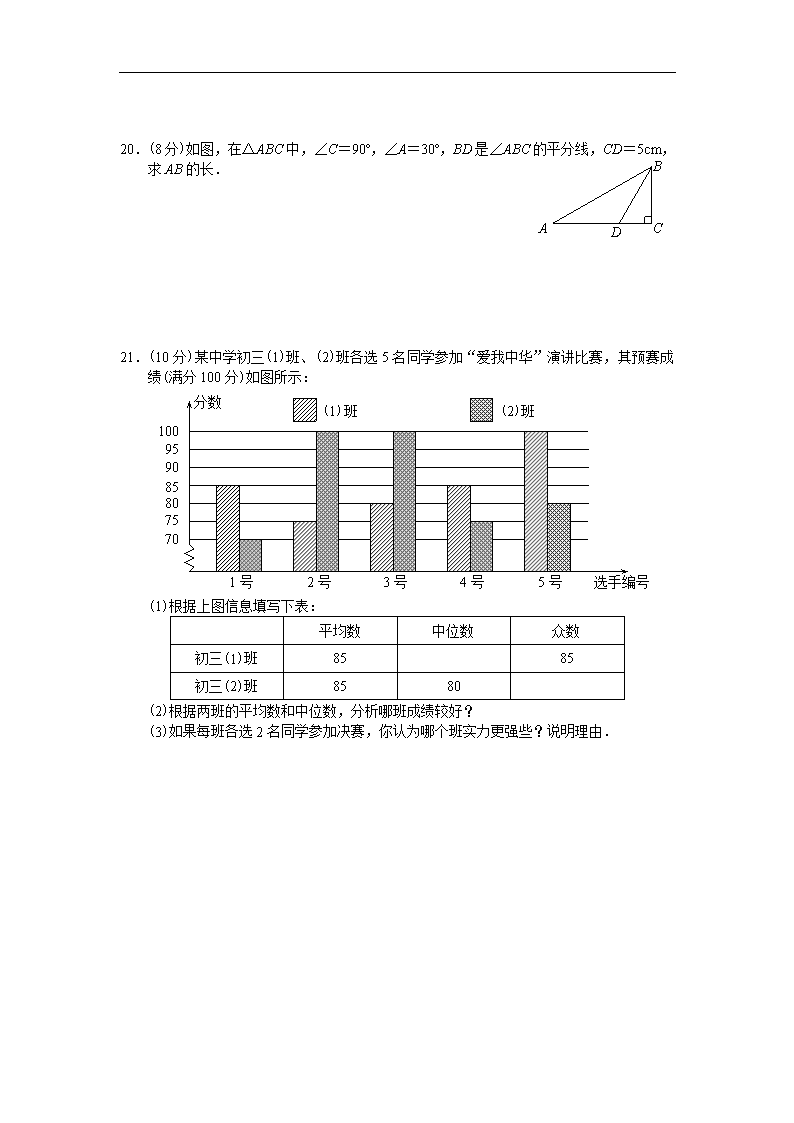
菏泽市2010年初中学业水平考试 数学试题 一、选择题（本大题共10小题，每小题3分，满分30分）‎ ‎1．2010年元月19日，山东省气象局预报我市元月20日的最高气温是‎4℃‎，最低气温是－‎6℃‎，那么我市元月20日的最大温差是（ ）‎ A．‎10℃‎ B．‎6℃‎ C．‎4℃‎ D．‎‎2℃‎ ‎2．负实数a的倒数是（ ）‎ A．－a B． C．－ D．a ‎3．下列运算正确的是（ ）‎ A．(a＋b)(b－a)＝a2－b2 B．(a－2)2＝a2－4‎ C．a3＋a3＝‎2a6 D．(－‎3a2)2＝‎9a4‎ ‎4．如图是一个由多个相同小正方体堆积而成的几何体的俯视图，图中所示数字为该位置小正方体的个数，则这个几何体的左视图是（ ）‎ A B M N C E F P Q ‎1‎ ‎3‎ ‎1‎ ‎2‎ ‎1‎ A． B． C． D．‎ ‎5．如图，直线PQ∥MN，C是MN上一点，CE交PQ于 A，CF交PQ于B，且∠ECF＝90º．若∠FBQ＝50º，‎ 则∠ECM＝（ ）‎ A B C D G A1‎ A．60º B．50º C．40º D．30º ‎6．如图，在矩形纸片ABCD中，AB＝4，AD＝3．折叠纸片使 AD边与对角线BD重合，折痕为DG，点A落在点A1处，‎ 则△A1BG的面积与矩形ABCD的面积的比为（ ）‎ A B C D G E F A． B． C． D． ‎7．如图，在正方形铁皮中，剪下一个圆和一个扇形，使余料尽量少．‎ 用圆做圆锥的底面，用扇形做圆锥的侧面，正好围成一个圆锥．‎ 若圆的半径为r，扇形的半径为R，则（ ）‎ A．R＝2r B．R＝r C．R＝3r D．R＝4r A B D E C F ‎8．如图，在菱形ABCD中，∠B＝60º，AB＝‎2cm，E、F分别是BC、‎ CD的中点，连接AE、EF、AF，则△AEF的周长为（ ）‎ A．‎2cm B．‎3cm C．‎4cm D．‎‎3cm ‎9．某种气球内充满了一定质量的气体．当温度不变时，气球内 气体的气压P(kPa)是气体体积V(m3)的反比例函数，其图象 O ‎(1.6，60)‎ P/kPa V/m3‎ ‎60‎ ‎1.6‎ 如图所示．当气球内气体的气压大于120kPa时，气球将爆炸．‎ 为了安全，气体的体积应该（ ）‎ A．不大于m3 B．小于m3‎ C．不小于m3 D．小于m3‎ ‎10．‎ 某医院决定抽调甲、乙、丙、丁4名医护人员参加抗震救灾，先随机地从这4人中抽取2人作为第一批救灾医护人员，那么丁被抽到作为第一批救灾医护人员的概率是（ ）‎ A． B． C． D． 二、填空题（本大题共8小题，每小题3分，满分24分）‎ ‎11．分解因式：a3－‎6a2b＋9ab2＝ ．‎ ‎12．月球距离地球地面为‎384000000m，将这个距离用科学记数法表示(保留两个有效数字)应为 m．‎ ‎13．若关于x的不等式‎3m－2x＜5的解集是x＞2，则实数m的值为 ．‎ ‎14．已知2是关于x的方程x2＋4x－p＝0的一个根，则该方程的另一个根是 ．‎ ‎15．已知点P的坐标为(m，n)，O为坐标原点．连接OP，将线段OP饶O点顺时针旋转90º得OP1，则点P1的坐标为 ．‎ A B C D O ‎16．刘谦的魔术表演风靡全国．小明也学起刘谦，发明了一个魔术盒，当任意实数对(a，b)进入其中时，会得到一个新的实数：a2＋b－1，例如把(3，－2)放入其中，就会得到32＋(－2)－1＝6．现将实数对(－2，－3)放入其中，得到的实数是 ．‎ ‎17．如图，在正方形ABCD中，O是CD上的一点，以O为圆心、‎ OD为半径的半圆恰好与以B为圆心、BC为半径的扇形的弧外 切，则∠OBC的正弦值为 ．‎ ‎18．如图，三角板ABC的直角边AC、BC的长分别为‎40cm和‎30cm，‎ A B C D E F G C1‎ B1‎ A1‎ 点G在斜边AB上，且BG＝‎30cm．将这个三角板以G为中心按 逆时针旋转90º至△A1B‎1C1的位置，那么旋转前后两个三角板重 叠部分(四边形DEFG)的面积为 ．‎ 三、解答题（本大题共6小题，满分66分）‎ ‎19．（每小题4分，满分12分）‎ ‎(1)计算：．‎ ‎(2)解不等式组：‎ ‎(3)解分式方程：．‎ A B C D ‎20．(8分)如图，在△ABC中，∠C＝90º，∠A＝30º，BD是∠ABC的平分线，CD＝‎5cm，求AB的长．‎ ‎21．(10分)某中学初三(1)班、(2)班各选5名同学参加“爱我中华”演讲比赛，其预赛成绩(满分100分)如图所示：‎ 分数 ‎(1)班 ‎(2)班 ‎1号 ‎2号 ‎3号 ‎4号 ‎5号 选手编号 ‎70‎ ‎100‎ ‎95‎ ‎90‎ ‎85‎ ‎80‎ ‎75‎ ‎(1)根据上图信息填写下表：‎ 平均数 中位数 众数 初三(1)班 ‎85‎ ‎85‎ 初三(2)班 ‎85‎ ‎80‎ ‎(2)根据两班的平均数和中位数，分析哪班成绩较好？‎ ‎(3)如果每班各选2名同学参加决赛，你认为哪个班实力更强些？说明理由．‎ A E B O C D ‎22．(12分)如图，在△AOB中，OA＝OB，∠A＝30º，⊙O经过AB的中点E分别交OA、OB于C、D两点，连接CD．‎ ‎(1)求证：AB是⊙O的切线．‎ ‎(2)求证：AB∥CD．‎ ‎(3)若CD＝4，求扇形OCED的面积．‎ ‎23．(12分)我市为绿化城区，计划购买甲、乙两种树苗共计500棵，甲种树苗每棵50元，乙种树苗每棵80元，调查统计得：甲、乙两种树苗的成活率分别为90%、95%．‎ ‎(1)如果购买两种树苗共用28000元，那么甲、乙两种树苗各买了多少棵？‎ ‎(2)市绿化部门研究决定，购买树苗的钱数不得超过34000元，应如何选购树苗？‎ ‎(3)要使这批树苗的成活率不低于92%，且使购买树苗的费用最低，应如何选购树苗？最低费用是多少？‎ ‎24．(12分)如图，抛物线y＝ax2＋bx＋c经过原点O，与x轴交于另一点N，直线y＝kx＋4与两坐标轴分别交于A、D两点，与抛物线交于点B(1，m)、C(2，2)．‎ ‎(1)求直线与抛物线的解析式．‎ ‎(2)若抛物线在x轴上方的部分有一动点P(x，y)，设∠PON＝，求当△PON的面积最大时tan的值．‎ P(x，y)‎ A B C O N D y x y＝kx＋4‎ ‎(3)若动点P保持(2)中的运动线路，问是否存在点P，使得△POA的面积等于△PON的面积的？若存在，请求出点P的坐标；若不存在，请说明理由．‎