- 2021-04-17 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019七年级数学上册 2等式的基本性质
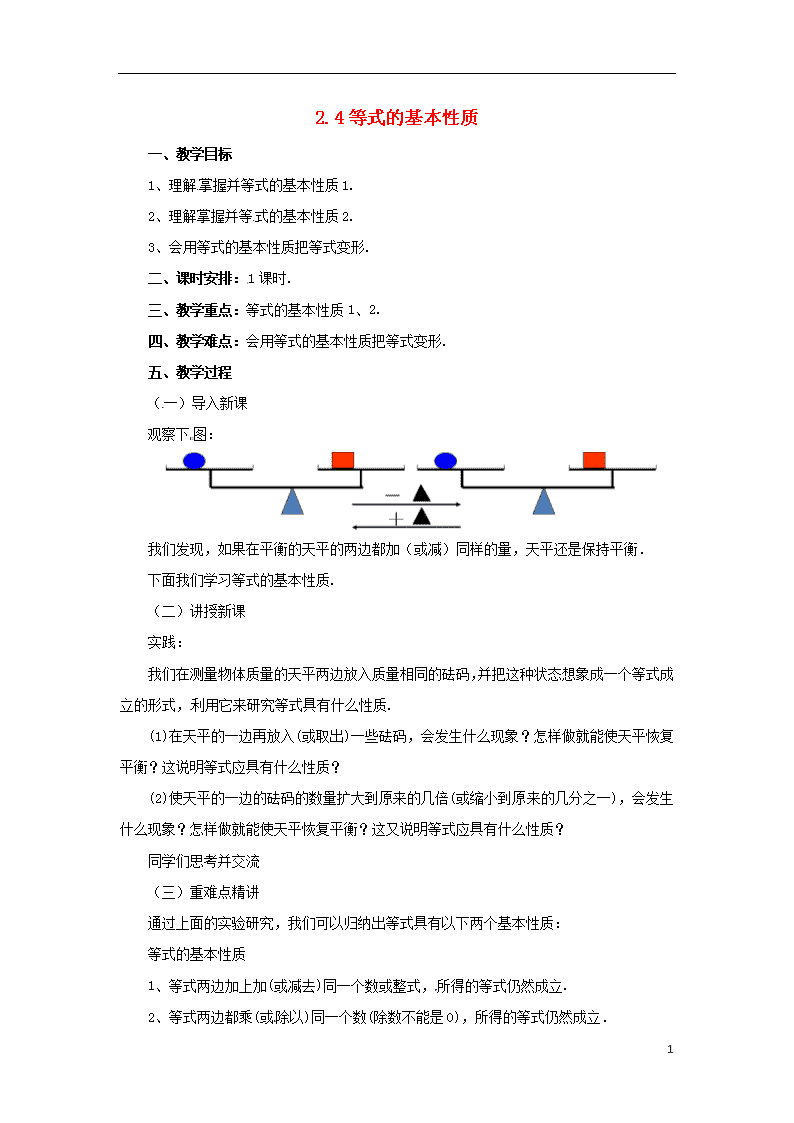
2.4等式的基本性质 一、教学目标 1、理解掌握并等式的基本性质1. 2、理解掌握并等式的基本性质2. 3、会用等式的基本性质把等式变形. 二、课时安排:1课时. 三、教学重点:等式的基本性质1、2. 四、教学难点:会用等式的基本性质把等式变形. 五、教学过程 (一)导入新课 观察下图: 我们发现,如果在平衡的天平的两边都加(或减)同样的量,天平还是保持平衡. 下面我们学习等式的基本性质. (二)讲授新课 实践: 我们在测量物体质量的天平两边放入质量相同的砝码,并把这种状态想象成一个等式成立的形式,利用它来研究等式具有什么性质. (1)在天平的一边再放入(或取出)一些砝码,会发生什么现象?怎样做就能使天平恢复平衡?这说明等式应具有什么性质? (2)使天平的一边的砝码的数量扩大到原来的几倍(或缩小到原来的几分之一),会发生什么现象?怎样做就能使天平恢复平衡?这又说明等式应具有什么性质? 同学们思考并交流 (三)重难点精讲 通过上面的实验研究,我们可以归纳出等式具有以下两个基本性质: 等式的基本性质 1、等式两边加上加(或减去)同一个数或整式,所得的等式仍然成立. 2、等式两边都乘(或除以)同一个数(除数不能是0),所得的等式仍然成立. 3 我们可以用数学式子表示等式的基本性质: 1、如果a=b,c表示任意的数或整式,那么a+c=b+c. 2、如果a=b,c表示任意的数,那么ac=bc; 如果a=b,c≠0,那么. 典例: 例、用适当的数或式子填空,使得到的结果仍是等式,并说明是根据等式的哪条基本性质及怎样变形(改变式子的形状)的. (1)如果3x=7-5x,那么3x+_______=7. (2)如果,那么x=_______. 解:(1)3x+5x=7. 根据等式的基本性质1,在等式的两边都加上5x. (2)x=. 根据等式的基本性质2,在等式的两边同时乘. 跟踪训练: 用适当的数或式子填空,使得到的结果仍是等式,并说明是根据等式的哪条基本性质及怎样变形(改变式子的形状)的. (1)如果2x=6-3x,那么3x+_______=7. (2)如果,那么y=_______. 解:(1)3x+3x=6. 根据等式的基本性质1,在等式的两边都加上5x. (2)y=-8. 根据等式的基本性质2,在等式的两边同时乘-4. (四)归纳小结 通过这节课的学习,你有哪些收获?有何感想?学会了哪些方法?先想一想,再分享给大家. (五)随堂检测 1、根据等式的性质,方程5x-1=4x变形正确的是( ) 3 A.5x+4x=-1 B. x-=2x C.5x-4x=-1 D.5x+4x=1 2、下列四组变形中,变形正确的是( ) A.由5x+7=0,得5x=-7 B.由2x-3=0,得2x-3+3=0 C.由=2,得x= D.由5x=7,得x=35 3、用适当的数或式子填空,使所得的结果仍是等式,并说明根据哪一条性质以及怎样变形的. (1)若2x+7=10,则2x=10-7. 根据等式的性质____,等式两边同时 ; (2)若-3x=-18,则x= . 根据等式的性质____,等式两边同时____________________. (3)若3(x-2)=-6,则x-2= . 根据等式的性质____,等式两边同时 ,所以x= . 六、板书设计 §2.4等式的基本性质 等式的基本性质1: 等式的基本性质2: 例1、 七、作业布置:课本P84 练习 1、2 八、教学反思 3查看更多