- 2021-04-13 发布 |
- 37.5 KB |
- 3页

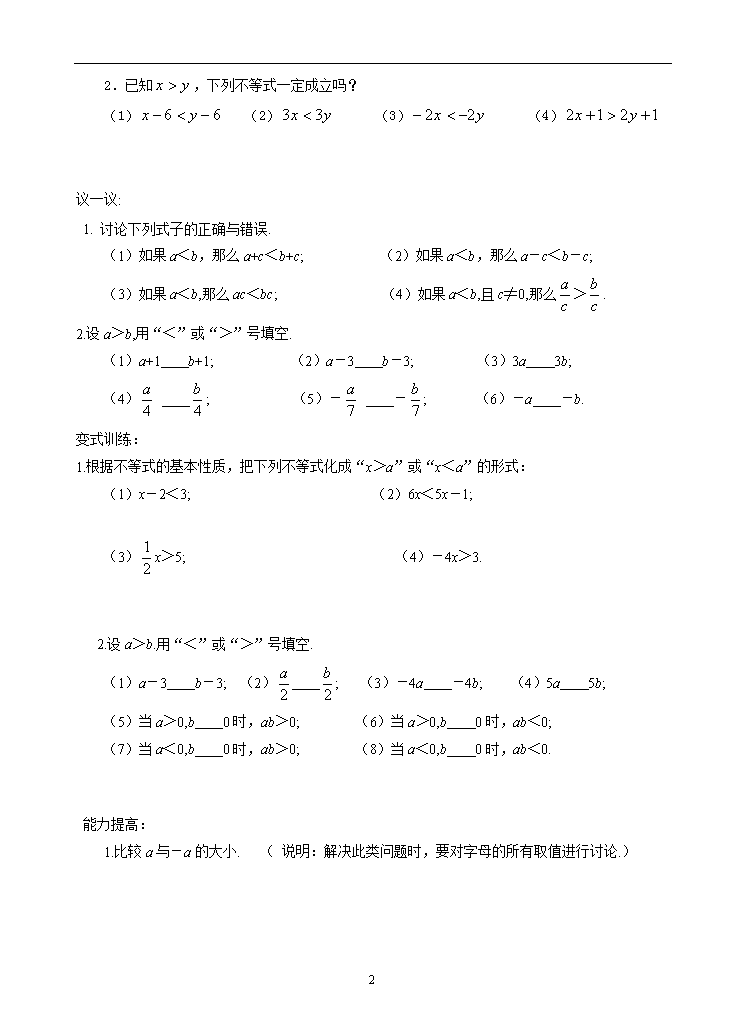

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
不等式的基本性质导学案2
2.2 不等式的基本性质 学习目标: 1.探索并掌握不等式的基本性质; 2.理解不等式与等式性质的联系与区别. 3.通过对比不等式的性质和等式的性质,培养学生的求异思维,提高大家的辨别能力. 学习重点: 探索不等式的基本性质,并能灵活地掌握和应用. 学习难点: 能根据不等式的基本性质进行化简. 回顾等式的基本性质: 等式的基本性质1:在等式的两边都加上(或减去)同一个数或整式,所得的结果仍是等式. 基本性质2:在等式的两边都乘以或除以同一个数(除数不为0),所得的结果仍是等式. 预习作业:学习教材P40-P41的内容,通过学习弄清以下问题: 1. 不等式的基本性质有哪些? 不等式的基本性质1: 不等式的两边都加上(或减去)同一个整式,不等号的方向__________ 不等式的基本性质2: 不等式的两边都乘以(或除以)同一个正数,不等号的方向____ 不等式的基本性质3: 不等式的两边都乘以(或除以)同一个负数,不等号的方向____ 2. 不等式的基本性质与等式的基本性质有什么异同? 例1、将下列不等式化成“x>a”或“x<a”的形式: (1)x-5>-1; (2)-2x>3; (3)3x<-9. (4) (5) (6) 说明:在不等式两边同时乘以或除以同一个数(除数不为0)时,要注意数的正、负,从而决定不等号方向的改变与否. 3 2.已知,下列不等式一定成立吗? (1) (2) (3) (4) 议一议: 1. 讨论下列式子的正确与错误. (1)如果a<b,那么a+c<b+c; (2)如果a<b,那么a-c<b-c; (3)如果a<b,那么ac<bc; (4)如果a<b,且c≠0,那么>. 2.设a>b,用“<”或“>”号填空. (1)a+1 b+1; (2)a-3 b-3; (3)3a 3b; (4) ; (5)- -; (6)-a -b. 变式训练: 1.根据不等式的基本性质,把下列不等式化成“x>a”或“x<a”的形式: (1)x-2<3; (2)6x<5x-1; (3)x>5; (4)-4x>3. 2.设a>b.用“<”或“>”号填空. (1)a-3 b-3; (2) ; (3)-4a -4b; (4)5a 5b; (5)当a>0,b 0时,ab>0; (6)当a>0,b 0时,ab<0; (7)当a<0,b 0时,ab>0; (8)当a<0,b 0时,ab<0. 能力提高: 1.比较a与-a的大小. ( 说明:解决此类问题时,要对字母的所有取值进行讨论.) 3 2.有一个两位数,个位上的数字是a,十位上的数是b,如果把这个两位数的个位与十位上的数对调,得到的两位数大于原来的两位数,那么a与b哪个大哪个小? 3查看更多