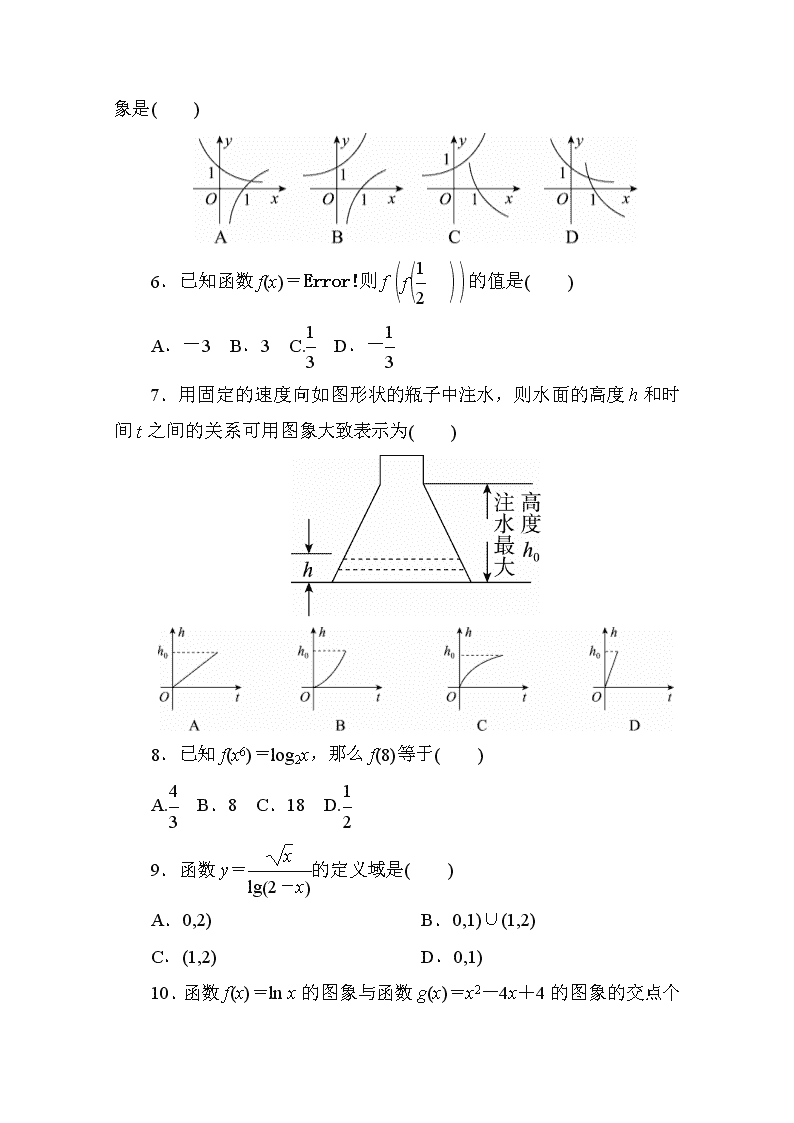高中人教a版数学必修1单元测试:创优单元测评(第一章第二章)b卷word版含解析
高中同步创优单元测评
B 卷 数 学
班级:________ 姓名:________ 得分:________
创优单元测评
(第一章 第二章)
名校好题·能力卷]
(时间:120 分钟 满分:150 分)
第Ⅰ卷 (选择题 共 60 分)
一、选择题(本大题共 12 个小题,每小题 5 分,共 60 分,在每小
题给出的四个选项中,只有一项是符合题目要求的)
1.80-lg 100 的值为( )
A.2 B.-2 C.-1 D.1
2
2.已知 f(x)=x1
2
,若 0
0 且 a≠1)( )
A.loga5.10.93.1 D.log32.90, 则 f f
1
2 的值是( )
A.-3 B.3 C.1
3 D.-1
3
7.用固定的速度向如图形状的瓶子中注水,则水面的高度 h 和时
间 t 之间的关系可用图象大致表示为( )
8.已知 f(x6)=log2x,那么 f(8)等于( )
A.4
3 B.8 C.18 D.1
2
9.函数 y= x
lg2-x
的定义域是( )
A.0,2) B.0,1)∪(1,2)
C.(1,2) D.0,1)
10.函数 f(x)=ln x 的图象与函数 g(x)=x2-4x+4 的图象的交点个
数为( )
A.0 B.1 C.2 D.3
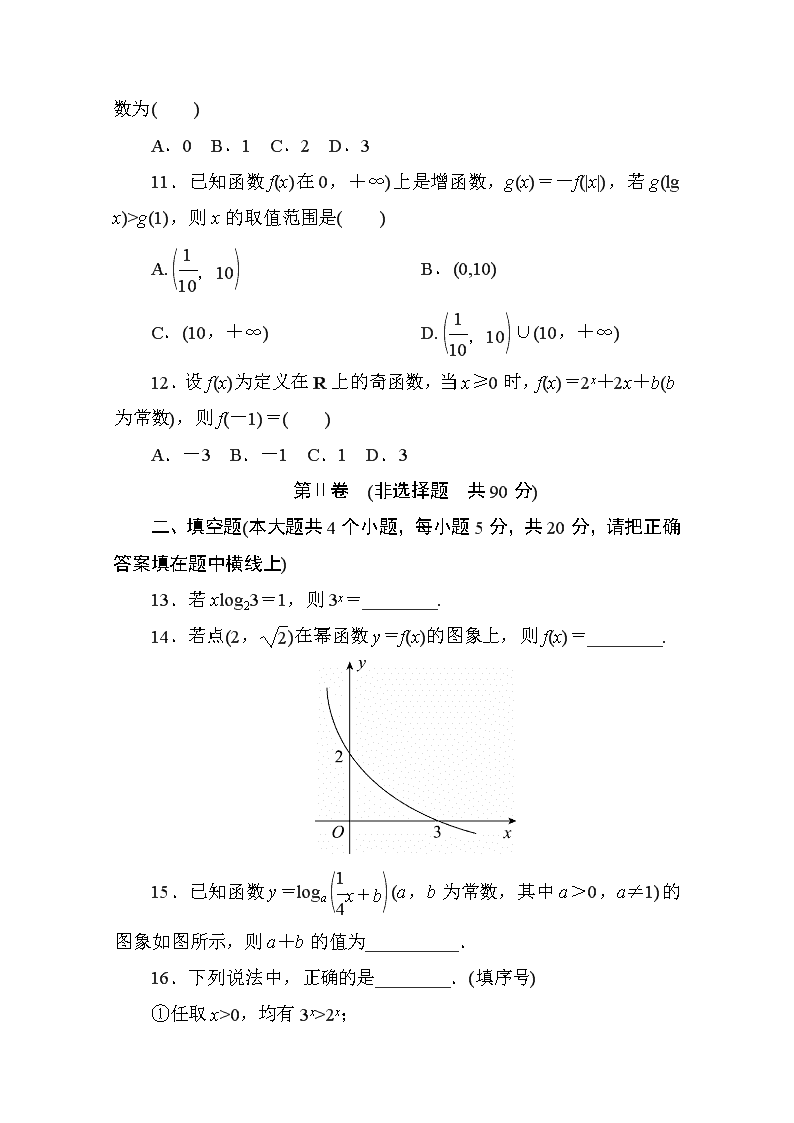
11.已知函数 f(x)在 0,+∞)上是增函数,g(x)=-f(|x|),若 g(lg
x)>g(1),则 x 的取值范围是( )
A.
1
10
,10 B.(0,10)
C.(10,+∞) D.
1
10
,10 ∪(10,+∞)
12.设 f(x)为定义在 R 上的奇函数,当 x≥0 时,f(x)=2x+2x+b(b
为常数),则 f(-1)=( )
A.-3 B.-1 C.1 D.3
第Ⅱ卷 (非选择题 共 90 分)
二、填空题(本大题共 4 个小题,每小题 5 分,共 20 分,请把正确
答案填在题中横线上)
13.若 xlog23=1,则 3x=________.
14.若点(2, 2)在幂函数 y=f(x)的图象上,则 f(x)=________.
15.已知函数 y=loga
1
4x+b (a,b 为常数,其中 a>0,a≠1)的图
象如图所示,则 a+b 的值为__________.
16.下列说法中,正确的是________.(填序号)
①任取 x>0,均有 3x>2x;
②当 a>0 且 a≠1 时,有 a3>a2;
③y=( 3)-x 是增函数;
④y=2|x|的最小值为 1;
⑤在同一坐标系中,y=2x 与 y=2-x 的图象关于 y 轴对称.
三、解答题(本大题共 6 个小题,共 70 分,解答时应写出必要的文
字说明、证明过程或演算步骤)
17.(本小题满分 12 分)
计算下列各式的值:
(1)(3 2× 3)6+( 2× 2)
4
3 -(-2 012)0;
(2)lg 5×lg 20+(lg 2)2.
18.(本小题满分 12 分)
设 f(x)=a- 2
2x+1
,x∈R.(其中 a 为常数)
(1)若 f(x)为奇函数,求 a 的值;
(2)若不等式 f(x)+a>0 恒成立,求实数 a 的取值范围.
19.(本小题满分 12 分)
已知函数 f(x)=lg(2+x),g(x)=lg(2-x),设 h(x)=f(x)+g(x).
(1)求函数 h(x)的定义域;
(2)判断函数 h(x)的奇偶性,并说明理由.
20.(本小题满分 14 分)
已知函数 f(x)=log2|x|.
(1)求函数 f(x)的定义域及 f(- 2)的值;
(2)判断函数 f(x)的奇偶性;
(3)判断 f(x)在(0,+∞)上的单调性,并给予证明.
21.某种产品的成本 f1(x)与年产量 x 之间的函数关系的图象是顶
点在原点的抛物线的一部分(如图 1),该产品的销售单价 f2(x)与年销售
量之间的函数关系图象(如图 2),若生产出的产品都能在当年销售完.
(1)求 f1(x),f2(x)的解析式;
(2)当年产量多少吨时,所获利润最大,并求出最大值.
22.(本小题满分 12 分)
设 f(x)=-2x+m
2x+1+n (m>0,n>0).
(1)当 m=n=1 时,证明:f(x)不是奇函数;
(2)设 f(x)是奇函数,求 m 与 n 的值;
(3)在(2)的条件下,求不等式 f(f(x))+f
1
4 <0 的解集.
详解答案
创优单元测评
(第一章 第二章)
名校好题·能力卷]
1.C 解析:80-lg 100=1-2=-1.
2.C 解析:∵01 有关,排除;选项
C 既不同底数又不同指数,故取“1”比较,1.70.3>1.70=1,0.93.1<0.90=1,
所以 1.70.3>0.93.1 正确.选项 D 中,log32.9>0,log0.52.2<0,D 不正确.
解题技巧:比较几个数的大小问题是指数函数、对数函数和幂函
数的重要应用,其基本方法是:将需要比较大小的几个数视为某类函
数的函数值,其主要方法可分以下三种:
(1)根据函数的单调性(如根据一次函数、二次函数、指数函数、对
数函数、幂函数的单调性),利用单调性的定义求解;
(2)采用中间量的方法(实际上也要用到函数的单调性),常用的中间
量如 0,1,-1 等;
(3)采用数形结合的方法,通过函数的图象解决.
4.A 解析:令 4x-3=1 可得 x=1,故函数 f(x)=loga(4x-3)过
定点(1,0).
5.C 解析:当 00,∴x= 2,
∴f(8)=log2 2=log22
1
2 =1
2.
9.B 解析:由题意可知,要使函数有意义,只需
x≥0,
2-x>0 且 2-x≠1, 解得 0≤x<2 且 x≠1.
∴函数 y= x
lg2-x
的定义域为 0,1)∪(1,2).
10.C 解析:g(x)=x2-4x+4=(x-2)2,在同一平面直角坐标系
内画出函数 f(x)=ln x 与 g(x)=(x-2)2 的图象(如图).由图可得两个函
数的图象有 2 个交点.
11.A 解析:因为 g(lg x)>g(1),所以 f(|lg x|)0,解得 a=1
2
,b=1
4
,
a+b=3
4.
16.①④⑤ 解析:对于①,可知任取 x>0,3x>2x 一定成立.
对于②,当 00 恒成立,
即 2a> 2
2x+1
恒成立.
因为 2x+1>1,所以 0< 2
2x+1<2,
所以 2a≥2,即 a≥1.
故 a 的取值范围是 1,+∞).
19.解:(1)∵h(x)=f(x)+g(x)=lg(x+2)+lg(2-x),
要使函数 h(x)有意义,则有 x+2>0,
2-x>0, 解得-20,解得 x≠0,
所以函数 f(x)的定义域为(-∞,0)∪(0,+∞).
f(- 2)=log2|- 2|=log22
1
2 =1
2.
(2)设 x∈(-∞,0)∪(0,+∞),则-x∈(-∞,0)∪(0,+∞).
f(-x)=log2|-x|=log2|x|=f(x),
所以 f(-x)=f(x),
所以函数 f(x)是偶函数.
(3)f(x)在(0,+∞)上是单调增函数.证明如下:
设 x1,x2∈(0,+∞),且 x1-1
4
,2x<3,得 x0 的解集为(-∞,log23).