- 2021-04-14 发布 |
- 37.5 KB |
- 18页

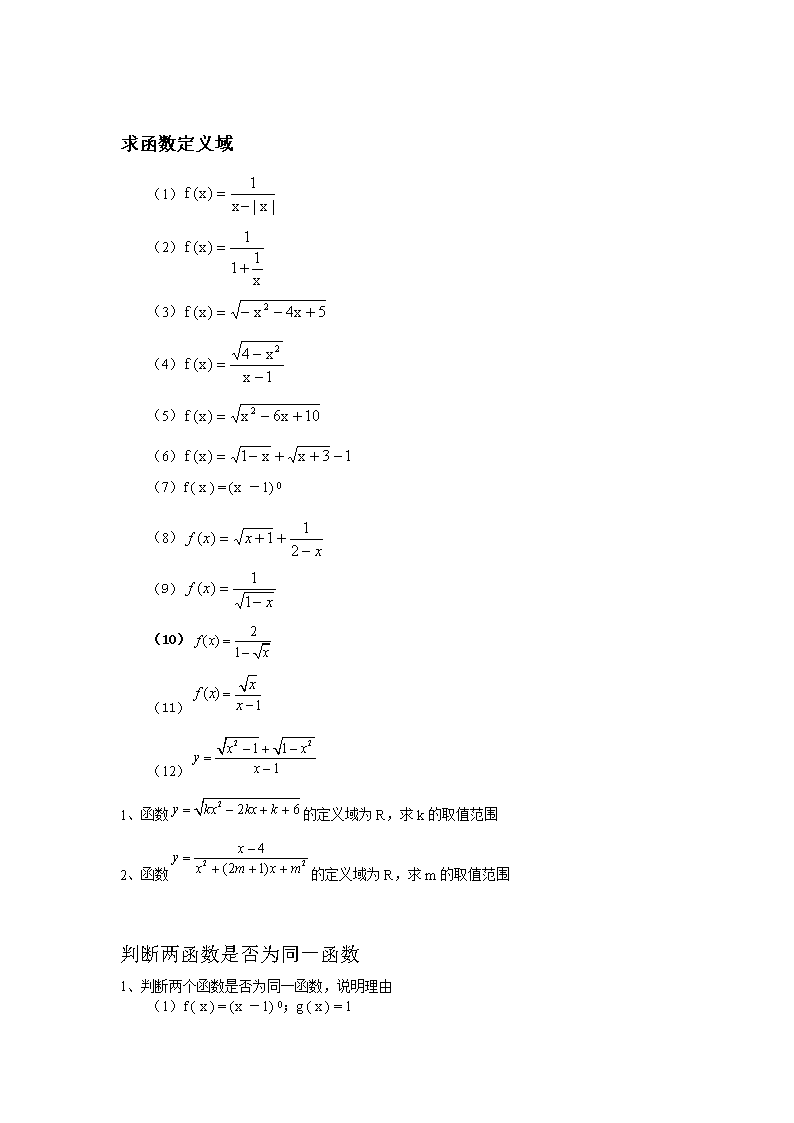

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修1函数题型分析(精心整理版)
2.1 函数的概念 (一)函数的概念 设 A、B 是非空的数集,如果按照某个确定的对应关系 f,使对于集合 A 中的任意一个 数 x,在集合 B 中都有唯一确定的数 f(x)和它对应,那么就称 f:A→B 为从集合 A 到集合 B 的一个函数. 记作: y=f(x),x∈A.(y 就是 x 在 f 作用下的对应值) 其中,x 叫做自变量,x 的取值范围 A 叫做函数的定义域;与 x 的值相对应的 y 值叫做 函数值,函数值的集合{f(x)| x∈A }叫做函数的值域. (二)构成函数的三要素: 定义域、对应关系和值域 判断两变量之间是否是函数关系 (1)定义域与对应关系是否给出, (2)根据给出的对应法则,自变量 x 在其定义域中的每一个值,是否都能确定唯一的 函数值。 (三)区间的概念 (1)区间的分类:开区间、闭区间、半开半闭区间;(a,b 为端点) 满足 a x b 的全体实数 x 的集合叫做闭区间,记作 ,a b 满足 a x b 的全体实数 x 的集合叫做开区间,记作 ,a b 满足 a x b 或 a x b 的全体实数 x 的集合叫做半开半闭区间,分别记作 [ , )a b 或 ( , ]a b (2)无穷区间; (3)区间的数轴表示. 函数概念 1、如下图可作为函数 )(xf 的图像的是( ) A B C D 2. 下列四个图形中,不是..以 x 为自变量的函数的图象是 x y O x y O x y O x y O A. B. C. D. 求函数定义域 (1) |x|x 1)x(f (2) x 11 1)x(f (3) 5x4x)x(f 2 (4) 1x x4)x(f 2 (5) 10x6x)x(f 2 (6) 13xx1)x(f (7)f ( x ) = (x -1) 0 (8) xxxf 2 11)( (9) x xf 1 1)( (10) 2( ) 1 f x x (11) ( ) 1 xf x x (12) 2 21 1 1 x xy x 1、函数 2 2 6y kx kx k 的定义域为 R,求 k 的取值范围 2、函数 2 2 4 (2 1) xy x m x m 的定义域为 R,求 m 的取值范围 判断两函数是否为同一函数 1、判断两个函数是否为同一函数,说明理由 (1)f ( x ) = (x -1) 0;g ( x ) = 1 (2)f ( x ) = x; g ( x ) = 2x (3)f ( x ) = x 2;f ( x ) = (x + 1) 2 (4)f ( x ) = | x | ;g ( x ) = 2x 2、判断两个函数是否为同一函数,说明理由 (1) ( 3)( 5) 3 x xy x ; 5y x (2) 1 1y x x ; ( 1)( 1)y x x (3) 3 4 3y x x ; 3 1y x x (4) 11y x ; 11u v 求函数解析式 (1)代入法 1、 已知函数 2( ) 1f x x ,求 ( )f x , (1 )f x 2、 已知函数 )31(12)( xxxf ,则 ( ) A. )1( xf = )20(22 xx B. )1( xf = )42(12 xx C. )1( xf = )20(22 xx D. )1( xf = )42(12 xx 3、 已知 2( )f x x m , ( ) ( ( ))g x f f x ,求 ( )g x 的解析式。 (2)换元法 1、已知 2( 1)f xx ,求 ( )f x ; 2、已知函数 2( 1)f x x ,求 ( )f x 3、 若 1( ) 1 xf x x ,求 ( ).f x 4、若 ( 1) 2f x x x ,求 ( ).f x 5. 已知ƒ( x +1)=x+1,则函数ƒ(x)的解析式为 A.ƒ(x)=x2 B.ƒ(x)=x2+1 C.ƒ(x)=x2-2x+2 D.ƒ(x)=x2-2x 6.已知 2)1( xxf ,则 ( )f x 的表达式为 ( ) A. 2( ) 2 1f x x x B. 2( ) 2 1f x x x C. 2( ) 2 1f x x x D. 2( ) 2 1f x x x 9、设函数 ( ) 2 1f x x ,则方程 (2 1)f x x 的解为 7. 已知 )0(1)21( 2 2 x x xxf ,则 )2 1(f 的值为____________________。 8.已知 f(2x-1)=x2,则 f(5)=______.9 (3)待定系数法 1、若 )(xf 是一次函数, 14)]([ xxff 且,则 )(xf = _________________. 2、已知 ( )f x 是一次函数,且满足 3 ( 1) 2 ( 1) 2 17f x f x x ,求 ( )f x ; 分段函数 函数图像 1. 已知函数解析法可表示为 , 0,1 2 , 1,2 x x y x x ,用图像表示这个函数。 2. 把下列函数分区间表示,并作出函数的图像 (1) 1 | |y x (2) 3 | |y x (3) | 1| | 4 |y x x (4) 2 2 2 (0 3)( ) 6 ( 2 0) x x xf x x x x (5) ,< ,+ )2(2 )2(22 xx xx (6) 2 2 ( 1) ( ) ( 1 2) 2 ( 2) x x f x x x x x ≤ ≥ (7) 2( 1) , , 1 2 2, 1,1 1 1, 1, x x y x x xx 求函数值 1. 作函数 2 , 1 0 ,0 1 ,1 2 x x y x x x x 的图像,并求 1 1( 0.8), ( ), ( )2 3f f f 2、设函数 3,( 10)( ) ( ( 5)),( 10) x xf x f f x x ,则 (5)f =_____ 3、已知函数 3, 10, , 85 , 10, x x f x x N ff f x x 其中 则 ( ) A.2 B.4 C.6 D.7 4、已知 1, 1 3, 1 x xf x x x ,那么 1 2f f 的值是 ( B ) A. 2 5 B. 2 3 C. 2 9 D. 2 1 5.已知 f(x)= )0x(0 )0x( )0x(1x ,则 f [f(-2)]=________________. 6、已知,则 2 , 0, , 0, 3 0, 0. x x f x x f f f x 那么 的值等于 ( ) A.0 B. C. 2x D.9 7. 定义在 R 上的函数 ( )f x 满足 12 , 0,( ) ( 1) ( 2), 0. x xf x f x f x x 则 ( 1)f ______, (33)f ______. 4 2 给出函数值求自变量的值 1、设函数 f(x)= ,< ,+ )2(2 )2(22 xx xx 则 f(-4)=____,又知 f( 0x )=8,则 0x =____ 2、设 2 2 ( 1) ( ) ( 1 2) 2 ( 2) x x f x x x x x ≤ ≥ ,若 ( ) 3f x ,则 x=____________。 3、函数 y= 1)( 5- 1),(0 3 0),( 32 xx xx xx 的最大值是_______. 4. 已知 2 1 )( x x xf ),0( ),0( ),0( x x x 如果 3)( 0 xf ,那么 0x ____________。 5.已知函数 x xxf 4 )( 2 )1( )1( x x 若 9)( xf ,则 x = . 6 、 设 函 数 2( 1) .( 1)( ) 4 1.( 1) x xf x x x , 则 使 得 ( ) 1f x 的 自 变 量 x 的 取 值 范 围 是 __________; 7、 已知 1 ( 0)( ) 1 ( 0) xf x x ,则不等式 ( 2) ( 2) 5x x f x 的解集是________ 8、 已知 0,1 0,1)( x xxf ,则不等式 4)2()12( xfxx 的解集是 【-5,1】 函数单调性 单调性概念考察 1. 若函数 )(xf 在区间(a,b)上为增函数,在区间(b,c)上也是增函数,则函数 )(xf 在 区间(a,c)上( ) (A)必是增函数 (B)必是减函数 (C)是增函数或是减函数(D)无法确定增减性 2.函数 )(xf 在 ),( ba 和 ),( dc 都是增函数,若 ),(),,( 21 dcxbax ,且 21 xx 那么( ) A. )()( 21 xfxf B. )()( 21 xfxf C. )()( 21 xfxf D.无法确定 3.已知函数 y=f(x)在 R 上是增函数,且 f(2m+1)>f(3m-4),则 m 的取值范围是( ) A.(-∞,5) B.(5,+∞) C. ),5 3( D. )5 3,( 4 . 函 数 ( )f x 的 定 义 域 为 ),( ba , 且 对 其 内 任 意 实 数 1 2,x x 均 有 : 1 2 1 2( )[ ( ) ( )] 0x x f x f x ,则 ( )f x 在 ),( ba 上是( ) (A)增函数 (B)减函数 (C)奇函数 (D)偶函数 5. 函数 f(x)在(0,+∞)上为减函数,那么 f(a2-a+1)与 )4 3(f 的大小关系是______。 6.已知函数 f(x)在区间[a,b]上单调,且 f(a)f(b)<0,则方程 f(x)=0 在区间[a,b]内( ) A.至少有一实根 B.至多有一实根 C.没有实根 D.必有唯一的实根 7.当 时,函数 的值有正也有负,则实数 a 的取值范围是 () A. B. C. D. 8. 已知函数 f(x)在其定义域 D 上是单调函数,其值域为 M,则下列说法中 ①若 x0∈D,则有唯一的 f(x0)∈M ②若 f(x0)∈M,则有唯一的 x0∈D ③对任意实数 a,至少存在一个 x0∈D,使得 f(x0)=a ④对任意实数 a,至多存在一个 x0∈D,使得 f(x0)=a 错误的个数是( ) A.1 个 B.2 个 C.3 个 D.4 个 9.已知f(x)在区间(-∞,+∞)上是增函数,a、b∈R 且a+b≤0,则下列不等式中正确的是( ) A.f(a)+f(b)≤-f(a)+f(b)] B.f(a)+f(b)≤f(-a)+f(-b) C.f(a)+f(b)≥-f(a)+f(b)] D.f(a)+f(b)≥f(-a)+f(-b) 10.已知 f(x)是定义在(-2,2)上的减函数,并且 f(m-1)-f(1-2m)>0,求实数 m 的取值 范围. 解析: ∵f(x)在(-2,2)上是减函数 ∴由 f(m-1)-f(1-2m)>0,得 f(m-1)>f(1-2m) ∴ 3 2 2 3 2 1 31 211 ,2212 212 m m m mm m m 即 解得 3 2 2 1 m ,∴m 的取值范围是(- 3 2,2 1 ) 11. 已知:f(x)是定义在[-1,1]上的增函数,且 f(x-1)查看更多