备战2014高考数学 高频考点归类分析（真题为例）：反函数

备战2014高考数学 高频考点归类分析（真题为例）：反函数

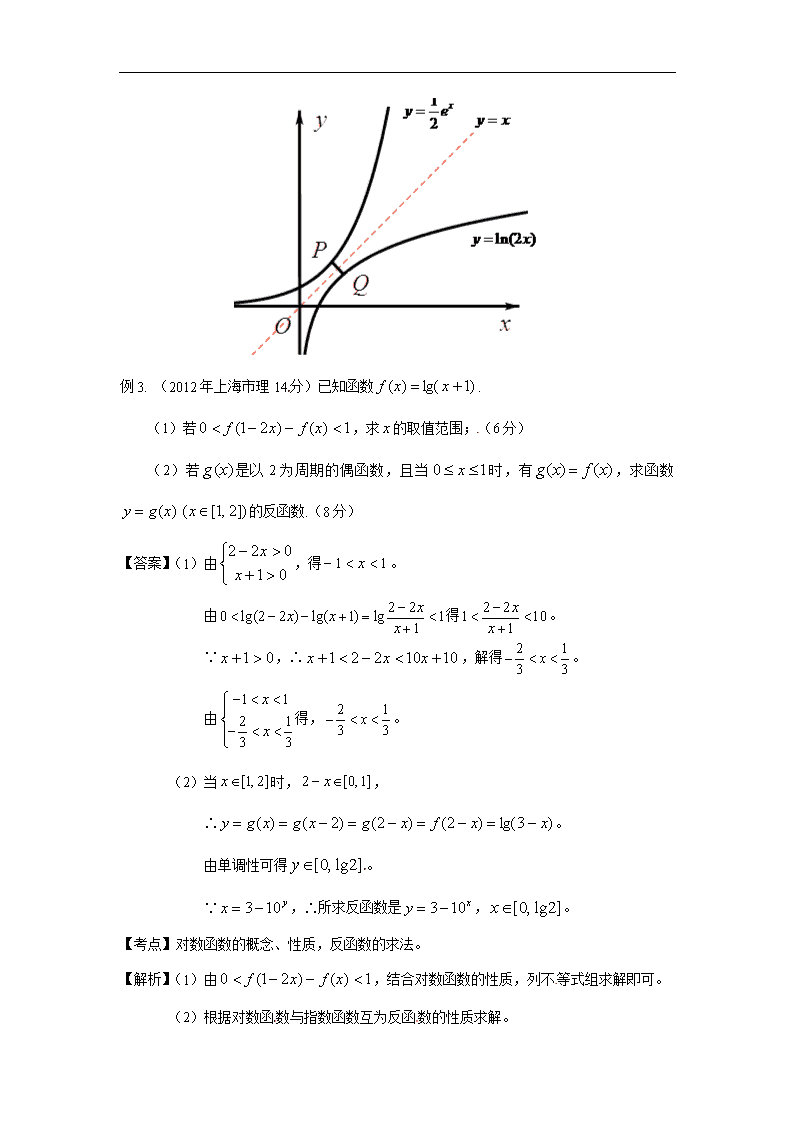
反函数问题 典型例题： ‎ 例1. （2012年全国大纲卷文5分）函数= (≥－1)的反函数为【 】‎ A. B. C. D. ‎ ‎【答案】A。‎ ‎【考点】反函数。[来源:Z&xx&k.Com][来源:学科网]‎ ‎【解析】由原函数求出关于的关系式，再、对换，原函数的值域是反函数的定义域。因此，‎ ‎ 将=两边平方，得，即。将、对换，得。‎ ‎ 又函数=的值域为，所以的定义域为。故选A。‎ 例2. （2012年全国课标卷理5分）设点在曲线上，点在曲线上，则最小值为【 】‎ ‎ [来源:学。科。网Z。X。X。K]‎ ‎【答案】。‎ ‎【考点】反函数的性质，导数的应用。‎ ‎【解析】∵函数与函数互为反函数，∴它们的图象关于对称。‎ ‎ ∴函数上的点到直线的距离为 ‎ 设函数，则，∴。∴。‎ ‎ ∴由图象关于对称得：最小值为。故选。[来源:Zxxk.Com]‎ 例3. （2012年上海市理14分）已知函数.[来源:学科网]‎ ‎ （1）若，求的取值范围；（6分）‎ ‎ （2）若是以2为周期的偶函数，且当时，有，求函数的反函数.（8分）‎ ‎【答案】（1）由，得。‎ ‎ 由得。‎ ‎ ∵，∴，解得。‎ ‎ 由得，。‎ ‎ （2）当时，，‎ ‎∴。‎ 由单调性可得。‎ ‎∵，∴所求反函数是，。‎ ‎【考点】对数函数的概念、性质，反函数的求法。‎ ‎【解析】（1）由，结合对数函数的性质，列不等式组求解即可。‎ ‎（2）根据对数函数与指数函数互为反函数的性质求解。‎