2014年高考数学(理科)真题分类汇编I单元 统计
数 学
I单元 统计
I1 随机抽样
2.I1[2014·湖南卷] 对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为p1,p2,p3,则( )
A.p1=p2<p3 B.p2=p3<p1
C.p1=p3<p2 D.p1=p2=p3
2.D [解析] 不管是简单随机抽样、系统抽样还是分层抽样,它们都是等概率抽样,每个个体被抽中的概率均为.
9.I1[2014·天津卷] 某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4∶5∶5∶6,则应从一年级本科生中抽取________名学生.
9.60 [解析] 由分层抽样的方法可得,从一年级本科生中抽取学生人数为300×=60.
I2 用样本估计总体
6.I2[2014·广东卷] 已知某地区中小学生人数和近视情况分别如图11和图12所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
图11 图12
A.200,20 B.100,20
C.200,10 D.100,10
6.A [解析] 本题考查统计图表的实际应用.根据图题中的图知该地区中小学生一共有10 000人,由于抽取2%的学生,所以样本容量是10 000×2%=200.由于高中生占了50%,所以高中生近视的人数为2000×2%×50%=20.
17.I2、K5[2014·广东卷] 随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.
根据上述数据得到样本的频率分布表如下:
分组
频数
频率
[25,30]
3
0.12
(30,35]
5
0.20
(35,40]
8
0.32
(40,45]
n1
f1
(45,50]
n2
f2
(1)确定样本频率分布表中n1,n2,f1和f2的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率.
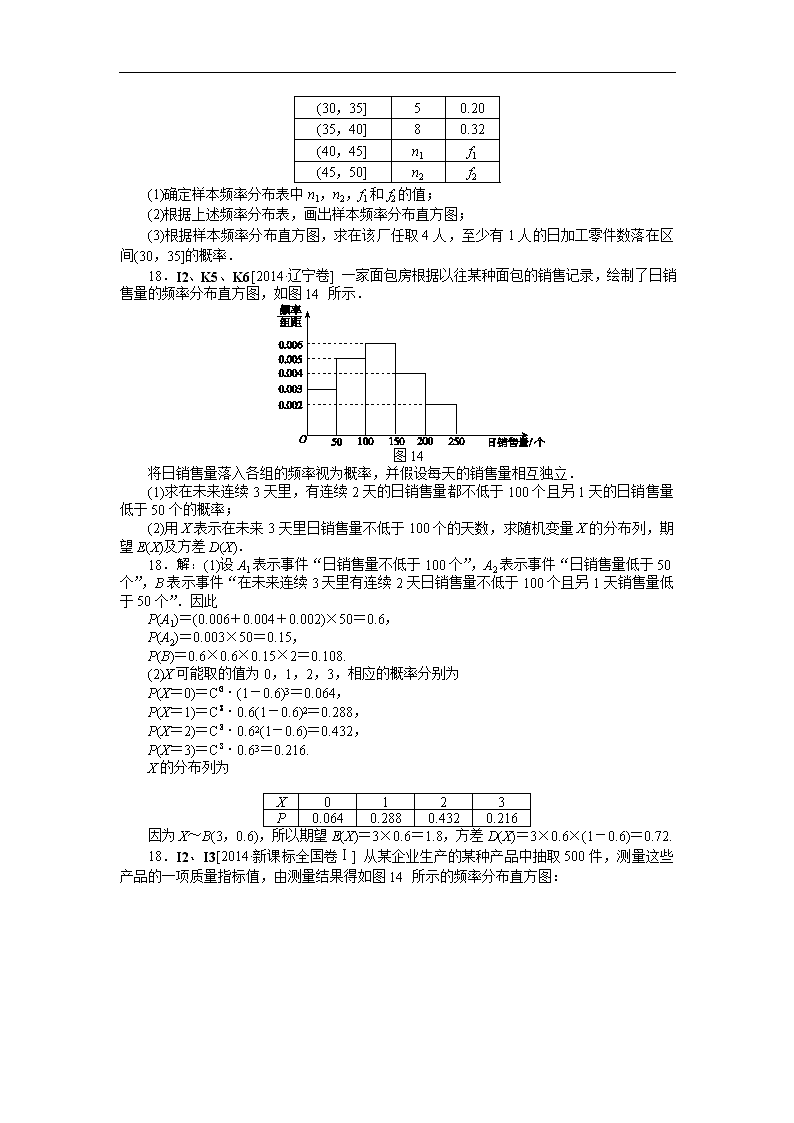
18.I2、K5、K6[2014·辽宁卷] 一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图14所示.
图14
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X).
18.解:(1)设A1表示事件“日销售量不低于100个”,A2表示事件“日销售量低于50个”,B表示事件“在未来连续3天里有连续2天日销售量不低于100个且另1天销售量低于50个”.因此
P(A1)=(0.006+0.004+0.002)×50=0.6,
P(A2)=0.003×50=0.15,
P(B)=0.6×0.6×0.15×2=0.108.
(2)X可能取的值为0,1,2,3,相应的概率分别为
P(X=0)=C·(1-0.6)3=0.064,
P(X=1)=C·0.6(1-0.6)2=0.288,
P(X=2)=C·0.62(1-0.6)=0.432,
P(X=3)=C·0.63=0.216.
X的分布列为
X
0
1
2
3
P
0.064
0.288
0.432
0.216
因为X~B(3,0.6),所以期望E(X)=3×0.6=1.8,方差D(X)=3×0.6×(1-0.6)=0.72.
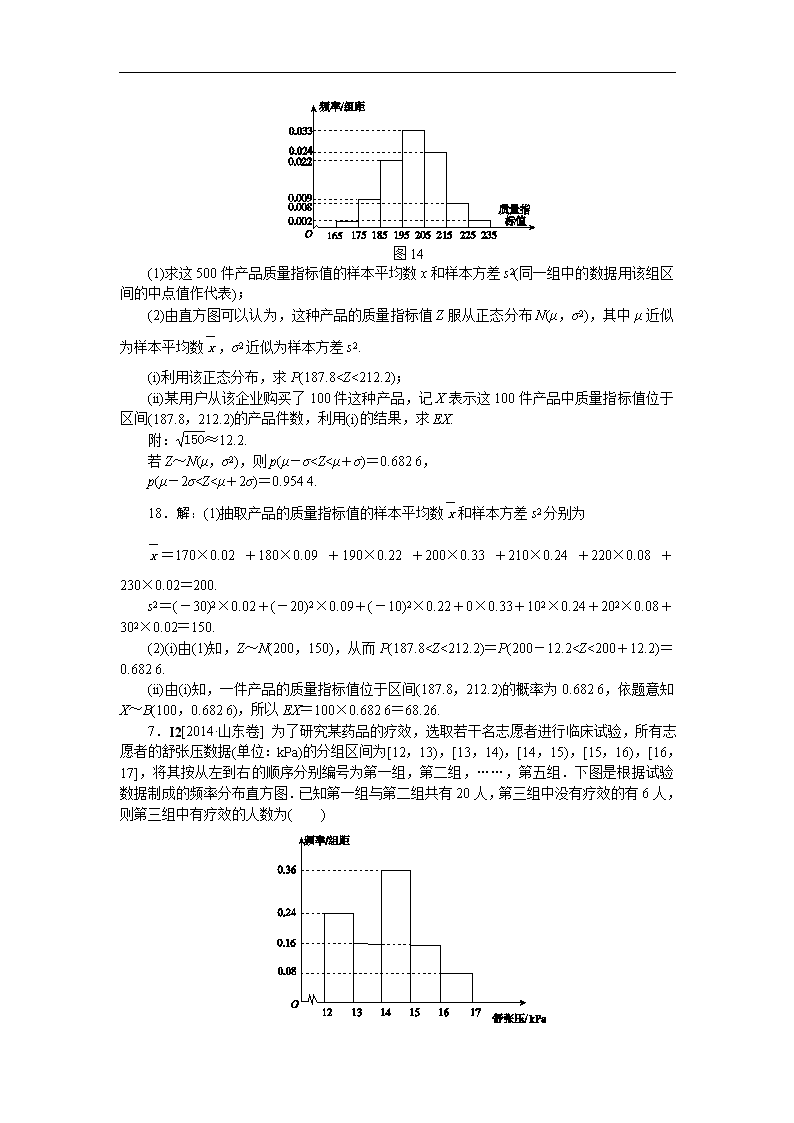
18.I2、I3[2014·新课标全国卷Ⅰ] 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如图14所示的频率分布直方图:
图14
(1)求这500件产品质量指标值的样本平均数x和样本方差s2(同一组中的数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数,σ2近似为样本方差s2.
(i)利用该正态分布,求P(187.8
0,b>0 B.a>0,b<0
C.a<0,b>0 D.a<0,b<0
4.B [解析] 作出散点图如下:
观察图象可知,回归直线=bx+a的斜率b<0,截距a>0.故a>0,b<0.故选B.
6.I4[2014·江西卷] 某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )
表1 表2
成绩
性别
不及格
及格
总计
男
6
14
20
女
10
22
32
总计
16
36
52
视力
好
差
总计
性别
男
4
16
20
女
12
20
32
总计
16
36
52
表3 表4
智商
性别
偏高
正常
总计
男
8
12
20
女
8
24
32
总计
16
36
52
阅读量
性别
丰富
不丰
富
总计
男
14
6
20
女
2
30
32
总计
16
36
52
A.成绩 B.视力 C.智商 D.阅读量
6.D [解析] 根据独立性检验计算可知,阅读量与性别有关联的可能性较大.
19.I4[2014·新课标全国卷Ⅱ] 某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年份
2007
2008
2009
2010
2011
2012
2013
年份代号t
1
2
3
4
5
6
7
人均纯收入y
2.9
3.3
3.6
4.4
4.8
5.2
5.9
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
19.解:(1)由所给数据计算得=(1+2+3+4+5+6+7)=4,=(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
=-=4.3-0.5×4=2.3,
所求回归方程为=0.5t+2.3.
(2)由(1)知,=0.5>0,故2007年至2013年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2015年的年份代号t=9,代入(1)中的回归方程,得=0.5×9+2.3=6.8,
故预测该地区2015年农村居民家庭人均纯收入为6.8千元.
I5 单元综合
2.[2014·福州期末] 将参加夏令营的500名学生分别编号为001,002,…,500,这500名学生分住在三个营区,从001到200在第一营区,从201到350在第二营区,从351到500在第三营区.若采用分层抽样的方法抽取一个容量50的样本,则三个营区被抽取的人数分别为( )
A.20,15,15 B.20,16,14
C.12,14,16 D.21,15,14
2.A [解析] 根据分层抽样的比例抽取,分别应抽取的人数为20,15,15.
3.[2014·广州调研] 如图X381所示是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
图X381
A.85,84 B.84,85
C.86,84 D.84,86
3.A [解析] 由题意可知,所剩数据的平均数为x==85,众数为84.
4.[2014·泰安一模] 为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老人,其结果如下表:
性别
是否需要
志愿者
男
女
需要
40
30
不需要
160
270
由K2=,得
K2=≈9.967.
附表:
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
参照附表,可得到的结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“需要志愿者提供帮助与性别无关”
C.有99%以上的把握认为“需要志愿者提供帮助与性别有关”
D.有99%以上的把握认为“需要志愿者提供帮助与性别无关”
4.C [解析] 由数据知,选项C正确.
6.[2014·威海一模] 某班级统计一次数学测试后的成绩,并制成了如下的频率分布表,根据该表估计该班级的数学测试平均分为( )
分组
[60,70)
[70,80)
[80,90)
[90,100]
人数
5
15
20
10
频率
0.1
0.3
0.4
0.2
A.80 B.81 C.82 D.83
6.C [解析] 65×0.1+75×0.3+85×0.4+95×0.2=82.
8.[2014·邯郸期末] 某商场在庆元宵促销活动中,对元宵节当天9时至14时的销售额进行统计,其频率分布直方图如图X382所示.已知9时至10时的销售额为2.5万元,则11时至12时的销售额为________万元.
图X382
8.10 [解析] 设11时至12时的销售额为x万元,则=,解得x=10.
11.[2014·韶关一模] 设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为=0.85x-85.71,给出下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本点的中心(x,y);
③若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
④若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg.
其中,正确结论的序号是______________.
11.①②③ [解析] 利用有关概念可知,①②③正确.