- 2021-04-19 发布 |
- 37.5 KB |
- 16页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北京市大兴区2019~2020学年度第二学期期末检测试卷高一数学 (解析版)
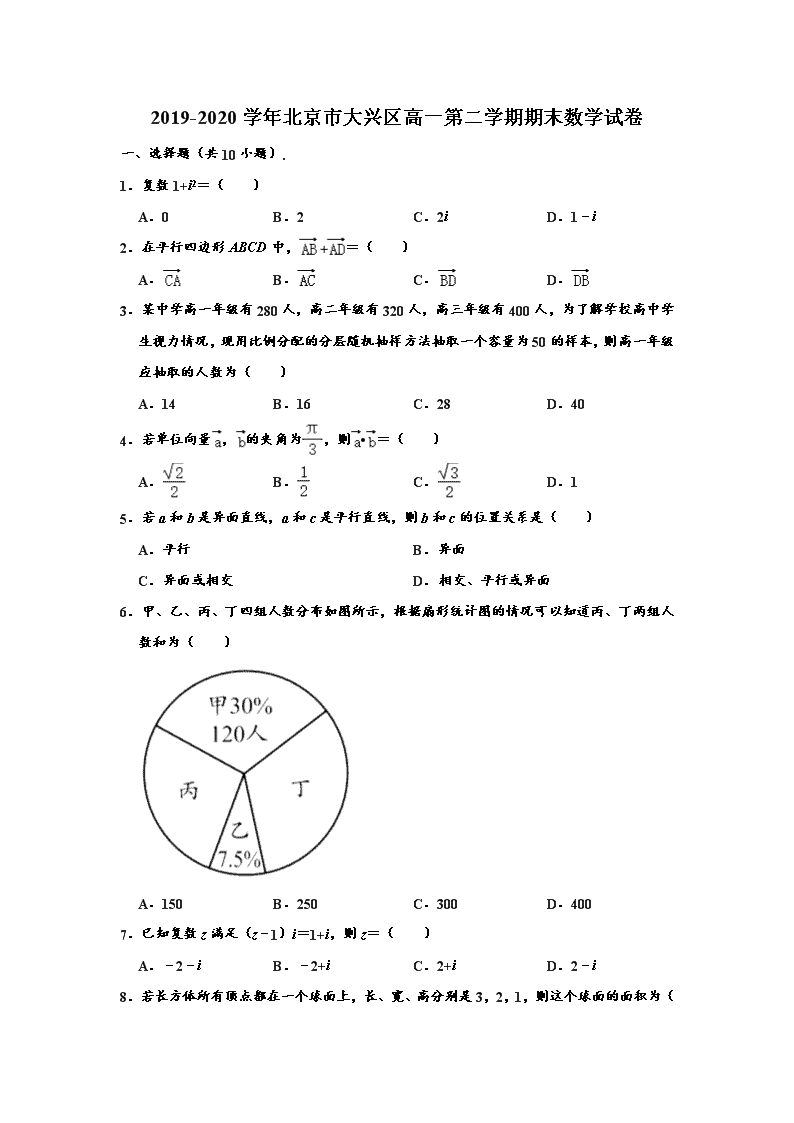
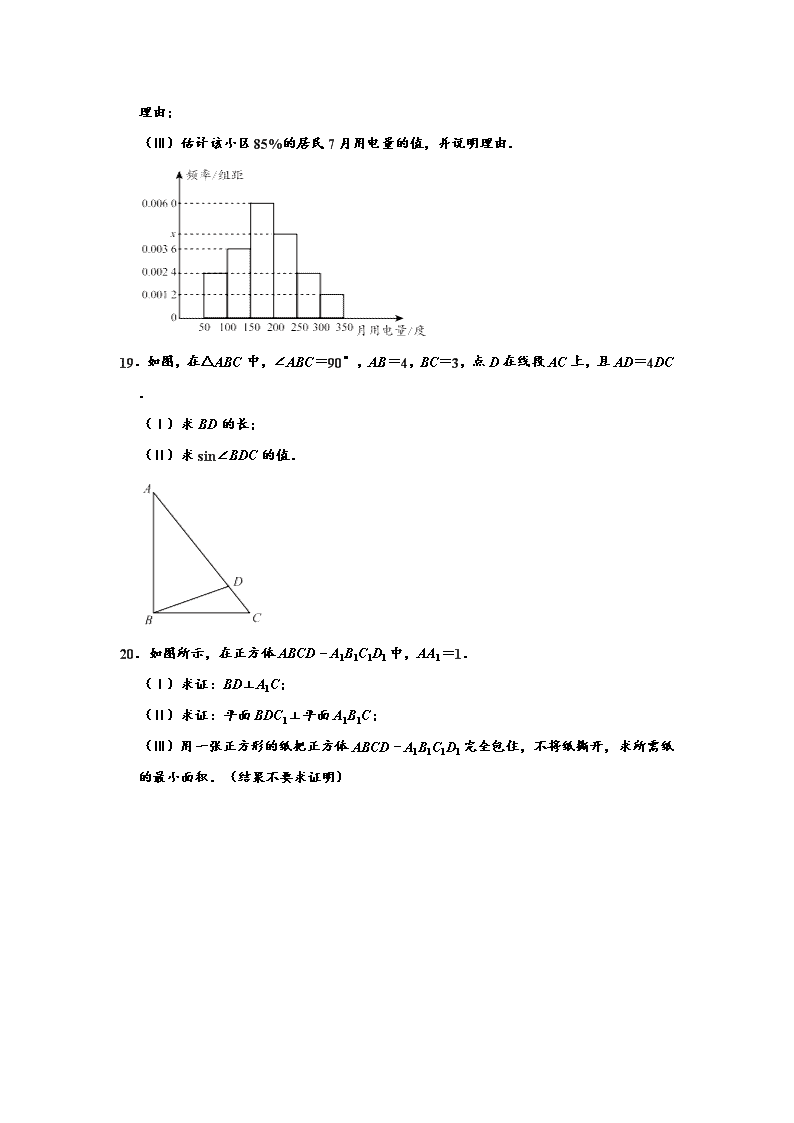
2019-2020学年北京市大兴区高一第二学期期末数学试卷 一、选择题(共10小题). 1.复数1+i2=( ) A.0 B.2 C.2i D.1﹣i 2.在平行四边形ABCD中,=( ) A. B. C. D. 3.某中学高一年级有280人,高二年级有320人,高三年级有400人,为了解学校高中学生视力情况,现用比例分配的分层随机抽样方法抽取一个容量为50的样本,则高一年级应抽取的人数为( ) A.14 B.16 C.28 D.40 4.若单位向量,的夹角为,则•=( ) A. B. C. D.1 5.若a和b是异面直线,a和c是平行直线,则b和c的位置关系是( ) A.平行 B.异面 C.异面或相交 D.相交、平行或异面 6.甲、乙、丙、丁四组人数分布如图所示,根据扇形统计图的情况可以知道丙、丁两组人数和为( ) A.150 B.250 C.300 D.400 7.已知复数z满足(z﹣1)i=1+i,则z=( ) A.﹣2﹣i B.﹣2+i C.2+i D.2﹣i 8.若长方体所有顶点都在一个球面上,长、宽、高分别是3,2,1,则这个球面的面积为( ) A.9π B.12π C.14π D.18π 9.设,为非零向量,则“|+|=||+||”是“与共线”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 10.已知△ABC是等腰三角形,AB=AC=5,BC=6,点P在线段AC上运动,则的取值范围是( ) A.[3,4] B.[,6] C.[6,8] D.[,8] 二、填空题共5小题,每小题5分,共25分. 11.设复数z=1+i,则z的模|z|= . 12.数据19,20,21,23,25,26,27,则这组数据的方差是 . 13.三棱锥的三条侧棱两两垂直,长分别为1,2,3,则这个三棱锥的体积为 . 14.已知=(1,2),=(2,y),|+|=|﹣|,则y= . 15.在△ABC中,b=10,A=. ①若a=5,则角B大小为 ; ②若角B有两个解,则a的取值范围是 . 三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。 16.已知复数z=(m2﹣m)+(m+3)i(m∈R)在复平面内对应点Z. (Ⅰ)若m=2,求z; (Ⅱ)若点Z在直线y=x上,求m的值. 17.已知三个点A(2,1),B(3,2),D(﹣1,4). (Ⅰ)求证:AB⊥AD; (Ⅱ)若四边形ABCD为矩形,求点C的坐标及矩形ABCD两对角线所成锐角的余弦值. 18.为了解某小区7月用电量情况,通过抽样,获得了100户居民7月用电量(单位:度),将数据按照[50,100),[100,150),…,[300,350]分成六组,制成了如图所示的频率分布直方图. (Ⅰ)求频率分布直方图中x的值; (Ⅱ )已知该小区有1000户居民,估计该小区7月用电量不低于200度的户数,并说明理由; (Ⅲ)估计该小区85%的居民7月用电量的值,并说明理由. 19.如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC. (Ⅰ)求BD的长; (Ⅱ)求sin∠BDC的值. 20.如图所示,在正方体ABCD﹣A1B1C1D1中,AA1=1. (Ⅰ)求证:BD⊥A1C; (Ⅱ)求证:平面BDC1⊥平面A1B1C; (Ⅲ)用一张正方形的纸把正方体ABCD﹣A1B1C1D1完全包住,不将纸撕开,求所需纸的最小面积.(结果不要求证明) 21.如图所示,在四棱锥P﹣ABCD中,BC∥平面PAD,BC=AD,E是PD的中点. (Ⅰ)求证:BC∥AD; (Ⅱ)求证:CE∥平面PAB; (Ⅲ)若M是线段CE上一动点,则线段AD上是否存在点N,使MN∥平面PAB?说明理由. 参考答案 一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.复数1+i2=( ) A.0 B.2 C.2i D.1﹣i 【分析】直接利用虚数单位i的运算性质化简求值. 解:∵i2=﹣1, ∴1+i2=1﹣1=0. 故选:A. 2.在平行四边形ABCD中,=( ) A. B. C. D. 【分析】利用向量平行四边形法则即可得出. 解:由向量平行四边形法则可得:=, 故选:B. 3.某中学高一年级有280人,高二年级有320人,高三年级有400人,为了解学校高中学生视力情况,现用比例分配的分层随机抽样方法抽取一个容量为50的样本,则高一年级应抽取的人数为( ) A.14 B.16 C.28 D.40 【分析】先求出抽取样本的比例是多少,再计算从高一学生中应抽取的人是多少. 解:根据题意,得; 抽取样本的比例是=, ∴从高一学生中应抽取的人数为280×=14. 故选:A. 4.若单位向量,的夹角为,则•=( ) A. B. C. D.1 【分析】直接利用向量的数量积求解即可. 解:单位向量,的夹角为,则•==. 故选:B. 5.若a和b是异面直线,a和c是平行直线,则b和c的位置关系是( ) A.平行 B.异面 C.异面或相交 D.相交、平行或异面 【分析】借助正方体模型,找出三条直线a,b,c,符合题意,判断b,c的位置关系. 解:考虑正方体ABCD﹣A'B'C'D'中,直线AB看做直线a,直线B'C'看做直线b, 即直线a和直线b是异面直线, 若直线CD看做直线c,可得a,c平行,则b,c异面; 若直线A'B'看做直线c,可得a,c平行,则b,c相交. 若b,c平行,由a,c平行,可得a,b平行,这与a,b异面矛盾,故b,c不平行. 故选:C. 6.甲、乙、丙、丁四组人数分布如图所示,根据扇形统计图的情况可以知道丙、丁两组人数和为( ) A.150 B.250 C.300 D.400 【分析】先根据甲组人数及其所占百分比可得总人数,再求出丙、丁两组人数占总人数的百分比,即可得解. 解:∵甲组人数为120人,占总人数的百分比为30%, ∴总人数为=120÷30%=400人, ∵丙、丁两组人数和占总人数的百分比为1﹣30%﹣7.5%=62.5% ∴丙、丁两组人数和为400×62.5%=250人. 故选:B. 7.已知复数z满足(z﹣1)i=1+i,则z=( ) A.﹣2﹣i B.﹣2+i C.2+i D.2﹣i 【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案. 解:由(z﹣1)i=1+i,得z﹣1=, ∴z=2﹣i. 故选:D. 8.若长方体所有顶点都在一个球面上,长、宽、高分别是3,2,1,则这个球面的面积为( ) A.9π B.12π C.14π D.18π 【分析】求出长方体的对角线的长度,得到外接球的直径,然后求解外接球的表面积. 解:长方体所有顶点都在一个球面上,长、宽、高分别是3,2,1, 所以长方体的外接球的直径为:=, 外接球的半径为:. 则这个球面的面积为:4×=14π. 故选:C. 9.设,为非零向量,则“|+|=||+||”是“与共线”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 【分析】结合向量数量积的性质及向量共线的定义即可求解. 解:因为,为非零向量,由|+|=||+||两边平方可得,=|||, 故夹角θ=0,即与共线, 当与共线时,夹角θ=0或π,此时|+|=||+||不一定成立. 故选:A. 10.已知△ABC是等腰三角形,AB=AC=5,BC=6,点P在线段AC上运动,则的取值范围是( ) A.[3,4] B.[,6] C.[6,8] D.[,8] 【分析】以BC的中点O为坐标原点,BC所在直线为x轴,OA所在直线为y轴建立直角坐标系,分别求得B,C,A的坐标,可得直线AC的方程,设P(m,n),(0≤n≤4),即有m=3﹣n,再由向量的运算和模的公式,可得n的函数,结合二次函数的最值求法,可得所求范围. 解:以BC的中点O为坐标原点,BC所在直线为x轴, OA所在直线为y轴建立直角坐标系, 可得B(﹣3,0),C(3,0),由|AC|=5,可得A(0,4), 直线AC的方程为+=1,即4x+3y=12, 可设P(m,n),(0≤n≤4),即有m=3﹣n, 则=|(﹣3﹣m,﹣n)+(3﹣m,﹣n)|=|(﹣2m,﹣2n)|=2 =2=2, 当n=∈[0,4],可得的最小值为2×=; 当n=4时,可得的最大值为8, 则的取值范围是[,8]. 故选:D. 二、填空题共5小题,每小题5分,共25分. 11.设复数z=1+i,则z的模|z|= . 【分析】直接代入模长公式即可. 解:因为复数z=1+i,则z的模|z|==; 故答案为:. 12.数据19,20,21,23,25,26,27,则这组数据的方差是 . 【分析】根据题意,先求出这组数据的平均数,进而由方差计算公式计算可得答案. 解:根据题意,数据19,20,21,23,25,26,27,其平均数=(19+20+21+23+25+26+27)=23, 则其方差S2=[(19﹣23)2+(20﹣23)2+(21﹣23)2+(23﹣23)2+(25﹣23)2+(26﹣23)2+(27﹣23)2]=; 故答案为:. 13.三棱锥的三条侧棱两两垂直,长分别为1,2,3,则这个三棱锥的体积为 1 . 【分析】由已知画出图形,再由等体积法求三棱锥的体积. 解:如图,三棱锥P﹣ABC的三条侧棱两两垂直, 不妨设PA=1,PB=2,PC=3. 则, 由PC⊥PA,PC⊥PB,PA∩PB=P,得PC⊥平面PAB. ∴VP﹣ABC=VC﹣PAB=. 故答案为:1. 14.已知=(1,2),=(2,y),|+|=|﹣|,则y= ﹣1 . 【分析】可以求出,然后根据即可得出9+(y+2)2=1+(2﹣y)2,解出y即可. 解:,, ∵, ∴9+(y+2)2=1+(2﹣y)2,解得y=﹣1. 故答案为:﹣1. 15.在△ABC中,b=10,A=. ①若a=5,则角B大小为 ; ②若角B有两个解,则a的取值范围是 (5,10) . 【分析】①根据正弦定理带入计算即可; ②由正弦定理表示出sinB,根据B的度数确定出B的范围,要使三角形有两解确定出B的具体范围,利用正弦函数的值域求出x的范围即可. 解:①由正弦定理可得sinB===1,故B=; ②∵在△ABC中,b=10,A=, ∴由正弦定理得:sinB==, ∵A=30°, ∴0<B<150°, 要使三角形有两解,得到30°<B<150°,且B≠90°,即<sinB<1, ∴<<1, 解得:5<a<10,即:a∈(5,10). 故答案为:;(5,10). 三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。 16.已知复数z=(m2﹣m)+(m+3)i(m∈R)在复平面内对应点Z. (Ⅰ)若m=2,求z; (Ⅱ)若点Z在直线y=x上,求m的值. 【分析】(Ⅰ)由m求得z,再由求解; (Ⅱ)由题意,可得z的实部与虚部相等,由此可得关于m的方程求解. 解:(Ⅰ)∵m=2,∴z=2+5i, 则; (Ⅱ)若点Z在直线y=x上,则m2﹣m=m+3, 即m2﹣2m﹣3=0,解得m=﹣1或m=3. 17.已知三个点A(2,1),B(3,2),D(﹣1,4). (Ⅰ)求证:AB⊥AD; (Ⅱ)若四边形ABCD为矩形,求点C的坐标及矩形ABCD两对角线所成锐角的余弦值. 【分析】(Ⅰ)求出向量的坐标,利用向量的数量积为0,两向量垂直证出两线垂直. (Ⅱ)利用向量相等对应的坐标相等求出点C的坐标,求出两对角线对应的向量坐标,利用向量的数量积公式求出向量的夹角. 【解答】(Ⅰ)证明:可得,,, ∴AB⊥AD; (Ⅱ)由(Ⅰ)及四边形ABCD为矩形,得,设C(x,y), 则(1,1)=(x+1,y﹣4),∴,得,即C(0,5); ∴, 得,, 设与夹角为θ,则, ∴该矩形对角线所夹的锐角的余弦值. 18.为了解某小区7月用电量情况,通过抽样,获得了100户居民7月用电量(单位:度),将数据按照[50,100),[100,150),…,[300,350]分成六组,制成了如图所示的频率分布直方图. (Ⅰ)求频率分布直方图中x的值; (Ⅱ)已知该小区有1000户居民,估计该小区7月用电量不低于200度的户数,并说明理由; (Ⅲ)估计该小区85%的居民7月用电量的值,并说明理由. 【分析】(Ⅰ)由概率统计相关知识,各组频率和为1,列出方程求出x的值; (Ⅱ)由频率分布直方图可得100户居民7月用电量不低于200度的频率为(0.0044+0.0024+0.0012)×50=0.4,由此得解. (Ⅲ)由频率分布直方图可得85%分位数一定位于区间(250.300)内,由此得解. 解:(Ⅰ)由频率分布直方图可得:(0.0024+0.0036+0.0060+x+0.0024+0.0012)×50=1, 解得:x=0.0044. (Ⅱ)由频率分布直方图可得,100户居民7月用电量不低于200度的频率为(0.0044+0.0024+0.0012)×50=0.4, 由此可以估计该小区有1000户居民7月用电量不低于200度的户数为1000×0.4=400. (Ⅲ)由频率分布直方图可得,7月用电量低于250度的频率为0.82,7月用电量低于300度的频率为0.94, 所以85%分位数一定位于区间(250.300)内, 由250+50×=262.5. 由此估计该小区85%的居民7月用电量约为262.5度. 19.如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC. (Ⅰ)求BD的长; (Ⅱ)求sin∠BDC的值. 【分析】(I)由已知可求AC,cosA,然后结合余弦定理可求BD, (II)由已知结合正弦定理即可求解. 解:(I)因为∠ABC=90°,AB=4,BC=3, 所以AC=5,cosA=, 又点D在线段AC上,且AD=4DC, 所以AD=4,△ABD 中,由余弦定理可得,BD2=AB2+AD2﹣2AB•AD•cosA, ==, 所以BD=; (II)因为sinC=cosA=, △BCD中,由正弦定理可得,, 所以sin∠BDC== 20.如图所示,在正方体ABCD﹣A1B1C1D1中,AA1=1. (Ⅰ)求证:BD⊥A1C; (Ⅱ)求证:平面BDC1⊥平面A1B1C; (Ⅲ)用一张正方形的纸把正方体ABCD﹣A1B1C1D1完全包住,不将纸撕开,求所需纸的最小面积.(结果不要求证明) 【分析】(Ⅰ)连结AC,推导出AC⊥BD,BD⊥AA1,从而BD⊥平面A1AC,由此能证明BD⊥A1C. (Ⅱ)推导出BC1⊥B1C,A1B1⊥BC1,由此能证明BC1⊥平面A1B1C,从而平面BDC1⊥平面A1B1C; (Ⅲ)所需纸的最小面积为8. 解:(Ⅰ)证明:连结AC,在正方体ABCD﹣A1B1C1D1中, ∵底面ABCD是正方形,∴AC⊥BD, ∵AA1⊥平面ABCD,∴BD⊥AA1, ∵AA1∩AC=A,∴BD⊥平面A1AC, ∵A1C⊂平面A1AC,∴BD⊥A1C. (Ⅱ)证明:∵侧面BCC1B1是正方形,∴BC1⊥B1C, ∵A1B1⊥平面BCC1B1,∴A1B1⊥BC1, ∵A1B1∩B1C=B1,∴BC1⊥平面A1B1C, ∵BC1⊂平面BDC1,∴平面BDC1⊥平面A1B1C; (Ⅲ)用一张正方形的纸把正方体ABCD﹣A1B1C1D1完全包住, 不将纸撕开,所需纸的最小面积为8. 21.如图所示,在四棱锥P﹣ABCD中,BC∥平面PAD,BC=AD,E是PD的中点. (Ⅰ)求证:BC∥AD; (Ⅱ)求证:CE∥平面PAB; (Ⅲ)若M是线段CE上一动点,则线段AD上是否存在点N,使MN∥平面PAB?说明理由. 【分析】(Ⅰ)根据线面平行的性质定理即可证明; (Ⅱ)取PA的中点F,连接EF,BF,利用中位线的性质,平行四边形的性质,以及线面平行的判断定理即可证明; (Ⅲ)取AD中点N,连接CN,EN,根据线面平行的性质定理和判断定理即可证明. 【解答】证明:(Ⅰ)在四棱锥P﹣ABCD中,BC∥平面PAD,BC⊂平面ABCD, 平面ABCD∩平面PAD=AD, ∴BC∥AD, (Ⅱ)取PA的中点F,连接EF,BF, ∵E是PD的中点, ∴EF∥AD,EF=AD, 又由(Ⅰ)可得BC∥AD,BC=AD, ∴BC∥EF,BC=EF, ∴四边形BCEF是平行四边形, ∴CE∥BF, ∵CE⊄平面PAB,BF⊂平面PAB, ∴CE∥平面PAB. (Ⅲ)取AD中点N,连接CN,EN, ∵E,N分别为PD,AD的中点, ∴EN∥PA, ∵EN⊄平面PAB,PA⊂平面PAB, ∴EN∥平面PAB, 又由(Ⅱ)可得CE∥平面PAB,CE∩EN=E, ∴平面CEN∥平面PAB, ∵M是CE上的动点,AN⊂平面CEN, ∴MN∥平面PAB, ∴线段AD存在点N,使得MN∥平面PAB.查看更多