高中数学必修1公开课教案1_2_2 函数的表示法 第2课时

高中数学必修1公开课教案1_2_2 函数的表示法 第2课时

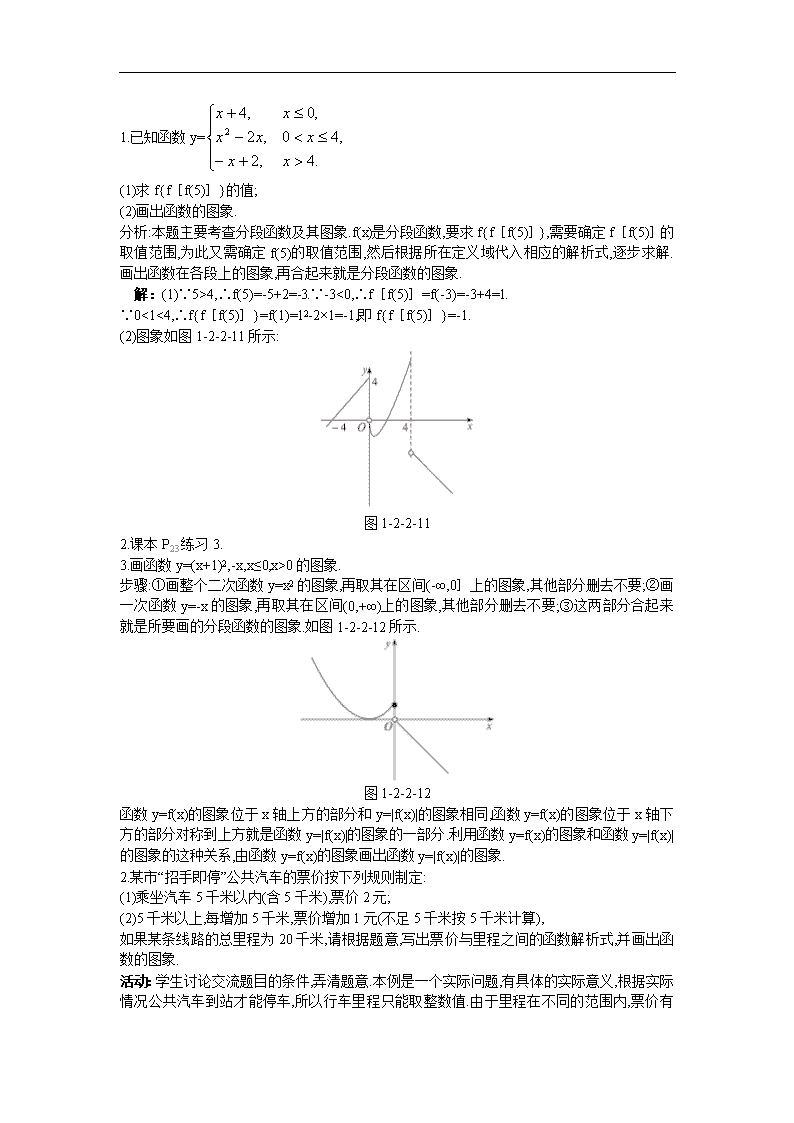
第2课时 分段函数 导入新课 思路1.当x>1时,f(x)=x+1;当x≤1时,f(x)=-x,请写出函数f(x)的解析式.这个函数的解析式有什么特点？教师指出本节课题.‎ 思路2.化简函数y=|x|的解析式,说说此函数解析式的特点,教师指出本节课题.‎ 推进新课 新知探究 提出问题 ‎①函数h(x)=与f(x)=x-1,g(x)=x2在解析式上有什么区别?‎ ‎②请举出几个分段函数的例子.‎ 活动：学生讨论交流函数解析式的区别.所谓“分段函数”,习惯上指在定义域的不同部分,有不同对应法则的函数.并让学生结合体会来实际举例.‎ 讨论结果：①函数h(x)是分段函数,在定义域的不同部分,其解析式不同.说明:分段函数是一个函数,不要把它误认为是几个函数;分段函数的定义域是各段定义域的并集,值域是各段值域的并集;生活中有很多可以用分段函数描述的实际问题,如出租车的计费、个人所得税纳税额等等.‎ ‎②例如:y=等.‎ 应用示例 思路1‎ ‎1.画出函数y=|x|的图象.‎ 活动：学生思考函数图象的画法:①化简函数的解析式为基本初等函数;②利用变换法画出图象,根据绝对值的概念来化简解析式.‎ 解法一：由绝对值的概念,我们有y=‎ 所以,函数y=|x|的图象如图1-2-2-10所示.‎ 图1-2-2-10‎ 解法二：画函数y=x的图象,将其位于x轴下方的部分对称到x轴上方,与函数y=x的图象位于x轴上方的部分合起来得函数y=|x|的图象如图1-2-2-10所示.‎ 变式训练 ‎1.已知函数y=‎ ‎(1)求f{f［f(5)］}的值;‎ ‎(2)画出函数的图象.‎ 分析:本题主要考查分段函数及其图象.f(x)是分段函数,要求f{f［f(5)］},需要确定f［f(5)］的取值范围,为此又需确定f(5)的取值范围,然后根据所在定义域代入相应的解析式,逐步求解.画出函数在各段上的图象,再合起来就是分段函数的图象.‎ ‎ 解：(1)∵5>4,∴f(5)=-5+2=-3.∵-3<0,∴f［f(5)］=f(-3)=-3+4=1.‎ ‎∵0<1<4,∴f{f［f(5)］}=f(1)=12-2×1=-1,即f{f［f(5)］}=-1.‎ ‎(2)图象如图1-2-2-11所示:‎ 图1-2-2-11‎ ‎2.课本P23练习3.‎ ‎3.画函数y=(x+1)2,-x,x≤0,x>0的图象.‎ 步骤:①画整个二次函数y=x2的图象,再取其在区间(-∞,0］上的图象,其他部分删去不要;②画一次函数y=-x的图象,再取其在区间(0,+∞)上的图象,其他部分删去不要;③这两部分合起来就是所要画的分段函数的图象.如图1-2-2-12所示.‎ 图1-2-2-12‎ 函数y=f(x)的图象位于x轴上方的部分和y=|f(x)|的图象相同,函数y=f(x)的图象位于x轴下方的部分对称到上方就是函数y=|f(x)|的图象的一部分.利用函数y=f(x)的图象和函数y=|f(x)|的图象的这种关系,由函数y=f(x)的图象画出函数y=|f(x)|的图象.‎ ‎2.某市“招手即停”公共汽车的票价按下列规则制定:‎ ‎(1)乘坐汽车5千米以内(含5千米),票价2元;‎ ‎(2)5千米以上,每增加5千米,票价增加1元(不足5千米按5千米计算),‎ 如果某条线路的总里程为20千米,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.‎ 活动：学生讨论交流题目的条件,弄清题意.本例是一个实际问题,有具体的实际意义,根据实际情况公共汽车到站才能停车,所以行车里程只能取整数值.由于里程在不同的范围内,‎ 票价有不同的计算方法,故此函数是分段函数.‎ 解：设里程为x千米时,票价为y元,根据题意得x∈(0,20］.‎ 由空调汽车票价制定的规定,可得到以下函数解析式:‎ 图1-2-2-13‎ y=‎ 根据这个函数解析式,可画出函数图象,如图1-2-2-13所示.‎ 点评：本题主要考查分段函数的实际应用,以及应用函数解决问题的能力.生活中有很多可以用分段函数描述的实际问题,如出租车的计费、个人所得税纳税额等等.在列出其解析式时,要充分考虑实际问题的规定,根据规定来求得解析式.‎ 注意：①本例具有实际背景,所以解题时应考虑其实际意义;‎ ‎②分段函数的解析式不能写成几个不同的方程,而应写成函数值几种不同的表达式并用一个左大括号括起来,并分别注明各部分的自变量的取值情况.‎ 变式训练2007上海中学高三测试,理7某客运公司确定客票价格的方法是:如果行程不超过100千米,票价是每千米0.5元,如果超过100千米,超过部分按每千米0.4元定价,则客运票价y(元)与行程千米数x(千米)之间的函数关系式是________.‎ 分析:根据行程是否大于100千米来求出解析式.‎ 答案：y=‎ 思路2‎ ‎1.已知函数f(x)=‎ ‎(1)求f(-1),f［f(-1)］,f{f［f(-1)］}的值;‎ ‎(2)画出函数的图象.‎ 活动：此函数是分段函数,应注意在不同的自变量取值范围内有不同的对应关系.‎ 解：(1)f(-1)=0;f[f(-1)]=f(0)=1;f{f[f(-1)]}=f(1)=-12+2×1=1.‎ ‎(2)函数图象如图1-2-2-14所示:‎ 图1-2-2-14‎ 变式训练 ‎2007福建厦门调研,文10若定义运算a⊙b=则函数f(x)=x⊙(2-x)的值域是________.‎ 分析:由题意得f(x)=画函数f(x)的图象得值域是(-∞,1］.‎ 答案：(-∞,1］‎ 点评：本题主要考查分段函数的解析式和图象.求分段函数的函数值时,要注意自变量在其定义域的哪一段上,依次代入分段函数的解析式.画分段函数y=(D1,D2,…,两两交集是空集)的图象步骤是 ‎(1)画整个函数y=f1(x)的图象,再取其在区间D1上的图象,其他部分删去不要;‎ ‎(2)画整个函数y=f2(x)的图象,再取其在区间D2上的图象,其他部分删去不要;‎ ‎(3)依次画下去;‎ ‎(4)将各个部分合起来就是所要画的分段函数的图象.‎ ‎2.如图1-2-2-15所示,在梯形ABCD中,AB=10,CD=6,AD=BC=4,动点P从B点开始沿着折线BC、CD、DA前进至A,若P点运动的路程为x,△PAB的面积为y.‎ 图1-2-2-15‎ ‎(1)写出y=f(x)的解析式,指出函数的定义域;‎ ‎(2)画出函数的图象并求出函数的值域.‎ 活动：学生之间相互讨论交流,教师帮助学生审题读懂题意.首先通过画草图可以发现,P点运动到不同的位置,y的求法是不同的(如图1-2-2-16的阴影部分所示).‎ 图1-2-2-16‎ 可以看出上述三个阴影三角形的底是相同的,它们的面积由其高来定,所以只要由运动里程x来求出各段的高即可.三角形的面积公式为底乘高除以2,则△PAB的面积的计算方式由点P 所在的位置来确定.‎ 解：(1)分类讨论:‎ ‎①当P在BC上运动时,易知∠B=60°,则知 y=×10×(xsin60°)=x,0≤x≤4.‎ ‎②当P点在CD上运动时,‎ y=×10×2=10,40,x=0,x<0段上的图象,合在一起得函数的图象.‎ ‎(1)如图1-2-2-19所示,画法略.‎ 图1-2-2-19‎ ‎(2)f(1)=12=1,f(-1)==1,f［f(-1)］=f(1)=1.‎ ‎3.某人驱车以52千米/时的速度从A地驶往260千米远处的B地,到达B地并停留1.5小时后,再以65千米/时的速度返回A地.试将此人驱车走过的路程s(千米)表示为时间t的函数.‎ 分析:本题中的函数是分段函数,要由时间t属于哪个时间段,得到相应的解析式.‎ 解：从A地到B地,路上的时间为=5(小时);从B地回到A地,路上的时间为=4(小时).所以走过的路程s(千米)与时间t的函数关系式为 s=‎ 拓展提升 问题:已知函数y=1,f(n+1)=f(n)+2,n=1,n∈N*.‎ ‎(1)求:f(2),f(3),f(4),f(5);‎ ‎(2)猜想f(n),n∈N*.‎ 探究:(1)由题意得f(1)=1,则有 f(2)=f(1)+2=1+2=3,‎ f(3)=f(2)+2=3+2=5,‎ f(4)=f(3)+2=5+2=7,‎ f(5)=f(4)+2=7+2=9.‎ ‎(2)由(1)得 f(1)=1=2×1-1,‎ f(2)=3=2×2-1,‎ f(3)=5=2×3-1,‎ f(4)=7=2×4-1,‎ f(5)=9=2×5-1.‎ 因此猜想f(n)=2n-1,n∈N*.‎ 课堂小结 本节课学习了:画分段函数的图象;求分段函数的解析式以及分段函数的实际应用.‎ 作业 课本P25习题1.2 B组 3、4.‎ 设计感想 本节教学设计容量较大,特别是例题条件有图,建议使用信息技术来完成.本节重点设计了分段函数,这是课标明确要求也是高考的重点,通过分段函数问题能够区分学生的思维层次,因此教学中应予以重视.‎ ‎(设计者：刘菲)‎