- 2021-04-17 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学冀教版九年级上册教案28-4垂径定理
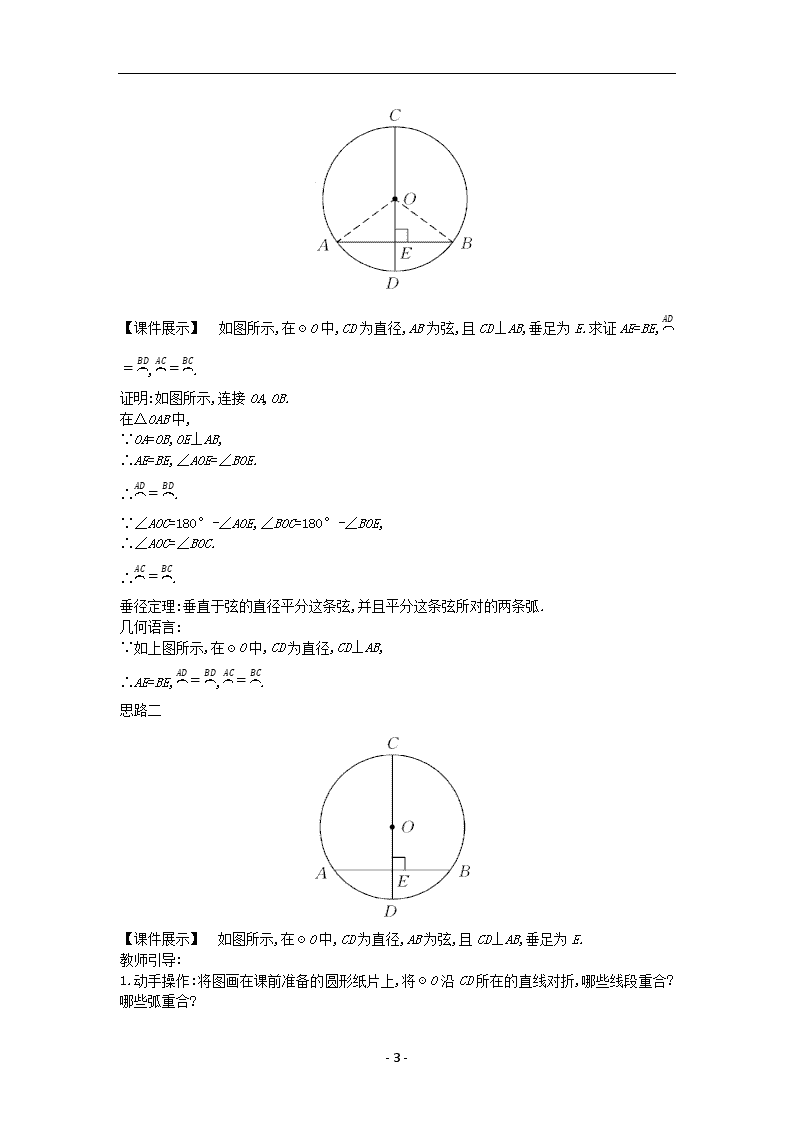
- 1 - 28.4 垂径定理 教学目标 【知识与能力】 .理解垂径定理的证明过程,掌握垂径定理及其推论. 2.会用垂径定理进行简单的证明和计算. 3.了解直径、弦、弧之间的特殊关系. 【过程与方法】 1.通过探索垂径定理的过程,培养学生动手实践、观察分析、逻辑思维和归纳概括的能力. 2.让学生经历“实验——观察——猜想——验证——归纳”的探究过程,培养学生发现问题、 分析问题、解决问题的能力. 3.通过本节课的学习,发展学生的数学思维,让学生体验数学来源于生活又应用于生活. 【情感态度价值观】 1.通过探究垂径定理的活动,激发学生探究、发现数学问题的兴趣,培养学生大胆猜想、乐于 探究的良好品质. 2.培养学生观察能力,激发学生的好奇心和求知欲,并从数学学习活动中获得成功的体验. 3.经历将已学知识应用到未学知识的探索过程,激发学生探究、发现数学问题的兴趣和欲望. 教学重难点 【教学重点】 垂径定理及其应用. 【教学难点】 探索并证明垂径定理及利用垂径定理解决一些实际问题. 课前准备 多媒体课件 教学过程 一、新课导入: 导入一: [导入语] 这座桥是我国隋代工匠李春建造的赵州桥(如图所示).因它位于现在的历史文化 名城河北省赵县(古称赵州)而得名,是世界上现存最早、保存最好的巨大石拱桥,被誉为“华 北四宝之一”,它的结构是当时世界桥梁界的首创,这充分显示了我国古代劳动人民的创造智 慧. 【课件展示】 赵州桥是我国隋代建造的石拱桥,距今约有 1400 年的历史,是我国古代人民 勤劳和智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37.4 m,拱高(弧的 中点到弦的距离)为 7.2 m,你能求出赵州桥主桥拱的半径吗?(结果保留小数点后一位) [过渡语] 要解决这个实际问题,我们的知识储备还不够,通过这节课的学习,我们将能 - 2 - 解决这类和圆有关的实际问题. 导入二: 复习提问: 1.什么是轴对称图形? 2.圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴? 3.你是用什么方法解决上述问题的? (教师引导折叠课前准备的圆形纸片) 4.直径是圆的对称轴正确吗? 【师生活动】 学生思考后回答,教师点评,指出“直径是圆的对称轴”这个结论的错误原因. 师生共同归纳:圆是轴对称图形,其对称轴是任意一条过圆心的直线(或直径所在的直线). [设计意图] 通过生活实际问题导入新课,让学生感受数学来源于生活,又应用于生活.通过 复习旧知识和创设动手操作活动,激发学生学习兴趣,探索圆的对称性,引出本节内容,为本 节课的学习做好铺垫. 二、新知构建: [过渡语] 我们知道了圆是轴对称图形,利用圆的轴对称性,我们还可以发现圆的一些 性质. 一、垂径定理 思路一 教师引导操作、思考、回答: 在自己课前准备的纸片上作图: 1.任意作一条弦 AB. 2.过圆心 O 作弦 AB 的垂线,得直径 CD 交 AB 于点 E. 3.观察图形,你能找到哪些线段相等?哪些弧相等? 4.沿着 CD 所在的直线折叠,观察有哪些相等的线段、弧. 5.图形中的已知是什么?你得到的结论是什么?你能写出你的证明过程吗? 6.你能用语言叙述这个命题吗? 7.你得到的结论怎样用几何语言表示? 【师生活动】 学生在教师的引导下操作、观察、思考、尝试证明,然后小组合作交流,共同 探究结论.教师在巡视过程中,帮助有困难的学生.学生回答问题,并展示自己的证明过程,教 师适时点评,规范学生的证明过程,师生共同回忆操作过程,归纳结论. - 3 - 【课件展示】 如图所示,在☉O 中,CD 为直径,AB 为弦,且 CD⊥AB,垂足为 E.求证 AE=BE, 晦 = 晦 , = . 证明:如图所示,连接 OA,OB. 在△OAB 中, ∵OA=OB,OE⊥AB, ∴AE=BE,∠AOE=∠BOE. ∴ 晦 = 晦 . ∵∠AOC=180°-∠AOE,∠BOC=180°-∠BOE, ∴∠AOC=∠BOC. ∴ = . 垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧. 几何语言: ∵如上图所示,在☉O 中,CD 为直径,CD⊥AB, ∴AE=BE, 晦 = 晦 , = . 思路二 【课件展示】 如图所示,在☉O 中,CD 为直径,AB 为弦,且 CD⊥AB,垂足为 E. 教师引导: 1.动手操作:将图画在课前准备的圆形纸片上,将☉O 沿 CD 所在的直线对折,哪些线段重合? 哪些弧重合? - 4 - (AE 与 BE, 晦 与 晦 , 与 ) 2.由此你能得出什么结论?尝试说出你的猜想. (通过探究,我们发现:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧) 3.你能证明你得到的结论吗? 【师生活动】 学生在教师的引导下完成画图、折叠、观察、归纳、猜想,学生独立思考证 明思路后,小组合作交流,小组代表板书证明过程,教师点评,规范书写格式,师生共同回忆归 纳结论. 【课件展示】 如图所示,在☉O 中,CD 为直径,AB 为弦,且 CD⊥AB,垂足为 E.求证 AE=BE, 晦 = 晦 , = . 证明过程同思路一. 垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧. 几何语言: ∵如上图所示,在☉O 中,CD 为直径,CD⊥AB, ∴AE=BE, 晦 = 晦 , = . [设计意图] 通过学生动手操作、观察、分析、交流,教师引导归纳出垂直于弦的直径的性 质,经历知识的形成过程,培养学生观察能力和归纳概括能力,提高分析问题、解决问题的能 力,同时感受圆的对称美. 二、垂径定理的推论 【课件展示】 如图所示,在☉O 中,直径 CD 与弦 AB(非直径)相交于点 E. 【思考】 - 5 - (1)若 AE=BE,能判断 CD 与 AB 垂直吗? 晦 与 晦 (或 与 )相等吗?说明你的理由. (2)若 晦 = 晦 (或 = ),能判断 CD 与 AB 垂直吗?AE 与 BE 相等吗?说明你的理由. 【师生活动】 学生独立思考,小组合作交流,独立书写解答过程,小组代表展示,教师对学生 的展示点评,规范书写格式. 解:(1)CD⊥AB, 晦 = 晦 (或 = ). 理由是:连接 OA,OB,如图所示,则△OAB 是等腰三角形, ∵AE=BE,∴CD⊥AB. 由垂径定理可得 晦 = 晦 , = . (2)CD⊥AB,AE=BE. 理由是:连接 OA,OB,如图所示, ∵ 晦 = 晦 ,∴∠AOD=∠BOD, 又∵OA=OB,OE=OE,∴△AEO≌△BEO, ∴∠AEO=∠BEO,AE=BE, ∴CD⊥AB. 追加思考: (1)垂径定理中的条件和结论分别是什么?用语言叙述. (2)上面思考(1)(2)中的条件和结论分别是什么? (3)如果不要求“弦不是直径”上述结论还成立吗? 【师生活动】 师生共同分析解答,通过追加思考,师生共同归纳结论. - 6 - 【课件展示】 在☉O 中,设直径 CD 与弦 AB(非直径)相交于点 E.若把 AE=BE,CD⊥AB, 晦 = 晦 中的一项作为条件,则可得到另外两项结论. [设计意图] 通过教师提出的问题,学生合作交流,共同分析解答,提高学生合作意识,加深 对垂径定理的理解和记忆,通过追加思考,师生共同分析得出垂径定理中五个条件:过圆心、 垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧中,以其中两个为条件,可以得到 其他三个结论. 三、例题讲解 [过渡语] 我们学习了垂径定理及推论,就可以解决一些圆中的计算问题. 【课件展示】 (教材 164 页例)如图所示,已知 CD 为☉O 的直径,AB 为弦,且 AB⊥CD,垂足为 E.若 ED=2,AB=8,求直径 CD 的长. 教师引导思考: 1.如何把圆的半径转化为三角形中的线段? (连接半径,构造直角三角形) 2.构造的直角三角形中三边之间有什么特点? (根据垂径定理得三角形一边是弦长的一半,另两边的长正好相差 ED 长) 3.直角三角形中已知一边、另外两边之间的关系,如何求另两边长? (设未知数,用勾股定理列方程求解) 【师生活动】 教师引导,师生共同完成思考分析,学生小组合作交流解题思路,书写解题过 程,小组代表板书,教师点评,规范解答格式. 【课件展示】 解:如图所示,连接 OA. 设☉O 的半径为 r. - 7 - ∵CD 为☉O 的直径,AB⊥CD, ∴AE=BE. ∵AB=8, ∴AE=BE=4. 在 Rt△OAE 中, OA2=OE2+AE2,OE=OD-ED, 即 r2=(r-2)2+42. 解得 r=5,从而 2r=10. 所以直径 CD 的长为 10. [设计意图] 以问题的形式,教师引导,师生共同分析解决,降低了例题的难度,体会方程思 想在数学中的应用,同时掌握一类题型的解题方法,应用垂径定理计算时,常作辅助线构造直 角三角形,体会数形结合思想在解题中的应用,提高学生分析问题的能力. [过渡语] 经过这节课的学习,让我们看看能不能解决课前导入中的实际问题吧. 【课件展示】 (课前导入一)赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代 人民勤劳和智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37.4 m,拱高 (弧的中点到弦的距离)为 7.2 m,你能求出赵州桥主桥拱的半径吗?(结果保留小数点后一位) 【师生活动】 教师引导学生画出对应的几何图形,根据所画图形,学生独立完成解答过程, 小组合作交流答案,教师在巡视过程中帮助有困难的学生,教师展示课件,规范解答格式. 【课件展示】 解:如图所示,用 表示主桥拱,设 所在圆的圆心为 O,半径为 R. 经过圆心 O 作弦 AB 的垂线 OC,D 为垂足,OC 与 相交于点 C,连接 OA.根据垂径定理知 D 为 AB 的中点,C 为 的中点,CD 就是拱高. 由题设可知,AB=37.4 m,CD=7.2 m, 所以 AD= 1 2 AB= 1 2 ×37.4=18.7(m), OD=OC-CD=R-7.2(m). 在 Rt△OAD 中,由勾股定理,得 OA2=AD2+OD2, 即 R2=18.72+(R-7.2)2.解得 R≈27.9(m). 因此,赵州桥的主桥拱半径约为 27.9 m. 【思考】 1.在圆中解决有关弦的问题,常作什么辅助线? - 8 - 2.在圆中解决有关弦的问题,常用什么方法? 【师生活动】 学生思考回答后,教师归纳总结. 在圆中解决有关弦的问题时,常常过圆心作弦的垂线段(弦心距),通过作辅助线,把垂径定理 和勾股定理结合,得到圆的半径 r、弦心距 d、弦长 a 的一半之间的关系式:r2=d2+ 2 2 . [设计意图] 教师引导学生在实际问题中画出符合题意的几何图形,建立数学模型,根据垂 径定理和勾股定理列方程求解所在圆的半径,让学生体会数学来源于生活,又应用于生活中, 提高学生分析问题、解决问题的能力,同时在整个教学设计中达到首尾呼应,增强学生应用意 识. [知识拓展] 1.由垂径定理可以得到以下结论: (1)若直径垂直于弦,则直径平分弦及其所对的两条弧. (2)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. (3)垂直且平分一条弦的弦是直径. (4)连接弦所对的两条弧的中点的线段是直径. 综上所述,可以知道在①过圆心,②垂直于弦,③平分弦,④平分弦所对的劣弧,⑤平分弦所对 的优弧这五项中满足其中任意两项,就可以推出另外三项,简称“5.2.3”定理. 2.利用垂径定理及其推论可以证明平分弧、平分弦,证明垂直,证明一条线段是直径. 3.利用垂径定理的推论可以确定圆心的位置:在圆中找两条不平行的弦,分别作两条弦的垂 直平分线,两条垂直平分线的交点即是圆心. 4.由于垂直于弦的直径平分弦,因此可以在圆中构造直角三角形,利用勾股定理列方程求弦 长(或半径). 5.圆心到弦的距离叫做弦心距. 三、课堂小结: 1.垂径定理和推论及它们的应用. 2.垂径定理和勾股定理相结合,将圆的问题转化为直角三角形问题. 3.圆中常作辅助线连半径、过圆心作弦的垂线.查看更多