2019九年级数学上册 第1章 1用一元二次方程解决问题

2019九年级数学上册 第1章 1用一元二次方程解决问题

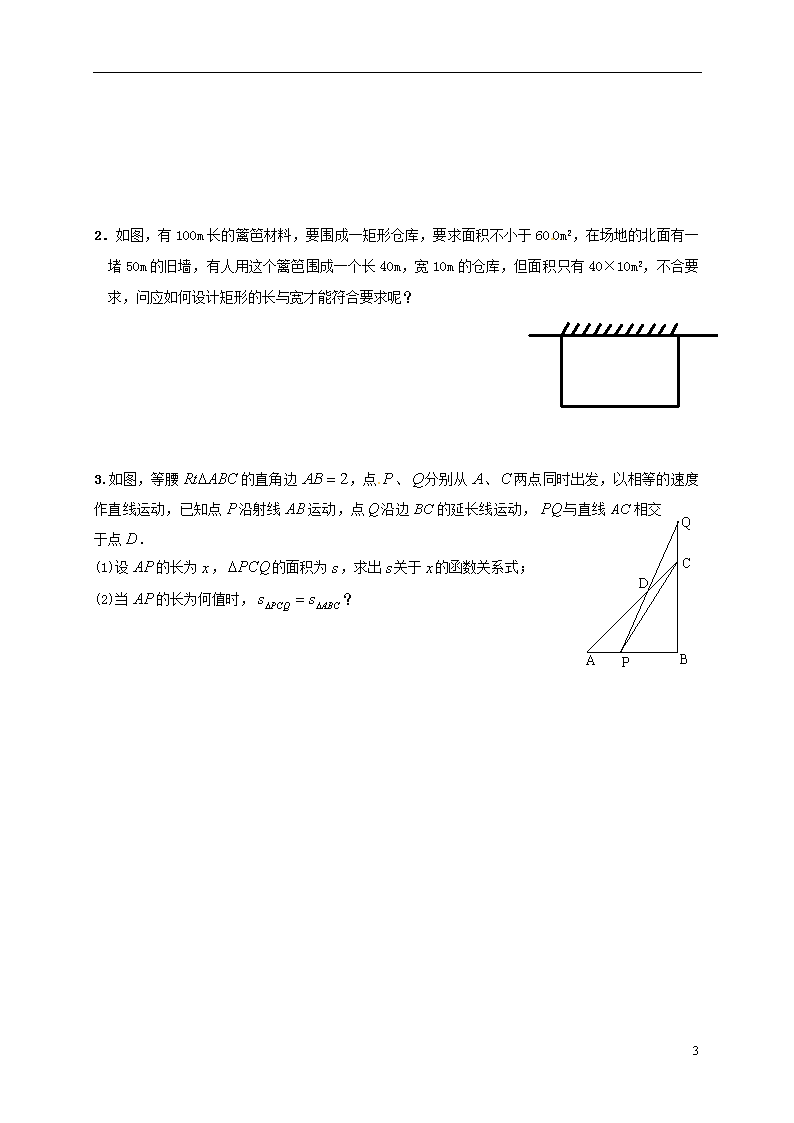
课题: 1.4　用一元二次方程解决问题（3）‎ 学习目标： ‎ 1. 经历和体验用一元二次方程解决实际问题的过程，进一步体会一元二次方程是刻画现实世界数量关系的有效模型；‎ 2. 会根据具体问题中的数量关系列出一元二次方程并求解，培养学生的数学应用能力；‎ 3. 能检验所得的问题结果是否符合实际意义，进一步提高学生逻辑思维能力、分析和解决问题的能力． ‎ 学习重点：分析和解决问题．‎ 学习难点：根据具体问题中的数量关系列出一元二次方程．‎ 学习过程 ： ‎ 一.【情境创设】‎ 在矩形中，，.点沿边从点开始向点以的速度移动，点沿边从点开始向点以的速度移动.如果、同时出发，用表示移动的时间.那么当为何值时，的面积等于？‎ 二.【问题探究】‎ 问题5： 如图，某海关缉私艇在C处发现在正北方向‎30km的A处有一艘可疑船只，并测得它正以‎60km/h的速度向正东方向航行．缉私艇随即以‎75km/h的速度前往拦截，在B处将可疑船只拦截．缉私艇从C处到B处需航行多长时间？‎ B A C 北 3‎ 问题6：如图，在矩形ABCD中，AB＝‎6cm，BC＝‎12cm，点P从点A出发沿AB以‎1cm/s的速度向点B移动；同时，点Q从点B出发沿BC以‎2cm/s的速度向点CA B C D P Q 移动．几秒钟后△DPQ的面积等于‎28cm2？‎ 三.【拓展提升】 ‎ 问题7.如图，有长为米的篱笆，一面利用墙（墙的最大可用长度为为米），围成中间隔有一道篱笆的长方形花圃.‎ ‎（1）如果要围成面积为平方米的花圃，的长是多少米？‎ ‎（2）能围成面积比平方米更大的花圃吗？‎ 如果能，请求出最大面积，并说明围法；如果不能，请说明理由.‎ 四.【课堂小结】 ‎ ‎ 如何从实际情境中抽象出方程的模式？‎ 五.【反馈练习】‎ 姓名 班级 ‎ ‎1.如图，在中，，点从点开始沿边以的速度向点移动，移动过程中始终保持∥，∥，问点出发几秒后四边形面积为？‎ 3‎ ‎2．如图，有‎100m长的篱笆材料，要围成一矩形仓库，要求面积不小于60‎0m2‎，在场地的北面有一堵‎50m的旧墙，有人用这个篱笆围成一个长‎40m，宽‎10m的仓库，但面积只有40×‎10m2‎，不合要求，问应如何设计矩形的长与宽才能符合要求呢？‎ C D P Q B A ‎3.如图，等腰的直角边，点、分别从、两点同时出发，以相等的速度作直线运动，已知点沿射线运动，点沿边的延长线运动，与直线相交于点.‎ ‎(1)设的长为，的面积为，求出关于的函数关系式； ‎ ‎(2)当的长为何值时，？‎ ‎ ‎ 3‎