- 2021-04-16 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2015徐汇区初三一模数学
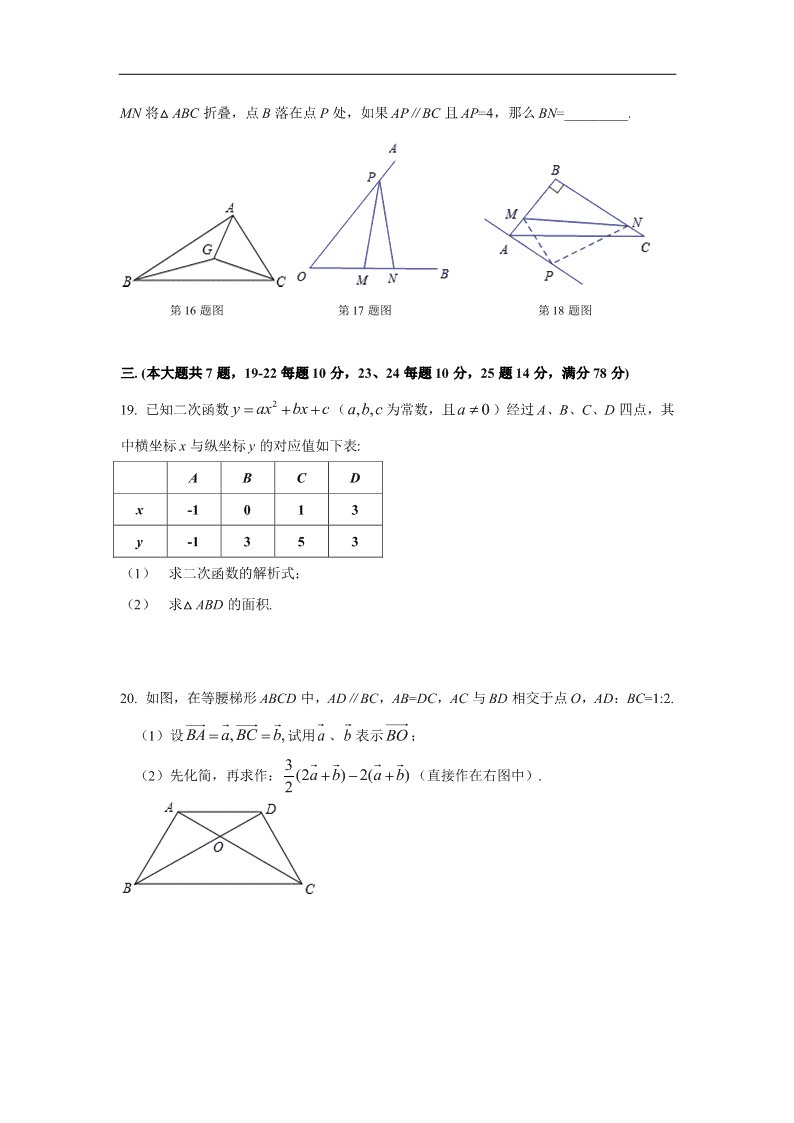
2014 学年第一学期徐汇区学习能力诊断卷 初三数学 试卷 (时间 100 分钟 满分 150 分) 一. 选择题(本大题共 6 题,每题 4 分,满分 24 分) 1. 将抛物线 22yx 向右平移 1 个单位,再向上平移 2 个单位后,抛物线的表达式为( ) A. 22( 1) 2;yx B. 22( 1) 2;yx C. 22( 1) 2;yx D. 22( 1) 2;yx 2. 如图,□ABCD 中,E 是边 BC 上的点,AE 交 BD 于点 F,如果 BE:BC=2:3,那么下列 各式错误的是( ) A. 2;BE EC B. 1;3 EC AD C. 2;3 EF AE D. 2;3 BF DF 第 2 题图 第 4 题图 第 6 题图 3. 已知 Rt△ ABC 中,∠C=90°,∠CAB= ,AC=7,那么 BC 为( ) A. 7sin ; B. 7cos ; C. 7 tan ; D. 7cot . 4. 如图,在四边形 ABCD 中,AD∥BC,如果添加下列条件,不能使得△ ABC∽△DCA 成 立的是( ) A. ∠BAC=∠ADC; B. ∠B=∠ACD; C. 2 ;AC AD BC D. .DC AB AC BC 5. 已知二次函数 2 2 2( 0)y ax x a ,那么它的图像一定不经过( ) A. 第一象限; B. 第二象限; C. 第三象限 ; D. 第四象限. 6. 如图,在△ ABC 中,D、E 分别是 AB、AC 上的点,且 DE∥BC,如果 AE:EC=1:4,那 么 S△ ADE:S△ BEC=( ) A. 1:24; B. 1:20; C. 1:18; D. 1:16 二. 填空题(本大题共 12 题,每题 4 分,满分 48 分) 7. 如果 ,53 ab 那么 ab ab 的值等于_________. 8. 抛物线 2( 1) 2yx 的顶点坐标是_________. 9. 二次函数 2 45y x x 的图像的对称轴是直线_________. 10. 计算:cot30 sin60oo_________. 11. 在某一时刻,测得一根高为 1.8m 的竹竿的影长为 3m,同时测得一根旗杆的影长为 25m, 那么这根旗杆的高度为_________m. 12. 若点 A(-3, 1y )、 B(0, 2y )是二次函数 22( 1) 1yx 图像上的两点,那么 与 的大小关系是_________(填 12yy 、 12yy 或 12yy ). 13. 如图,l1∥l2∥l3,如果 DE=6,EF=2,BC=1.5,那么 AC=_________. 14. 如图是拦水坝的横断面,斜坡 AB 的高度为 6 米,斜坡的坡比为 1:2,则斜坡 AB 的长为 _________米(保留根号). 15. 如图,正方形 ABCD 被分成 9 个全等的小正方形,P、Q 是其中两个小正方形的顶点, 设 ,,AB a AD b则向量 PQ _________(用向量 a 、b 表示). 第 13 题图 第 14 题图 第 15 题图 16. 如图,△ ABC 中,∠BAC=90°,点 G 是△ ABC 的重心,如果 AG=4,那么 BC 的长为 _________. 17. 如图,已知 4tan 3O ,点 P 在边 OA 上,OP=5,点 M、N 在边 OB 上,PM=PN,如果 MN=2,那么 PM=_________. 18. 如图,在△ ABC 中,∠ABC=90°,AB=6,BC=8.点 M、N 分别在边 AB、BC 上,沿直线 MN 将△ ABC 折叠,点 B 落在点 P 处,如果 AP∥BC 且 AP=4,那么 BN=_________. 第 16 题图 第 17 题图 第 18 题图 三. (本大题共 7 题,19-22 每题 10 分,23、24 每题 10 分,25 题 14 分,满分 78 分) 19. 已知二次函数 2y ax bx c ( ,,abc为常数,且 0a )经过 A、B、C、D 四点,其 中横坐标 x 与纵坐标 y 的对应值如下表: A B C D x -1 0 1 3 y -1 3 5 3 (1) 求二次函数的解析式; (2) 求△ ABD 的面积. 20. 如图,在等腰梯形 ABCD 中,AD∥BC,AB=DC,AC 与 BD 相交于点 O,AD:BC=1:2. (1)设 ,,BA a BC b试用 a 、b 表示 BO ; (2)先化简,再求作: 3 (2 ) 2( )2 a b a b (直接作在右图中). 21. 如图,在电线杆上的 C 处引拉线 CE、CF 固定电线杆. 拉线 CE 和地面成 60°角,在离 电线杆 6 米处安置测角仪 AB,在 A 处测得电线杆上 C 处的仰角为 23°,已知测角仪 AB 的 高为 1.5 米,求拉线 CE 的长.(已知 5 12 5sin 23 ,cos23 ,tan 23 ,13 13 12 o o o 结果保留根 号) 22. 如图,MN 经过△ ABC 的顶点 A,MN∥BC,AM=AN,MC 交 AB 于 D,NB 交 AC 于 E. (1)求证:DE∥BC; (2)联结 DE,如果 DE=1,BC=3,求 MN 的长. 1.5米 6米 EF D C B A NM ED CB A 23. 已知菱形 ABCD 中,AB=8,点 G 是对角线 BD 上一点,CG 交 BA 的延长线于点 F. (1)求证: 2 ;AG GE GF (2)如果 1 2DG GB ,且 AG⊥BF,求 cosF. 24. 已知:,如图,抛物线 2 1 :4C y ax ax c 的图像开口向上,与 x 轴交于点 A、B(A 在 B 的左边),与 y 轴交于点 C,顶点为 P,AB=2,且 OA=OC. (1)求抛物线 1C 的对称轴和函数解析式; (2)把抛物线 1C 的图像先向右平移 3 个单位,再向下平移 m 个单位得到抛物线 2C ,记 顶点为 M,并与 y 轴交于点 F(0,-1),求抛物线 2C 的函数解析式; (3)在(2)的基础上,点 G 是 y 轴上一点,当△ APF 与△ FMG 相似时,求点 G 的坐 标. G E F D CB A P C y O xBA 25. 如图,梯形 ABCD 中,AD∥BC,对角线 AC⊥BC,AD=9,AC=12,BC=16,点 E 是 边 BC 上一个动点,∠EAF=∠BAC,AF 交 CD 于点 F、交 BC 延长线于点 G. 设 BE=x. (1) 试用 x 的代数式表示 FC; (2) 设 FG yEF ,求 y 关于 x 的函数解析式,并写出定义域; (3) 当△ AEG 是等腰三角形时,直接写出 BE 的长. F GE D CB A 备用图 D CB A查看更多