- 2021-04-14 发布 |
- 37.5 KB |
- 18页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
贵阳市2021年中考数学模拟试题及答案(一)
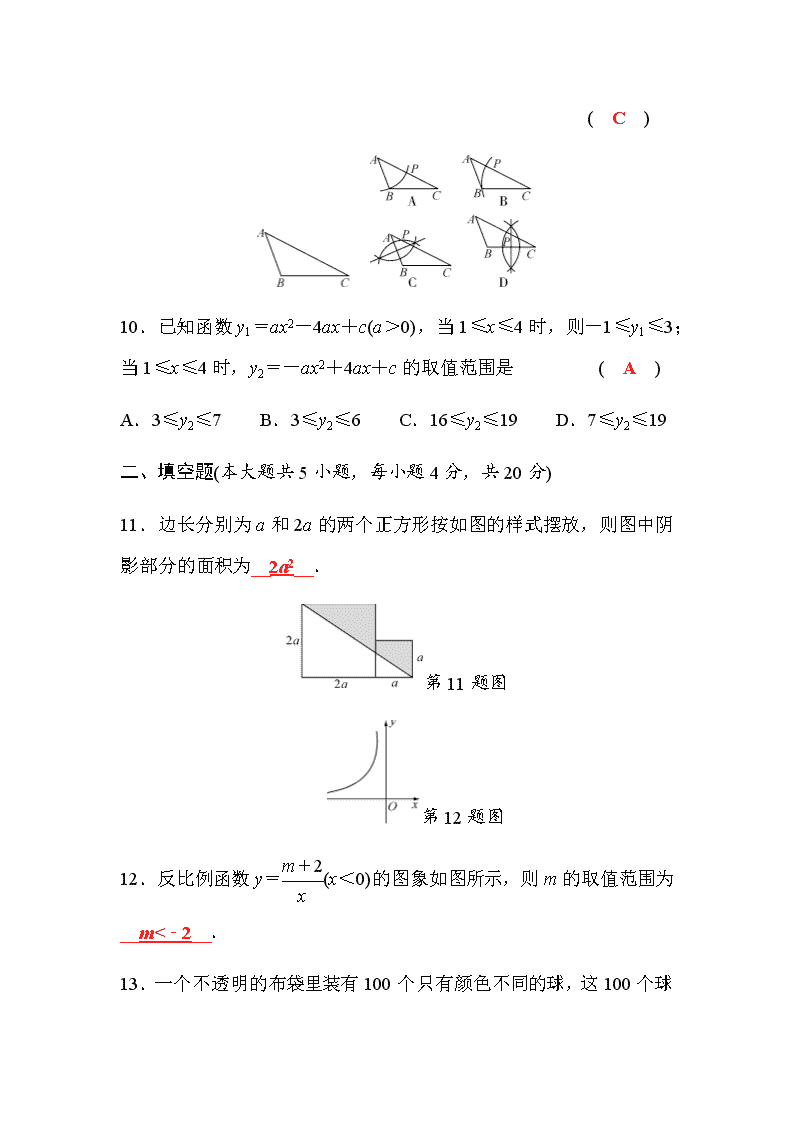
贵阳市2021年初中毕业生学业水平(升学)考试数学 模拟卷(一) (考试时间:120分钟 满分:150分) 一、选择题(本大题共10小题,每小题3分,共30分) 1.计算2×3-1的结果是 ( B ) A. B. C.1 D.2 2.下列各式中,正确的是 ( D ) A.-4-2=-2 B.3-(-3)=0 C.10+(-8)=-2 D.-5-4-(-4)=-5 3.为了解本次调研测试后我区数学学科各分数段成绩分布情况,将抽取400名同学的调研测试数学成绩进行统计分析.在这个问题中,样本是指 ( C ) A.我区2020年调研测试数学成绩 B.被抽取的400名同学 C.被抽取400名同学的调研测试数学成绩 D.400 4.如图,直线AB,CD相交于点O,∠DOF=90°,OF平分∠AOE,若∠BOD=32°,则∠DOE的度数为 ( A ) A.32° B.48° C.58° D.64° 5.要使分式有意义,则x的取值应满足 ( B ) A.x≠-2 B.x≠1 C.x=-2 D.x=1 6.在下图的四个图形中,不能由如图图形经过旋转或平移得到的是( C ) 7.下列各组条件中,能判定四边形ABCD为矩形的是 ( B ) A.∠A+∠B=90° B.AB∥CD,AB=CD,AC=BD C.AB∥CD,AD=BC,AC=BD D.AC=BD,∠A=90° 8.已知a<b,下列不等式中,变形正确的是 ( C ) A.a-3>b-3 B.> C.-3a>-3b D.3a-1>3b-1 9.如图,已知△ABC(AB<BC<AC),用尺规在AC上确定一点P,使PB+PC=AC,则下列选项中,一定符合要求的作图痕迹是 ( C ) 10.已知函数y1=ax2-4ax+c(a>0),当1≤x≤4时,则-1≤y1≤3;当1≤x≤4时,y2=-ax2+4ax+c的取值范围是 ( A ) A.3≤y2≤7 B.3≤y2≤6 C.16≤y2≤19 D.7≤y2≤19 二、填空题(本大题共5小题,每小题4分,共20分) 11.边长分别为a和2a的两个正方形按如图的样式摆放,则图中阴影部分的面积为__2a2__. 第11题图 第12题图 12.反比例函数y=(x<0)的图象如图所示,则m的取值范围为__m<-2__. 13.一个不透明的布袋里装有100个只有颜色不同的球, 这100个球中有m个红球.通过大量重复试验后发现,从布袋中随机摸出一个球,摸到红球的频率稳定在0.2左右,则m的值约为__20__. 14.设O为△ABC的内心,若∠A=48°,则∠BOC=__114__°. 15.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长为6,则AC=__3__. 三、解答题(本大题10小题,共100分) 16.(8分)(1)如图①,在Rt△ABC中,∠C=90°,AC=2,BC=1,可求得AB=______. (2)如图②,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点P(滚动时与点O重合)由原点到达点O′,则OO′的长度是______. (3)如图③,△ABC是一个等腰直角三角形,它的面积是2,把它沿着斜边的高线剪开拼成如图正方形EBDC,则这个正方形的边长是______. (4)请你在5×6的网格图④中(每个小正方形边长均为1), 画出一条长为的线段; (5)学习了实数后,我们知道数轴上的点与实数是一一对应的关系.那么请你在图⑤的数轴上画出表示-的点(保留作图痕迹). 图① 图② 图③ 图④ 图⑤ 解:(1). (2)π. (3)依题意得AC2=2,∴AC=2, ∴CD=AC=.即正方形边长是. 故答案为. (4)如图④所示,线段AB即为所求. (5)如图⑤所示. 17.(10分)小明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3 ∶4 ∶5 ∶10 ∶8,又知此次调查中捐款10元的学生一共8人. (1)小明同学调查的这组学生共有______人; (2)这组数据的众数是______元,中位数是______元; (3)若该校有2 000名学生,都进行了捐款,估计全校学生共捐款多少元? 解:(1)60. (2)20,20. (3)×2 000=38 000(元), ∴估计全校学生共捐款38 000元. 18.(10分)(2020·张家界)如图,在矩形ABCD中,过对角线BD 的中点O作BD的垂线EF,分别交AD,BC于点E,F. (1)求证:△DOE≌△BOF; (2)若AB=6,AD=8,连接BE,DF,求四边形BFDE的周长. (1)证明:∵四边形ABCD是矩形, ∴AD∥BC,DO=BO, ∴∠EDO=∠FBO, 又∵EF⊥BD, ∴∠EOD=∠FOB=90°, 在△DOE和△BOF中, ∴△DOE≌△BOF(ASA). (2)解:由(1)可得,ED∥BF,ED=BF, ∴四边形BFDE是平行四边形, ∵DO=BO,EF⊥BD, ∴EF垂直平分BD. ∴ED=EB, ∴四边形BFDE是菱形, 根据,AB=6,AD=8,设AE=x,可得BE=ED=8-x, 在Rt△ABE中,根据勾股定理可得BE2=AB2+AE2, 即(8-x)2=x2+62,解得x=, ∴BE=8-=, ∴四边形BFDE的周长=×4=25. 19.(10分)(2020·岳阳)如图,一次函数y=x+5的图象与反比例函数y=(k为常数且k≠0)的图象相交于A(-1,m),B两点. (1)求反比例函数的表达式; (2)将一次函数y=x+5的图象沿y轴向下平移b个单位(b>0),使平移后的图象与反比例函数y=的图象有且只有一个交点,求b的值. 解:(1)由题意,将点A(-1,m)代入一次函数y=x+5 得m=-1+5=4,∴A(-1,4), 将点A(-1,4)代入y=得=4,解得k=-4, 则反比例函数的表达式为y=-. (2) 将一次函数y=x+5的图象沿y轴向下平移b个单位得到的一次函数的解析式为y=x+5-b联立 整理得x2+(5-b)x+4=0, ∵一次函数y=x+5-b的图象与反比例函数y=-的图象有且只有一个交点, ∴关于x的一元二次方程x2+(5-b)x+4=0有两个相等的实数根, ∴此方程的根的判别式Δ=(5-b)2-4×4=0, 解得b1=1,b2=9,则b的值为1或9. 20.(10分)在信息化发达的今天,多媒体设备进教室已经成为学校必做的一件事情.一商城有A,B,C三种型号的甲品牌一体机和D,E两种型号的乙品牌一体机,某校准备从甲、乙两种品牌的一体机中各选择一种型号的一体机安装到各班的教室. (1)写出所有的选购方案. (2)如果所有的选购方案被选中的可能性相同,那么A 型号的一体机被选中的概率是多少? 解:(1)画树状图,如图所示. 则所有选购方案为A,D;A,E;B,D;B,E;C,D;C,E;共六种. (2)根据(1)得A型号被选中的概率P==. 21.(8分)如图,已知港口A东偏南10°方向有一处小岛B,一艘货轮从港口A沿南偏东40°航线出发,行驶80海里到达C处,此时观测小岛B在北偏东60°方向. (1)求此时货轮到小岛B的距离. (2)在小岛周围36海里范围内是暗礁区,此时货轮向正东方向航行有没有触礁危险?请作出判断并说明理由. 解:(1)由题意得,∠CAB=90°-40°-10°=40°, ∠ACB=40°+60°=100°, ∴∠B=180°-100°-40°=40°, ∴∠CAB=∠B, ∴CB=CA=80(海里), 答:此时货轮到小岛B的距离为80海里. (2)货轮向正东方向航行没有触礁危险. 理由如下:过点B作正东方向垂线交正东方向于点D, ∵∠BCD=90°-60°=30°, ∴BD=BC=40(海里), ∵40>36, ∴货轮向正东方向航行没有触礁危险. 22.(10分)为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元. (1)求键盘和鼠标的单价各是多少元; (2)经过与经销商洽谈,键盘打八折,鼠标打八五折.若学校计划购买键盘和鼠标共50个,且总费用不超过1 820元,则最多可购买键盘多少个? 解:(1)设键盘的单价为x元,鼠标的单价为y元, 根据题意得解得 答:键盘的单价为50元,鼠标的单价为40元. (2)设购买键盘m个,则购买鼠标(50-m)个, 根据题意得50×0.8m+40×0.85(50-m)≤1 820,解得m≤20. 答:最多可购买键盘20个. 23.(10分)如图,AB为⊙O的弦,OP⊥AB交⊙O于点C,垂足为点D.连接BC,∠ABC=∠PBC. (1)求证:BP是⊙O的切线; (2)若DC=3,CP=5,求AB的长. (1)证明:连接OB, ∵OB=OC, ∴∠OBC=∠OCB, ∵AB⊥OP, ∴∠OCB+∠ABC=90°, ∵∠ABC=∠PBC,∠OBC=∠OCB, ∴∠PBC+∠OBC=90°,∴OB⊥BP. ∵B是⊙O上一点,∴BP是⊙O的切线. (2)解:过点C作CE⊥BP,交BP于点E. ∵∠DBC=∠CBE,∠CDB=∠CEB,BC=BC, ∴△DBC≌△EBC(AAS), ∴BD=BE,DC=CE=3, 在Rt△CEP中,PE==4, 在Rt△DBP中,DB2+DP2=BP2. ∴DB2+64=(BD+4)2.∴DB=6, ∵OP⊥AB,∴DB=DA=6,∴AB=12. 24.(12分)(2020·青岛)为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480 m3,该游泳池有甲,乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲,乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示. (1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲,乙两个进水口的注水速度; (2)现将游泳池的水全部排空, 对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时? 解:(1)设y与t的函数解析式为y=kt+b, 解得 即y与t的函数关系式是y=140t+100, 同时打开甲,乙两个进水口的注水速度是(380-100)÷2=140(m3/h). (2)∵单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍. ∴甲进水口进水的速度是乙进水口进水速度的, ∵同时打开甲、乙两个进水口的注水速度是140 m3/h, ∴甲进水口的进水速度为 140÷×=60(m3/h),480÷60=8(h), 即单独打开甲进水口注满游泳池需8 h. 25.(12分)已知:如图,在正方形ABCD中,点E,F分别在边BC和CD上. (1)若BE=DF, ①求证:∠BAE=∠DAF; ②连接AC交EF于点O,过点F作FM∥AE,交AC的延长线于M,连接EM,求证:四边形AEMF是菱形. (2)连接BD,交AE,AF于点P,Q.若∠EAF=45°,AB=1,设BP=x,DQ=y,求y关于x的函数关系式及定义域. 图① 图② (1) 证明:①如图①中, ∵四边形ABCD是正方形, ∴∠B=∠D=90°,AB=AD, ∵BE=DF, ∴△ABE≌△ADF(SAS), ∴∠BAE=∠DAF. ②如图①中, ∵四边形ABCD是正方形, ∴∠BAC=∠DAC=45°, ∵∠BAE=∠DAF, ∴∠EAO=∠FAO, ∵△BAE≌△DAF, ∴AE=AF,∴AC⊥EF,OE=OF, ∵FM∥AE, ∴∠OFM=∠OEA, ∵∠FOM=∠EOA, ∴△FOM≌△EOA(ASA), ∴AE=FM, ∵FM∥AE, ∴四边形AEMF是平行四边形, ∵AE=AF, ∴四边形AEMF是菱形. (1) 解:如图②中,将△ADQ绕点A顺时针旋转90°得到△ABT, 连接PT. ∵△ADQ≌△ABT, ∴AQ=AT,∠ADQ=∠ABT=45°,∠DAQ=∠BAT, ∵∠ABD=45°, ∴∠TBP=90°, ∵∠EAF=45°,∠BAD=90°, ∴∠DAQ+∠BAP=∠BAT+∠BAP=45°, ∴∠PAT=∠PAQ=45°, ∵PA=PA,AT=AQ, ∴△APQ≌△APT(SAS),∴PQ=PT, ∵AB=AD=1,∠BAD=90°, ∴BD==,∴PQ=PT=-x-y, 在Rt△TBP中,∵PT2=BT2+PB2, ∴(-x-y)2=x2+y2,∴y=. ∵∠EAF=45°, ∴∠BAP≤45°.∴BP=x≤BD=.∴0≤x≤. ∴y=.查看更多