高中数学人教A版必修四全册教案1_4_1正弦、余弦函数的图象

高中数学人教A版必修四全册教案1_4_1正弦、余弦函数的图象

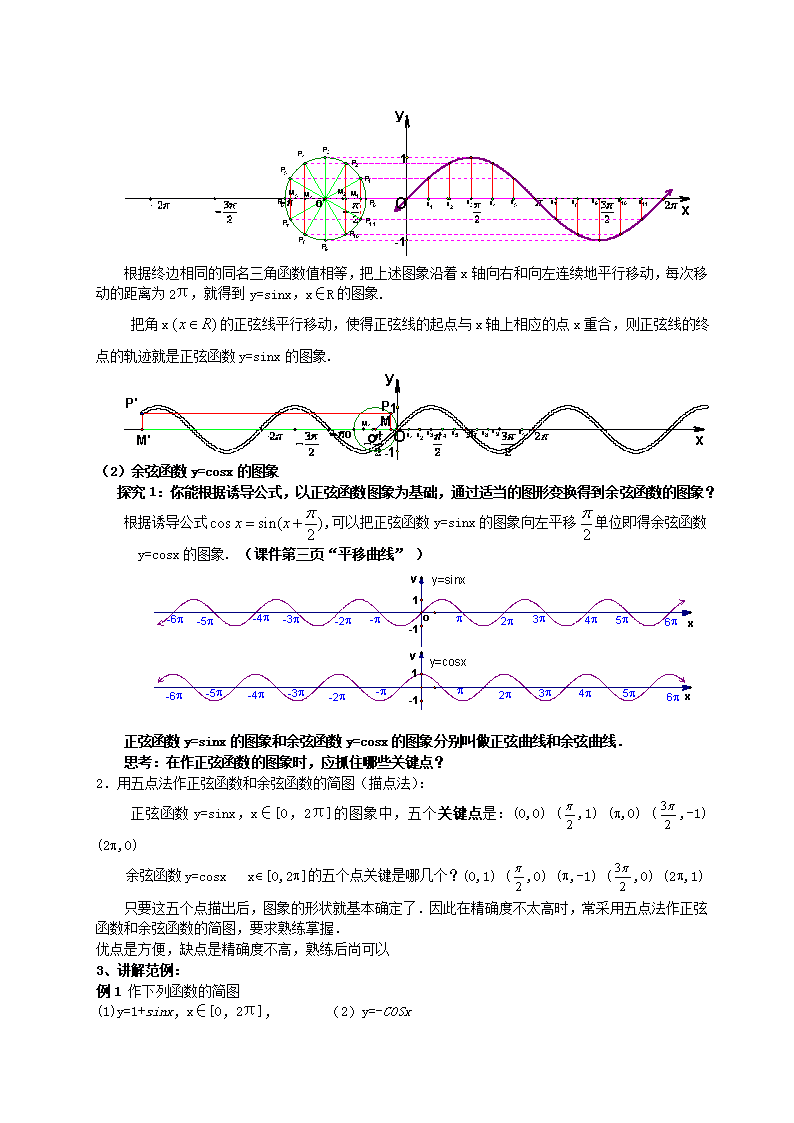
‎1.4.1正弦、余弦函数的图象 教学目的：‎ 知识目标：（1）利用单位圆中的三角函数线作出的图象，明确图象的形状；‎ ‎（2）根据关系，作出的图象；‎ ‎（3）用“五点法”作出正弦函数、余弦函数的简图，并利用图象解决一些有关问题；‎ 能力目标：（1）理解并掌握用单位圆作正弦函数、余弦函数的图象的方法；‎ ‎（2）理解并掌握用“五点法”作正弦函数、余弦函数的图象的方法； ‎ 德育目标：通过作正弦函数和余弦函数图象，培养学生认真负责，一丝不苟的学习和工作精神；‎ 教学重点：用单位圆中的正弦线作正弦函数的图象； ‎ 教学难点：作余弦函数的图象。 ‎ 教学过程：‎ 一、复习引入：‎ ‎1． 弧度定义：长度等于半径长的弧所对的圆心角称为1弧度的角。‎ ‎2.正、余弦函数定义：设是一个任意角，在的终边上任取（异于原点的）一点P（x,y）‎ P与原点的距离r()‎ 则比值叫做的正弦 记作： ‎ ‎ 比值叫做的余弦 记作： ‎ ‎3.正弦线、余弦线：设任意角α的终边与单位圆相交于点P(x，y)，过P作x轴的垂线，垂足为M，则有 ‎，‎ 向线段MP叫做角α的正弦线，有向线段OM叫做角α的余弦线．‎ 二、讲解新课： ‎ ‎1、用单位圆中的正弦线、余弦线作正弦函数、余弦函数的图象（几何法）：为了作三角函数的图象，三角函数的自变量要用弧度制来度量，使自变量与函数值都为实数．在一般情况下，两个坐标轴上所取的单位长度应该相同，否则所作曲线的形状各不相同，从而影响初学者对曲线形状的正确认识．‎ ‎（1）函数y=sinx的图象 第一步：在直角坐标系的x轴上任取一点，以为圆心作单位圆，从这个圆与x轴的交点A起把圆分成n(这里n=12)等份.把x轴上从0到2π这一段分成n(这里n=12)等份.（预备：取自变量x值—弧度制下角与实数的对应）.‎ 第二步：在单位圆中画出对应于角，，,…，2π的正弦线正弦线（等价于“列表” ）.把角x的正弦线向右平行移动，使得正弦线的起点与x轴上相应的点x重合，则正弦线的终点就是正弦函数图象上的点（等价于“描点” ）. ‎ 第三步：连线.用光滑曲线把这些正弦线的终点连结起来，就得到正弦函数y=sinx，x∈[0，2π]的图象．‎ 根据终边相同的同名三角函数值相等，把上述图象沿着x轴向右和向左连续地平行移动，每次移动的距离为2π，就得到y=sinx，x∈R的图象.‎ ‎ 把角x的正弦线平行移动，使得正弦线的起点与x轴上相应的点x重合，则正弦线的终点的轨迹就是正弦函数y=sinx的图象. ‎ ‎（2）余弦函数y=cosx的图象 ‎ 探究1：你能根据诱导公式，以正弦函数图象为基础，通过适当的图形变换得到余弦函数的图象？‎ 根据诱导公式,可以把正弦函数y=sinx的图象向左平移单位即得余弦函数y=cosx的图象. （课件第三页“平移曲线” ）‎ 正弦函数y=sinx的图象和余弦函数y=cosx的图象分别叫做正弦曲线和余弦曲线．‎ 思考：在作正弦函数的图象时，应抓住哪些关键点？‎ ‎2．用五点法作正弦函数和余弦函数的简图（描点法）：‎ 正弦函数y=sinx，x∈[0，2π]的图象中，五个关键点是：(0,0) (,1) (p,0) (,-1) (2p,0)‎ 余弦函数y=cosx xÎ[0,2p]的五个点关键是哪几个？(0,1) (,0) (p,-1) (,0) (2p,1)‎ 只要这五个点描出后，图象的形状就基本确定了．因此在精确度不太高时，常采用五点法作正弦函数和余弦函数的简图，要求熟练掌握．‎ 优点是方便，缺点是精确度不高，熟练后尚可以 ‎3、讲解范例：‎ 例1 作下列函数的简图 ‎(1)y=1+sinx，x∈[0，2π]，　 （2）y=-COSx ‎ ‎●探究2． 如何利用y=sinx，ｘ∈〔0，２π〕的图象，通过图形变换（平移、翻转等）来得到 ‎（1）y＝1＋sinx ,ｘ∈〔0，２π〕的图象；‎ ‎（2）y=sin(x- π/3)的图象？‎ 小结：函数值加减，图像上下移动；自变量加减，图像左右移动。‎ ● 探究３．‎ 如何利用y=cos x，ｘ∈〔0，２π〕的图象，通过图形变换（平移、翻转等）来得到y＝-cosx ，‎ ｘ∈〔0，２π〕的图象？ ‎ 小结：这两个图像关于X轴对称。‎ ‎●探究４． ‎ 如何利用y=cos x，ｘ∈〔0，２π〕的图象，通过图形变换（平移、翻转等）来得到y＝2-cosx ，ｘ∈〔0，２π〕的图象？‎ 小结：先作 y=cos x图象关于x轴对称的图形，得到 y＝-cosx的图象，‎ 再将y＝-cosx的图象向上平移2个单位，得到 y＝2-cosx 的图象。‎ ‎●探究５． ‎ 不用作图，你能判断函数y=sin( x - 3π/2 )和y=cosx的图象有何关系吗？请在同一坐标系中画出它们的简图，以验证你的猜想。‎ 小结：sin( x - 3π/2 )= sin[( x - 3π/2 ) +2 π] =sin(x+π/2)=cosx 这两个函数相等，图象重合。‎ 例2　分别利用函数的图象和三角函数线两种方法，求满足下列条件的x的集合：‎ ‎ ‎ 三、巩固与练习 四、小 结：本节课学习了以下内容：‎ ‎1．正弦、余弦曲线 几何画法和五点法 ‎ ‎2．注意与诱导公式，三角函数线的知识的联系 五、课后作业：《习案》作业：八