- 2021-04-14 发布 |
- 37.5 KB |
- 7页

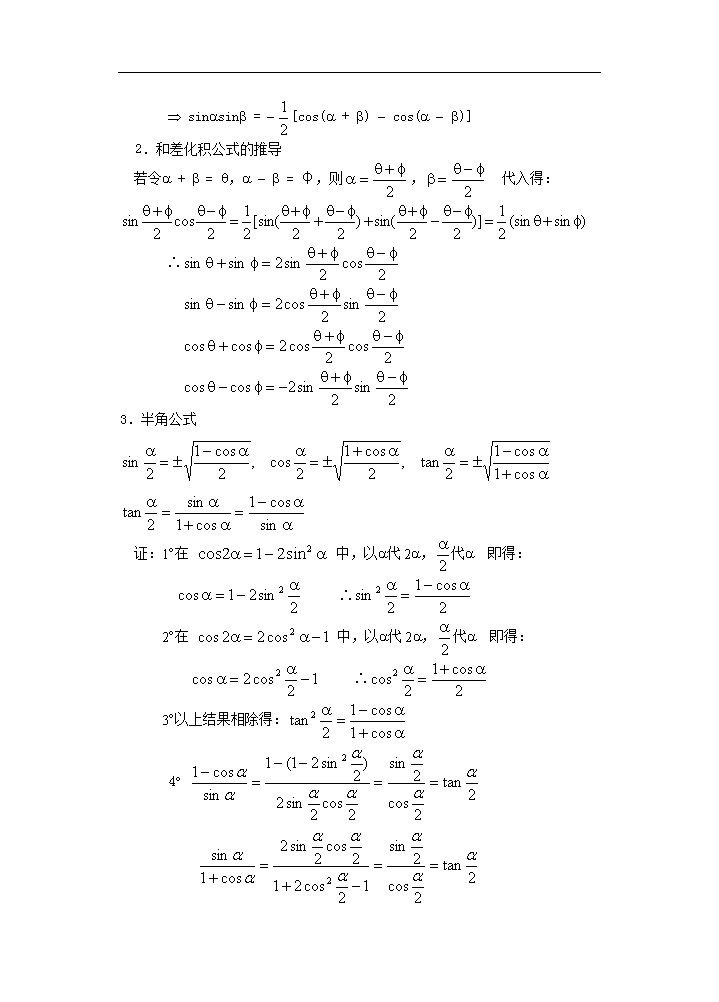

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修1教案:第四章(第21课时)两倍角的正弦余弦正切(3)
课 题:47二倍角的正弦、余弦、正切(3) 教学目的: 要求学生能较熟练地运用公式进行化简、求值、证明,增强学生灵活运用数学知识和逻辑推理能力 教学重点:二倍角公式的应用 教学难点:灵活应用和、差、倍角公式进行三角式化简、求值、证明恒等式 授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 教学过程: 一、复习引入: 二倍角公式: ; ; ; 二、讲解新课: 1.积化和差公式的推导 sin(a + b) + sin(a - b) = 2sinacosb Þ sinacosb =[sin(a + b) + sin(a - b)] sin(a + b) - sin(a - b) = 2cosasinb Þ cosasinb =[sin(a + b) - sin(a - b)] cos(a + b) + cos(a - b) = 2cosacosb Þ cosacosb =[cos(a + b) + cos(a - b)] cos(a + b) - cos(a - b) = - 2sinasinb Þ sinasinb = -[cos(a + b) - cos(a - b)] 2.和差化积公式的推导 若令a + b = q,a - b = φ,则, 代入得: ∴ 3.半角公式 证:1°在 中,以a代2a,代a 即得: ∴ 2°在 中,以a代2a,代a 即得: ∴ 3°以上结果相除得: 4° 4.万能公式 证:1° 2° 3° 三、讲解范例: 例1已知,求3cos 2q + 4sin 2q 的值 解:∵ ∴cos q ¹ 0 (否则 2 = - 5 ) ∴ 解之得:tan q = 2 ∴原式 例2已知,,tana =,tanb =,求2a + b 解: ∴ 又∵tan2a < 0,tanb < 0 ∴, ∴ ∴2a + b = 例3已知sina - cosa = ,,求和tana的值 解:∵sina - cosa = ∴ 化简得: ∴ ∵ ∴ ∴ 即 例4已知cosa - cos b = ,sina - sinb = ,求sin(a + b)的值 解:∵cosa - cos b = ,∴ ① sina - sin b =,∴ ② ∵ ∴ ∴ ∴ 例5求证:sin3asin3a + cos3acos3a = cos32a 证:左边 = (sin3asina)sin2a + (cos3acosa)cos2a = -(cos4a - cos2a)sin2a + (cos4a + cos2a)cos2a = -cos4asin2a +cos2asin2a +cos4acos2a +cos2acos2a = cos4acos2a + cos2a = cos2a(cos4a + 1) = cos2a2cos22a = cos32a = 右边 ∴原式得证 四、课堂练习: 1已知α、β为锐角,且3sin2α+2sin2β=1,3sin2α-2sin2β=0 求证:α+2β= 证法1:由已知得3sin2α=cos2β ① 3sin2α=2sin2β ② ①÷②得tanα= ∵α、β为锐角 ∴0<β<,0<2β<π,-π<-2β<0, ∴-<-2β< ∴α=-2β,α+2β= 证法2:由已知可得: 3sin2α=cos2β 3sin2α=2sin2β ∴cos(α+2β)=cosα·cos2β-sinα·sin2β =cosα·3sin2α-sinα·sin2α =3sin2αcosα-sinα·3sinαcosα=0 又由α+2β∈(0,) ∴α+2β= ① ② 证法3:由已知可得 ∴sin(α+2β)=sinαcos2β+cosαsin2β =sinα·3sin2α+cosα·sin2α =3sinα(sin2α+cos2α)=3sinα 又由②,得3sinα·cosα=sin2β ③ ①2+③2,得9sin4α+9sin2αcos2α=1 ∴sinα=,即sin(α+2β)=1 又0<α+2β< ∴α+2β= 评述:一般地,若所求角在(0,π)上,则一般取此角的余弦较为简便;若所求角在(-,)上,则一般取此角的正弦较为简便;当然,若已知条件与正切函数关系比较密切,也可考虑取此角的正切 2在△ABC中,sinA是cos(B+C)与cos(B-C)的等差中项, 试求(1)tanB+tanC的值(2)证明tanB=(1+tanC)·cot(45°+C) (1)解:△ABC中,sinA=sin(B+C) ∴2sin(B+C)=cos(B+C)+cos(B-C) ∴2sinBcosC+2cosBsinC=2cosBcosC ∵cosBcosC≠0 ∴tanB+tanC=1 (2)证明:又由上:tanβ=1-tanC=(1+tanC)· =(1+tanC)·tan(45°-C)=(1+tanC)·cot(45°+C) 3求值: 解:原式= 五、小结 通过这节课的学习,要掌握推导积化和差、和差化积公式(不要求记,半角公式和万能公式的方法,要知道它们的互化关系另外,要注意半角公式的推导与正确使用 六、课后作业: 1如果|cosθ|=,<θ<3π,则sin的值等于( ) 2设5π<θ<6π且cos=a,则sin等于( ) 3已知tan76°≈4,则tan7°的值约为( ) 4tan-cot的值等于 5已知sinA+cosA=1,0<A<π,则tan= 6已知tanα、tanβ是方程7x2-8x+1=0的两根,则tan= 7设25sin2x+sinx-24=0且x是第二象限角,求tan 8已知cos2θ=,求sin4θ+cos4θ的值 9求证 参考答案:1C 2D 3A 4-2 52- 6-2 7 8 9 七、板书设计(略) 八、课后记: 查看更多