- 2021-04-13 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修1教案:第二章(第26课时)函数应用举例4
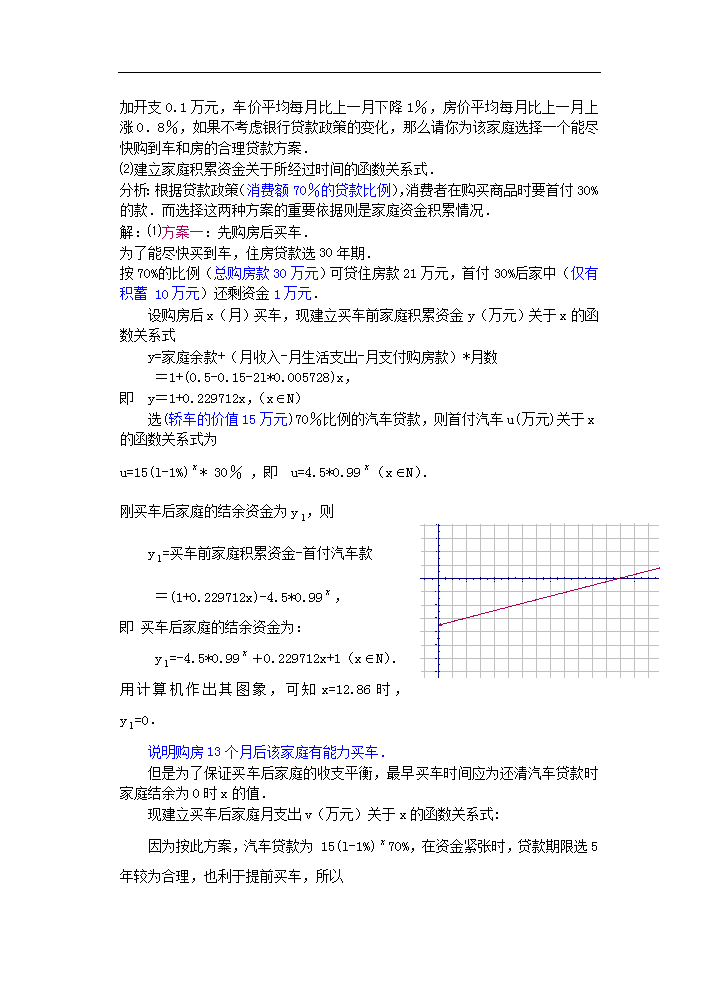
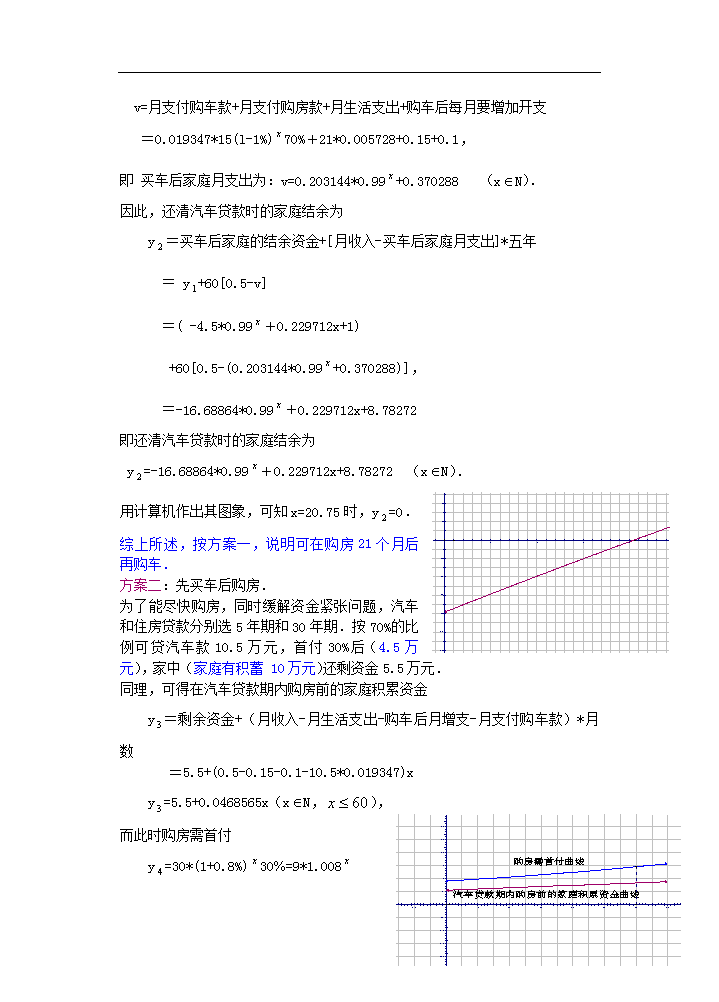
课 题:2.9.4函数应用举例4 教学目的: 1.根据实际问题,提出不同方案,建立数学模型,选定最佳方案,解决问题 2.培养培养观察分析、抽象概括、归纳总结、逻辑推理、化归转化的能力; 3.培养发现问题和提出问题的意识、善于独立思考的习惯 教学重点:数学建模的方法 教学难点:如何把实际问题抽象为数学问题. 授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 教学过程: 一、复习引入: 上一节课,我们主要学习了有关物理问题的数学模型,.这一节,我们学习有关生活消费问题的数学模型 二、新授内容: 例1随着生活质量的不断提高,购房和买车成了一些居民消费的热点.某家庭最近看中了一款价值15万元的轿车,并想在某地段购买面积为100 m,单价是0.3万元/m的一套商品房.目前,该家庭仅有积蓄 10万元,收入为 0.5万元/月,正常开支为0.15万元/月,他们准备以要购买的车、房作抵押向银行贷款,且选择消费额70%的贷款比例.表1和表2分别是1万元的住房和汽车消费贷款还本付息表. 表1(住房) 期限 年 1 2 3 4 5 6 7 8 9 10 月均还款(元) 857.50 440.10 301.10 231.70 190.13 163.75 144.08 129.38 117.99 108.92 期限 年 11 12 13 14 15 16 17 18 19 20 月均还款(元) 101.54 95.43 90.28 85.90 82.13 78.86 76 73.47 71.24 69.24 期限 年 21 22 23 24 25 26 27 28 29 30 月均还款(元) 67.45 65.85 64.40 63.08 61.89 60.80 59.80 58.89 58.05 57.28 表2(汽车) 期限(年) 1 2 3 4 5 月均还款(元) 859.98 442.94 303.95 234.99 193.47 ⑴ 现该家庭有两种贷款方案:一是马上贷款购房,等积累一定资金后再贷款买车;二是马上贷款买车,等积累一定资金后再贷款购房.如果购车后每月要增加开支0.1万元,车价平均每月比上一月下降1%,房价平均每月比上一月上涨0.8%,如果不考虑银行贷款政策的变化,那么请你为该家庭选择一个能尽快购到车和房的合理贷款方案. ⑵建立家庭积累资金关于所经过时间的函数关系式. 分析:根据贷款政策(消费额70%的贷款比例),消费者在购买商品时要首付30%的款.而选择这两种方案的重要依据则是家庭资金积累情况. 解:⑴方案一:先购房后买车. 为了能尽快买到车,住房贷款选30年期. 按70%的比例(总购房款30万元)可贷住房款21万元,首付30%后家中(仅有积蓄 10万元)还剩资金1万元. 设购房后x(月)买车,现建立买车前家庭积累资金y(万元)关于x的函数关系式 y=家庭余款+(月收入-月生活支出-月支付购房款)*月数 =1+(0.5-0.15-2l*0.005728)x, 即 y=1+0.229712x,(xN) 选(轿车的价值15万元)70%比例的汽车贷款,则首付汽车u(万元)关于x的函数关系式为 u=15(l-1%)* 30% ,即 u=4.5*0.99(xN). 刚买车后家庭的结余资金为y,则 y=买车前家庭积累资金-首付汽车款 =(1+0.229712x)-4.5*0.99, 即 买车后家庭的结余资金为: y=-4.5*0.99+0.229712x+1(xN). 用计算机作出其图象,可知x=12.86时,y=0. 说明购房13个月后该家庭有能力买车. 但是为了保证买车后家庭的收支平衡,最早买车时间应为还清汽车贷款时家庭结余为0时x的值. 现建立买车后家庭月支出v(万元)关于x的函数关系式: 因为按此方案,汽车贷款为 15(l-1%)70%,在资金紧张时,贷款期限选5年较为合理,也利于提前买车,所以 v=月支付购车款+月支付购房款+月生活支出+购车后每月要增加开支 =0.019347*15(l-1%)70%+21*0.005728+0.15+0.1, 即 买车后家庭月支出为:v=0.203144*0.99+0.370288 (xN). 因此,还清汽车贷款时的家庭结余为 y=买车后家庭的结余资金+[月收入-买车后家庭月支出]*五年 = y+60[0.5-v] =( -4.5*0.99+0.229712x+1) +60[0.5-(0.203144*0.99+0.370288)], =-16.68864*0.99+0.229712x+8.78272 即还清汽车贷款时的家庭结余为 y=-16.68864*0.99+0.229712x+8.78272 (xN). 用计算机作出其图象,可知x=20.75时,y=0. 综上所述,按方案一,说明可在购房21个月后再购车. 方案二:先买车后购房. 为了能尽快购房,同时缓解资金紧张问题,汽车和住房贷款分别选5年期和30年期.按70%的比例可贷汽车款10.5万元,首付30%后(4.5万元),家中(家庭有积蓄 10万元)还剩资金5.5万元. 同理,可得在汽车贷款期内购房前的家庭积累资金 y=剩余资金+(月收入-月生活支出-购车后月增支-月支付购车款)*月数 =5.5+(0.5-0.15-0.1-10.5*0.019347)x y=5.5+0.0468565x(xN,), 而此时购房需首付 y=30*(1+0.8%)30%=9*1.008 在同一坐标系中分别作出y、y的图像, 由图像知,在汽车贷款期内购房前的家庭积累资金一直不够购房需首付资金 也可以令x=21,则y=5.5+0.0468565%21=6.483997(万元). y=10.639315(万元) ∵10.639315(万元)>6.483997万元. ∴说明方案二购房买车所需的时间比方案一长,该方案不可取. 因此,从以上两个方案看,选择方案一才能尽快购到车和房.即先按30年期、70%的比例向银行贷款购房,21个月后再按5年期、70%的比例向银行贷款买车. 解⑵ 现建立实施方案一后的家庭积累资金y(万元)关于时间x月)的函数关系式. ①因购车前y=1+0.229712x, (xN且1查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档