- 2021-04-14 发布 |
- 37.5 KB |
- 14页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学几何综合题汇总
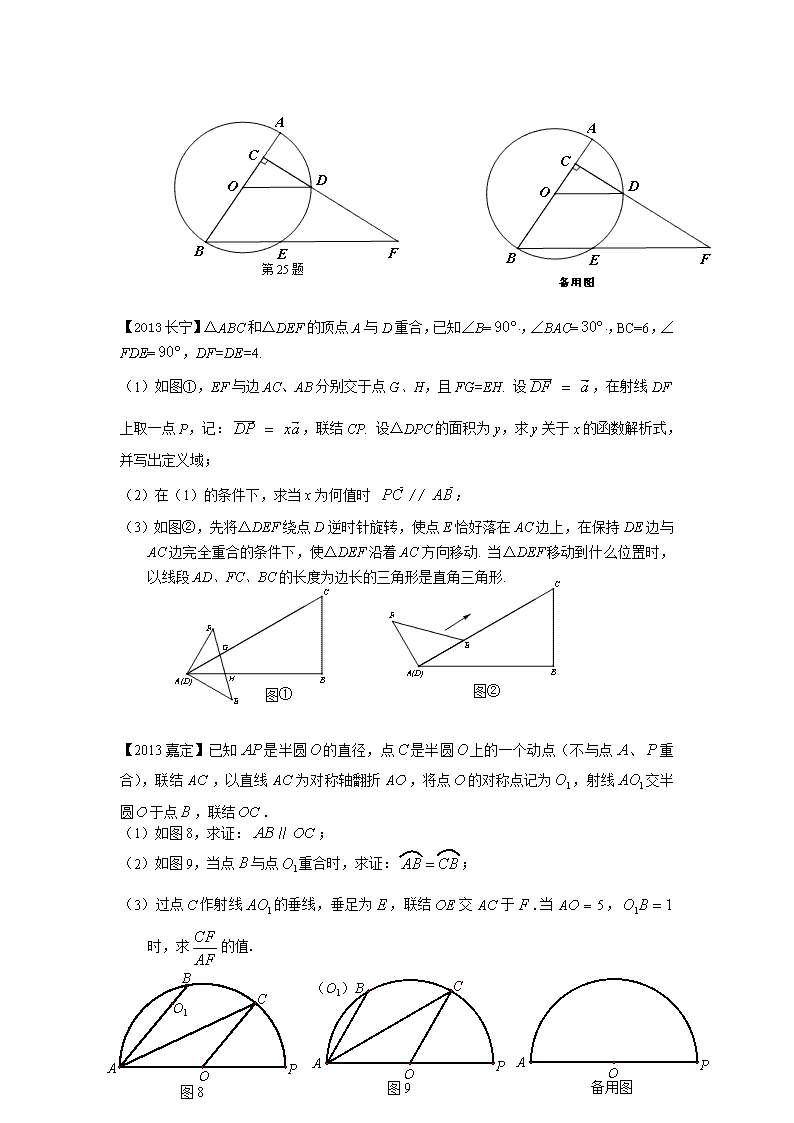
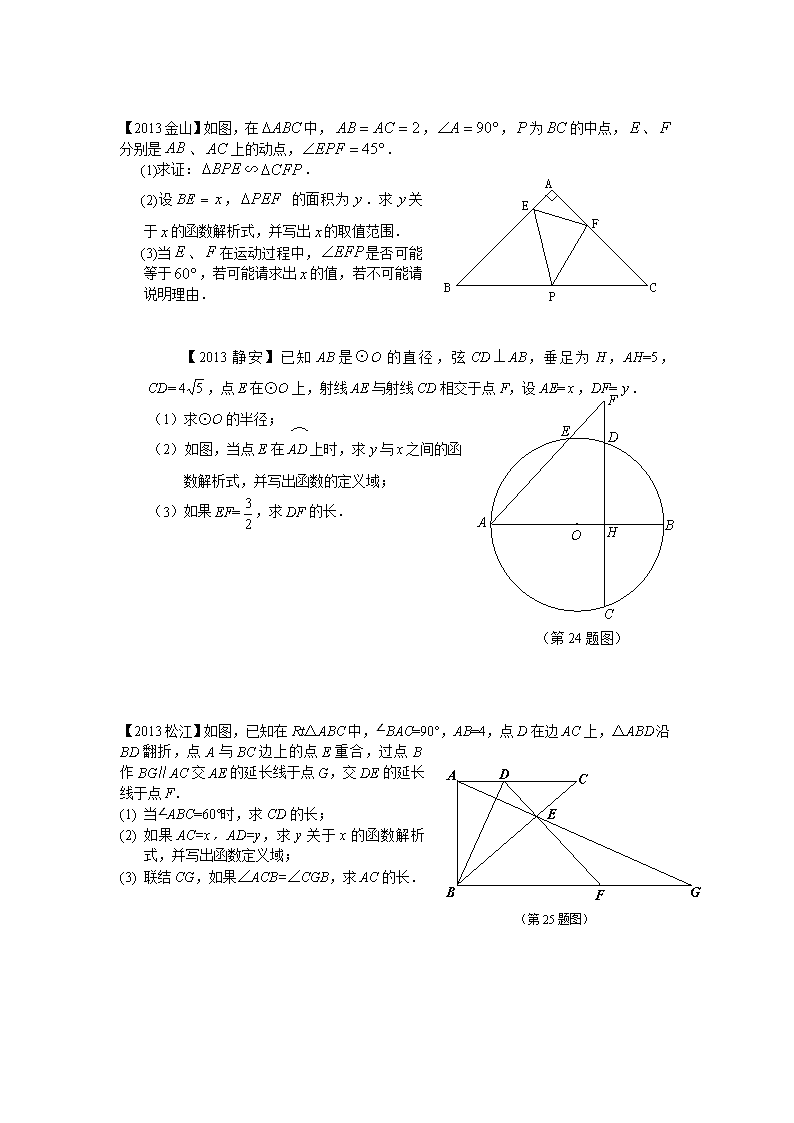
几何综合题汇总 如图8,在中,,,,点是边上任意一点,过点作交于点,截取,联结,线段交于点,设,.【2013徐汇】 (1)求关于的函数解析式及定义域; (4分) (2)如图9,联结,当和相似时,求的值; (5分) (图8) C A B D E P Q C A B D E P Q (图9) (备用图) C A B (3)当以点为圆心,为半径的⊙和以点为圆心,为半径的⊙相交的另一个交点在边上时,求的长. (5分) ⌒ ⌒ 【2013奉贤】如图,已知AB是⊙O的直径,AB=8, 点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,联结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F. (1)若 ,求∠F的度数; (2)设写出与之间的函数解析式,并写出定义域; (3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长. 第25题 【2013长宁】△ABC和△DEF的顶点A与D重合,已知∠B=.,∠BAC=.,BC=6,∠FDE=,DF=DE=4. (1)如图①,EF与边AC、AB分别交于点G、H,且FG=EH. 设,在射线DF上取一点P,记:,联结CP. 设△DPC的面积为y,求y关于x的函数解析式,并写出定义域; (2)在(1)的条件下,求当x为何值时 ; 图① 图② (3)如图②,先将△DEF绕点D逆时针旋转,使点E恰好落在AC边上,在保持DE边与AC边完全重合的条件下,使△DEF沿着AC方向移动. 当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形. 【2013嘉定】已知是半圆的直径,点是半圆上的一个动点(不与点、重合),联结,以直线为对称轴翻折,将点的对称点记为,射线交半圆于点,联结. (1)如图8,求证:∥; (2)如图9,当点与点重合时,求证:; (3)过点作射线的垂线,垂足为,联结交于.当,时,求的值. A O 备用图 P A C (O1)B O 图9 P A B C O1 O 图8 P 【2013金山】如图,在中,,,为的中点,、分别是、上的动点,. C E P F A B (1)求证:∽. (2)设, 的面积为.求关于的函数解析式,并写出的取值范围. (3)当、在运动过程中,是否可能等于,若可能请求出的值,若不可能请说明理由. 【2013静安】(第24题图) A F E D H B C O 已知AB是⊙O的直径,弦CD⊥AB,垂足为H,AH=5,CD=,点E在⊙O上,射线AE与射线CD相交于点F,设AE=,DF=. (1) 求⊙O的半径; (2) 如图,当点E在AD上时,求与之间的函 数解析式,并写出函数的定义域; (3) 如果EF=,求DF的长. 【2013松江】E A D G F B C (第25题图) 如图,已知在Rt△ABC中,∠BAC=90°,AB=4,点D在边AC上,△ABD沿BD翻折,点A与BC边上的点E重合,过点B作BG∥AC交AE的延长线于点G,交DE的延长线于点F. (1) 当∠ABC=60°时,求CD的长; (2) 如果AC=x,AD=y,求y关于x的函数解析式,并写出函数定义域; (3) 联结CG,如果∠ACB=∠CGB,求AC的长. 【2013闸北】已知:如图七,在梯形ABCD中,AD∥BC,∠A =90°,AD=6,AB=8,sinC=,点P在射线DC上, 点Q在射线AB上,且PQ⊥CD,设DP=x,BQ=y. (图八) B P A C D Q (1)求证:点D在线段BC的垂直平分线上; (2)如图八,当点P在线段DC上,且点Q在线 段AB上时,求y关于x的函数解析式,并写出定义域; (3)若以点B为圆心、BQ为半径的⊙B与以点C 为圆心、CP为半径的⊙C相切,求线段DP的长. (备用) A B C D 【2013黄浦】 如图,在梯形ABCD中,AD=BC=10,tanD=,E是腰AD上一点,且AE∶ED=1∶3. (1)当AB∶CD=1∶3时,求梯形ABCD的面积; B C D E A (2)当∠ABE=∠BCE时,求线段BE的长; (3)当△BCE是直角三角形时,求边AB的长. 【2013闵行】如图,在平行四边形ABCD中,,,CE⊥AB,垂足为点E(点E在边AB上),F为边AD的中点,联结EF,CD. (1)如图1,当点E是边AB的中点时,求线段EF的长; (2)如图2,设,△CEF的面积等于y,求y与x的函数解析式,并写出函数定义域; (3)当时,∠EFD与∠AEF的度数满足数量关系:,其中k≥0,求k的值. A B C D E F (图2) A B C D E F (图1) (第25题图) A B C D E F 【2013浦东】已知:如图,在Rt△中,,,,点在边上,以点为圆心的圆过、两点,点为上一动点. (1)求⊙的半径; (2)联结并延长,交边延长线于点,设,,求关于的函数解析式,并写出定义域; 备用图 第25题图 (3)联结,当点是AB的中点时,求△ABP的面积与△ABD的面积比的值. 【2013普陀】B P C A O Q 第25题 如图,在Rt△ABC中,∠ACB=90°,AC=6cm, BC=8cm. 点P为BC的中点,动点Q从点P出发, 延射线PC方向以2cm/s的速度运动,以点P为圆心, PQ长为半径作圆. 设点Q运动的时间为t秒, (1) 当t=1.2时,判断直线AB与⊙P的位置关系, 并说明理由;(6分) (2) 当△AQP是等腰三角形时,求t的值;(4分) (3) 已知⊙O为ABC的外接圆,若⊙P与⊙O相切, 求t的值. (4分) 【2013杨浦】 如图1,已知⊙O的半径长为3,点A是⊙O上一定点,点P为⊙O上不同于点A的动点。 (1)当时,求AP的长; (2)如果⊙Q过点P、O,且点Q在直线AP上(如图2),设AP=x,QP=y,求y关于x的函数关系式,并写出函数的定义域; (图1) (图2) (图3) (第25题图) (3)在(2)的条件下,当时(如图3),存在⊙M与⊙O相内切,同时与⊙Q相外切,且OM⊥OQ,试求⊙M的半径的长。 【2012虹口】如图,△ABC中,∠ABC=90°,AB=BC=4,点O为AB边的中点,点M是BC边上一动点(不与点B、C重合),AD⊥AB,垂足为点A.联结MO,将△BOM沿直线MO翻折,点B落在点B1处,直线M B1与AC、AD分别交于点F、N.. (1)当∠CMF=120°时,求的长; (2)设,,求关于的函数关系式,并写出自变量的取 值范围; O A B C M D N B1 F (3)联结NO,与AC边交于点E,当△FMC∽△AEO时,求的长. 第25题图 【2012宝山】已知△ABC中,(如图8),点到两边的距离相等,且PA=PB. (1)先用尺规作出符合要求的点P(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由; (2)设,,试用、的代数式表示的周长和面积; (3)设CP与AB交于点D,试探索当边AC、BC的长度变化时,的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由. A B C (备用图) A B C (图 ) 8 【2012闵行】 已知:如图,AB⊥BC,AD // BC, AB = 3,AD = 2.点P在线段AB上,联结PD,过点D作PD的垂线,与BC相交于点C.设线段AP的长为x. (1)当AP = AD时,求线段PC的长; (2)设△PDC的面积为y,求y关于x的函数解析式,并写出函数的定义域; (3)当△APD∽△DPC时,求线段BC的长. A B C D P (第25题图) A B C D (备用图) 【2012徐汇】在中,,,,⊙的半径长为1,⊙交边 于点,点是边上的动点. (1)如图8,将⊙绕点旋转得到⊙,请判断⊙与直线的位置关系; (4分) (2)如图9,在(1)的条件下,当是等腰三角形时,求的长; (5分) (3)如图10,点是边上的动点,如果以为半径的⊙和以为半径的 ⊙外切,设,,求关于的函数关系式及定义域.(5分). B O A C P 图9 B O A C P 图8 图10 O N B A C 【2012静安】O A C D B E (第25题图) 如图,⊙O的半径为6,线段AB与⊙O相交于点C、D,AC=4,∠BOD=∠A,OB与⊙O相交于点E,设OA=,CD=. (1) 求BD长; (2) 求关于的函数解析式,并写出定义域; (3) 当CE⊥OD时,求AO的长. 【2012浦东】已知:正方形ABCD的边长为1,射线AE与射线BC交于点E,射线AF与射线CD交于点F,∠EAF=45°. (1)如图1,当点E在线段BC上时,试猜想线段EF、BE、DF有怎样的数量关系?并证明你的猜想. (2)设BE=x,DF=y,当点E在线段BC上运动时(不包括点B、C),如图1,求y关于x的函数解析式,并指出x的取值范围. (3)当点E在射线BC上运动时(不含端点B),点F在射线CD上运动.试判断以E为圆心以BE为半径的⊙E和以F为圆心以FD为半径的⊙F之间的位置关系. (4)当点E在BC延长线上时,设AE与CD交于点G,如图2.问⊿EGF与⊿EFA能否相似,若能相似,求出BE的值,若不可能相似,请说明理由. 【2012市抽样】已知:在Rt△ABC中,∠C=90°,AC=4,∠A=60°,CD是边AB上的中线,直线BM∥AC,E是边CA延长线上一点,ED交直线BM于点F,将△EDC沿CD翻折得△,射线交直线BM于点G. (1)如图1,当CD⊥EF时,求BF的值; (2)如图2,当点G在点F的右侧时; ①求证:△BDF∽△BGD; ②设AE=x,△DFG的面积为y,求y关于x的函数解析式,并写出x的取值范围; (3)如果△DFG的面积为,求AE的长. (第25题图1) B A C E D F M (第25题图2) B A C E D F M G (第25题备用图) B A C D M 【2012长宁】在Rt△ABC中, AB=BC=4,∠B=,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形. (1)直角三角板绕点P旋转过程中,当BE= ▼ 时,△PEC是等腰三角形; (2)直角三角板绕点P旋转到图(1)的情形时,求证:PD =PE; (3)如图(3),若将直角三角板的直角顶点放在斜边AC的点M处,设AM : MC=m : n(m、n为正数),试判断MD、ME的数量关系,并说明理由. 图(1) 图(2) 图(3) 【2012奉贤】已知:半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B做垂线交⊙O于点C,射线PC交⊙O于点D,联结OD. (1)若AC=CD,求弦CD的长。 (2)若点C在AD上时,设PA=x,CD=y,求y与x的函数关系式及自变量x的取值范围。 B D O P A C 第25题图 (3)设CD的中点为E,射线BE与射线OD交于点F,当DF=1时,请直接写出tan∠P的值。 O A 备用图 【2012奉贤2】已知:⊙O的半径OA=5,弦AB=8,C是弦AB的中点,点P是射线AO上一点(与点A不重合),直线PC与射线BO交于点D. (1)当点P在⊙O上,求OD的长. (2)若点P在AO的延长线上,设OP=x,,求y与x的函数关系式并写出自变量x 的取值范围。 (3)连接CO,若△PCO与△PCA相似,求此时BD的长。 (第25题图) D P O C B A (备用图) O C B A (备用图) O C B A 【2012黄浦】图9 如图9,已知中,,,,是边上的中点,是边上的点(不与端点重合),是边上的点,且∥,延长与直线相交于点,点是延长线上的点,且,联结,设,. (1)求关于的函数关系式及其定义域; (2)联结,当以为半径的和以为半径的外切时,求的正切值; (3)当与相似时,求的长. 备用图b 备用图a 【2012金山】如图,中,,,过点作∥,点、分别是射线、线段上的动点,且,过点作∥交线段于点,联接,设面积为,. (1)用的代数式表示; (2)求与的函数关系式,并写出定义域; B P D Q C A O E (3)联接,若与相似,求的长. 【2012普陀】已知,,是的平分线,点P在上,.将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G. (1)如图9,当点F在射线CA上时, ①求证: PF = PE. ②设CF= x,EG=y,求y与x的函数解析式并写出函数的定义域. (2)联结EF,当△CEF与△EGP相似时,求EG的长. 图9 备用图 【2012松江】如图,在△ABC中,,,点D在AB边上(点D与点A,B不重合),DE∥BC交AC边于点E,点F在线段EC上,且,以DE、EF为邻边作平行四边形DEFG,联结BG. (1)当EF=FC时,求△ADE的面积; (2)设AE=x,△DBG的面积为y,求y与x的函数关系式,并写出x的取值范围; G E D C B A F (第25题图) (3)如果△DBG是以DB为腰的等腰三角形,求AD的值. 【2012杨浦】梯形ABCD中,AD//BC,∠ABC=α(),AB=DC=3,BC=5。点P为射线BC上动点(不与点B、C重合),点E在直线DC上,且∠APE=α。记∠PAB=∠1,∠EPC=∠2,BP=x,CE=y。 (1)当点P在线段BC上时,写出并证明∠1与∠2的数量关系; (2)随着点P的运动,(1)中得到的关于∠1与∠2的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的x的取值范围; (备用图) D C B A A B C D P E (3)若,试用x的代数式表示y。 【2012杨浦2】如图,已知:正方形ABCD中,AB=8,点O为边AB上一动点,以点O为圆心,OB为半径的⊙O交边AD于点E(不与点A、D重合),EF⊥OE交边CD于点F。设BO=x,AE=y。 (1) 求y关于x的函数关系式,并写出定义域; (2) 在点O运动的过程中,△EFD的周长是否发生变化?如果发生变化,请用x的代数式表示△EFD的周长;如果不变化,请求出△EFD的周长; (3) 以点A为圆心,OA为半径作圆,在点O运动的过程中,讨论⊙O与⊙A的位置关系,并写出相应的x的取值范围。 A B C D O E F A B C D (备用图) 查看更多