2017-2018学年山西省运城市高二下学期期中考试数学（理）试题（解析版）

2017-2018学年山西省运城市高二下学期期中考试数学（理）试题（解析版）

‎2017-2018学年山西省运城市高二下学期期中考试数学（理）试题 一、单选题 ‎1．在复平面内，复数（i为虚数单位）等于( )‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】试题分析：∴z的共轭复数，故选：A ‎【考点】复数代数形式的乘除运算．‎ ‎2．有一段“三段论”推理是这样的：‎ 对于可导函数，如果，那么是函数的极值点，因为函数在处的导数值，所以是函数的极值点.以上推理中（ ）‎ A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 结论正确 ‎【答案】A ‎【解析】试题分析：因导数函数的零点不一定都是极值点,故大前提错位,应选A．‎ ‎【考点】三段论及运用．‎ ‎3．直线与曲线在第一象限内围成的封闭图形的面积为（ ）．‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】直线与曲线的交点坐标为和，‎ 故直线与曲线在第一象限内围成的封闭图形的面积．故选．‎ ‎4．是复数为纯虚数的（ ）‎ A. 充要条件 B. 必要不充分条件 C. 充分不必要条件 D. 既不充分也不必要条件 ‎【答案】A ‎【解析】分析：由题意得到关于实数a的方程组，求解方程组即可求得最终结果.‎ 详解：若复数为纯虚数，则：‎ ‎，据此可得：.‎ 则是复数为纯虚数的充要条件.‎ 本题选择A选项.‎ 点睛：复数中，求解参数(或范围)，在数量关系上表现为约束参数的方程(或不等式).由于复数无大小之分，所以问题中的参数必为实数，因此，确定参数范围的基本思想是复数问题实数化.‎ ‎5．函数在处切线斜率为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】分析：首先求得函数的导函数，然后结合导函数研究函数的切线即可.‎ 详解：由函数的解析式可得：，‎ 则，‎ 即函数在处切线斜率为.‎ 本题选择C选项.‎ 点睛：本题主要考查导函数与原函数切线之间的关系，意在考查学生的转化能力和计算求解能力.‎ ‎6．若函数是上的单调函数，则实数的取值范围是 （ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】若函数y=x3+x2+mx+1是R上的单调函数，只需y′=3x2+2x+m≥0恒成立，即△=4﹣12m≤0，∴m≥．‎ 故选：C．‎ ‎7．对命题“正三角形的内切圆切于三边的中点”可类比猜想出：四面都为正三角形的正四面体的内切球切于四个面的什么位置？‎ A. 正三角形的顶点 B. 正三角形的中心 C. 正三角形各边的中点 D. 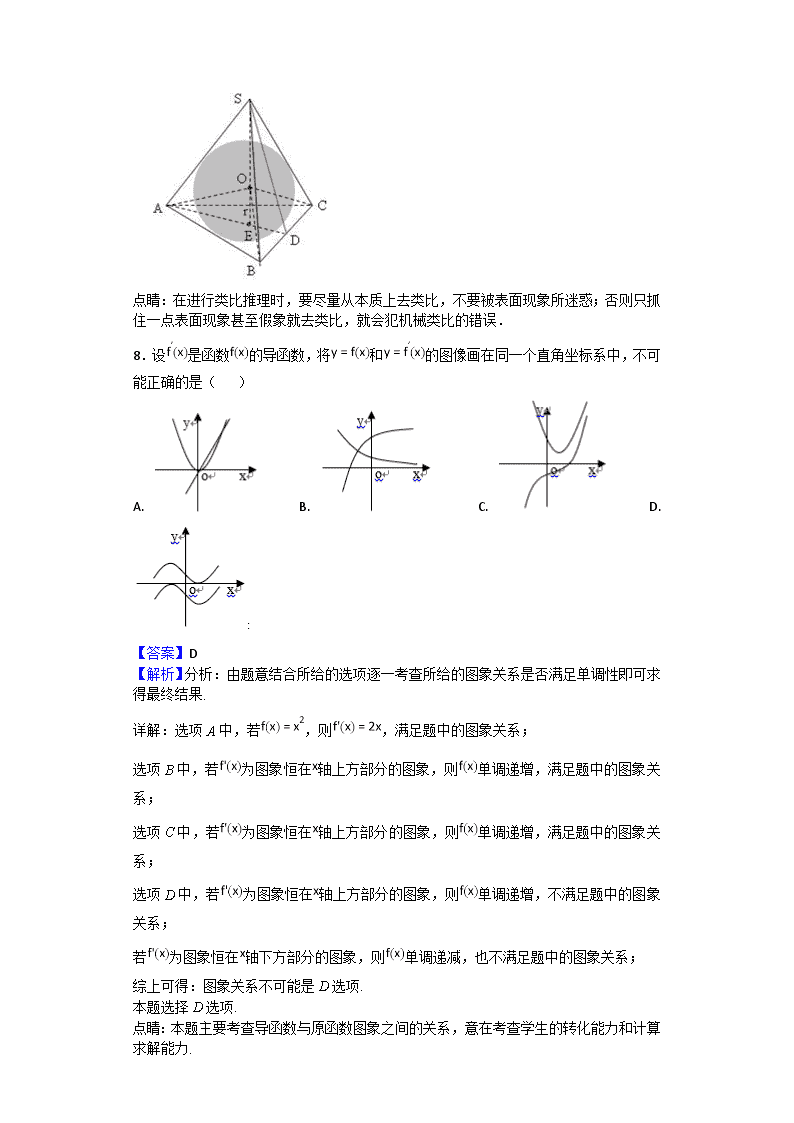无法确定 ‎【答案】B ‎【解析】分析：由题意结合几何体的空间关系进行类比推理即可求得最终结果.‎ 详解：绘制正三棱锥的内切球效果如图所示，很明显切点在面内而不在边上，则选项AC错误，由“正三角形的内切圆切于三边的中点”可类比猜想出：四面都为正三角形的正四面体的内切球切于四个面的正三角形的中心.‎ 本题选择B选项.‎ 点睛：在进行类比推理时，要尽量从本质上去类比，不要被表面现象所迷惑；否则只抓住一点表面现象甚至假象就去类比，就会犯机械类比的错误．‎ ‎8．设是函数的导函数，将和的图像画在同一个直角坐标系中，不可能正确的是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】分析：由题意结合所给的选项逐一考查所给的图象关系是否满足单调性即可求得最终结果.‎ 详解：选项A中，若，则，满足题中的图象关系；‎ 选项B中，若为图象恒在轴上方部分的图象，则单调递增，满足题中的图象关系；‎ 选项C中，若为图象恒在轴上方部分的图象，则单调递增，满足题中的图象关系；‎ 选项D中，若为图象恒在轴上方部分的图象，则单调递增，不满足题中的图象关系；‎ 若为图象恒在轴下方部分的图象，则单调递减，也不满足题中的图象关系；‎ 综上可得：图象关系不可能是D选项.‎ 本题选择D选项.‎ 点睛：本题主要考查导函数与原函数图象之间的关系，意在考查学生的转化能力和计算求解能力.‎ ‎9．函数在内有极小值，则实数的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】分析：首先求得导函数，然后结合导函数研究函数的极值，分类讨论即可求得最终结果.‎ 详解：由函数的解析式可得y′=−3x2+2a，‎ ‎∵函数y=−x3+2ax+a在(−1,0)内有极小值，‎ ‎∴令y′=−3x2+2a=0，则有一根在(−1,0)内，分类讨论：‎ a>0时，两根为，‎ 满足题意时，小根在(−1,0)内，则，即00时,令，,解得x=0或>0，列表如下：‎ ‎∵x→−∞,f(x)→−∞,而f(0)=1>0，‎ ‎∴存在x<0,使得f(x)=0,不符合条件：f(x)存在唯一的零点x0,且x0>0，应舍去。‎ 当a<0时,f′(x)=3ax2−6x=3ax(x−)=0，,解得x=0或x=<0，列表如下：‎ 而f(0)=1>0,x→+∞时,f(x)→−∞，‎ ‎∴存在x0>0,使得f(x0)=0，‎ ‎∵f(x)存在唯一的零点x0,且x0>0，‎ ‎∴极小值f()>0,化为a2>4，‎ ‎∵a<0，∴a<−2.‎ 综上可知：a的取值范围是(−∞,−2).‎ 故选：A.‎ 点睛：已知函数有零点求参数常用的方法和思路：‎ ‎（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；‎ ‎（2）分离参数法：先将参数分离，转化成函数的值域问题解决；‎ ‎（3）数形结合法：先对解析式变形，在同一个平面直角坐标系中，画出函数的图像，然后数形结合求解.‎ ‎12．已知定义在上的函数的导数为，且满足， 则（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎【解析】令g（x）= ，则g′（x） ,‎ 故g（x）在（0，+∞）递增，‎ 故g（e）＜g（e2）＜g（e3），‎ 故6f（e）＜3f（e2）＜2f（e3），‎ 故选：B．‎ 点睛：本题考查了函数的单调性问题，利用导数研究函数的单调性．考查导数的应用以及函数值的大小比较，构造新函数g（x）是解题的关键，构造函数研究新函数的单调性。本题是一道中档题． ‎ 二、填空题 ‎13．利用数学归纳法证明“， ()”时，在验证成立时，左边应该是 ．‎ ‎【答案】‎ ‎【解析】试题分析：用数学归纳法证明“， ()”时，在验证成立时，将代入，左边以1即开始，以结束，所以左边应该是.‎ ‎【考点】数学归纳法.‎ ‎14．已知为偶函数，当时，，则曲线在点处的切线方程是__________．‎ ‎【答案】‎ ‎【解析】由题意, 当时，则，,则,‎ 所以曲线在点(1,-3)处的切线的斜率,‎ 则切线方程为 ‎.‎ 点睛：导数运算及切线的理解应注意的问题 一是利用公式求导时要特别注意除法公式中分子的符号，防止与乘法公式混淆．‎ 二是直线与曲线公共点的个数不是切线的本质，直线与曲线只有一个公共点，直线不一定是曲线的切线，同样，直线是曲线的切线，则直线与曲线可能有两个或两个以上的公共点．‎ ‎15．曲线上的点到直线的最短距离是__________．‎ ‎【答案】‎ ‎【解析】试题分析：直线斜率是2，y'==2，x=，即y=ln上(,ln)处切线斜率是2‎ 所以切线是y-ln()=2(x-)，2x-y-1-ln2=0，则和2x-y+3=0的距离就是最短距离 在2x-y+3=0上任取一点(0,3)，到2x-y-1-ln2=0距离=。‎ ‎【考点】导数的几何意义。‎ ‎16．设，是的导函数，则__________．‎ ‎【答案】‎ ‎【解析】∵f（x）=sinx+2xf'（），∴f'（x）=cosx+2f'（），‎ 令x=，可得：f'（）=cos+2f'（），解得f'（）=，‎ 则f'（）=cos+2×=﹣1．‎ 故答案为：﹣1‎ 三、解答题 ‎17．（1）设复数和它的共轭复数满足：，求复数；‎ ‎（2）设复数满足：，求复数对应的点的轨迹方程.‎ ‎【答案】（1）；（2）‎ ‎【解析】分析：（1）设，由题意结合复数的运算法则可得，则，.‎ ‎（2）设复数，由题意可得，则其轨迹是椭圆，轨迹方程为：.‎ 详解：（1）设，则，‎ 由可得：，所以，‎ ‎（2）设复数，由得：，其轨迹是椭圆，此时，，，所求的轨迹方程为：.‎ 点睛：求轨迹方程时，若动点与定点、定线间的等量关系满足圆、椭圆、双曲线、抛物线的定义，则可以直接根据定义先定轨迹类型，再写出其方程，这种求轨迹方程的方法叫做定义法，其关键是准确应用解析几何中有关曲线的定义．‎ ‎18．设函数 ‎（1）讨论的单调性；‎ ‎（2）求在区间上的最大值和最小值.‎ ‎【答案】（1）见解析；（2）见解析 ‎【解析】分析：的定义域为，‎ ‎（1）由题意可得，利用导函数研究函数的单调性可得在和单调递增，在单调递减；‎ ‎（2）由（1）知，的最小值为，最大值为.‎ 详解：的定义域为，‎ ‎（1）求导函数可得：，‎ 当时，，‎ 当时，，‎ 当时，，‎ 从而在和单调递增，在单调递减；‎ ‎（2）由（1）知，在区间的最小值为，‎ 又，，最大值为.‎ 点睛：在解决类似的问题时，首先要注意区分函数最值与极值的区别．求解函数的最值时，要先求函数y＝f(x)在[a，b]内所有使f′(x)＝0的点，再计算函数y＝f(x)在区间内所有使f′(x)＝0的点和区间端点处的函数值，最后比较即得．‎ ‎19．观察下列方程，并回答问题：‎ ‎①；②；③；④；…‎ ‎(1)请你根据这列方程的特点写出第个方程；‎ ‎(2)直接写出第2009个方程的根；‎ ‎(3)说出这列方程的根的一个共同特点.‎ ‎【答案】（1）（2）1，-2009.（3）方程的根共有两个，一个是1，一个是.‎ ‎【解析】试题分析：（1）根据方程特点：二次项系数为1，一次项系数及常数项依次成等差数列，即第个方程为： .（2）由方程因式分解得第2009个方程的根为：1，-2009. (3) 这列方程的根一个是1，一个是.‎ 试题解析：(1)由已知方程：‎ ‎①；‎ ‎②；‎ ‎③；‎ ‎④；‎ 归纳可得，第个方程为： .‎ 第2009个方程为： ，‎ 此方程可化为： ，‎ 故第2009个方程的根为：1，-2009.‎ ‎(3)这列方程的根共有两个，一个是1，一个是.‎ ‎20．已知函数．‎ ‎（1）当时，求函数在上的最大值和最小值；‎ ‎（2）函数既有极大值又有极小值，求实数的取值范围．‎ ‎【答案】（1）最大值是，最小值为；（2）．‎ ‎【解析】试题分析：（1）把代入到中，求出导函数时的值为，得到函数的极大值为，然后判断和谁小谁为最小值即可；（2）若既有极大值又有极小值，首先必须有两个不同正根，即有两个不同正根，有二次函数根的分布可知，应满足，解不等式从而可得实数的取值范围．‎ 试题解析：（1）时，，‎ 函数在区间仅有极大值点，故这个极大值点也是最大值点，‎ 故函数在最大值是， ‎ 又，故．‎ 故函数在上的最小值为． ‎ ‎（2）‎ 若既有极大值又有极小值，则首先必须有两个不同正根，即有两个不同正根，故应满足． ‎ ‎【考点】1、利用导数求函数闭区间上的最值；2、利用导数研究函数的单调性及函数在某点取极值的条件．‎ ‎【方法点睛】本题主要考查利用导数求函数极值和最值，属于难题. 求函数极值的步骤：（1）确定函数的定义域；（2）求导数；（3）解方程求出函数定义域内的所有根；（4）列表检查在的根左右两侧值的符号，如果左正右负，那么在处取极大值，如果左负右正，那么在处取极小值, 如果在点 的左右两侧符号不变，则不是函数极值,最后再比较端点处的函数值与极大值极小值的大小，就可得到函数在闭区间上的最值.‎ ‎21．已知是定义在上的奇函数，当时，，且曲线在处的切线与直线平行．‎ ‎（Ⅰ）求的值及函数的解析式；‎ ‎（Ⅱ）若函数在区间上有三个零点，求实数的取值范围．‎ ‎【答案】（Ⅰ），；（Ⅱ）．‎ ‎【解析】试题分析：（Ⅰ）首先求得导函数，然后利用导数的几何意义结合两直线平行的关系求得的值，由此求得函数的解析式；（Ⅱ）将问题转化为函数的图象与有三个公共点，由此结合图象求得的取值范围．‎ 试题解析：（Ⅰ）当时，，‎ 因为曲线在处的切线与直线平行，‎ 所以，解得，‎ 所以．‎ ‎（Ⅱ）由（Ⅰ）知，，，，‎ 所以函数在区间上有三个零点，‎ 等价于函数在上的图象与有三个公共点．‎ 结合函数在区间上大致图象可知，实数的取值范围是．‎ ‎【考点】1、导数几何意义；2、函数的零点；3、函数的图象．‎ ‎【知识点睛】对于函数零点的判定：如果函数在区间上的图象是连续不断的一条曲线,并且有，那么函数在区间内有零点,即存在，使得，这个也就是方程的根．‎ ‎22．设函数．‎ ‎（1）若函数在上为减函数，求实数的最小值；‎ ‎（2）若存在，使成立，求实数的取值范围．‎ ‎【答案】（Ⅰ）最小值为；（II）‎ ‎【解析】试题分析： 在上为减函数，等价于在上恒成立，进而转化为，根据二次函数的性质可得 命题“若存在, ，使成立”等价于 ‎“当时，有 ”， 由易求，从而问题等价于“当时，有”，分 , 两种情况讨论:‎ 当是易求，当时可求得的值域为，再按 两种情况讨论即可 解析：（1）由已知得， ‎ 因在上为减函数，故在上恒成立。‎ 所以当时。‎ 又， ‎ 故当时，即时， .‎ 所以，于是，故的最小值为. ‎ ‎（2）命题“若存在, ，使成立”等价于 ‎“当时，” ”， ‎ 由（1），当时， ， .‎ 问题等价于：“当时，有”. ‎ 当，由（1），在为减函数，‎ 则，故. ‎ 当时，由于在上的值域为 ‎（i），即， 在恒成立，故在上为增函数，‎ 于是， ，矛盾。 ‎ ‎（ii），即，由的单调性和值域知，‎ 存在唯一，使，且满足：‎ 当时， ， 为减函数；当时， ， 为增函数；‎ 所以， ， ‎ 所以， ，与矛盾。‎ 综上得 ‎ 点睛：遇到““若存在, ，使成立””的条件是要进行转化，转化为最值之间的不等关系，利用导数性质结合分类讨论，求出结果。题目可以改编“若任意，使成立”则等价于“”‎