2018人教A版数学必修二1.3《空间几何体的表面积与体积》学案1

2018人教A版数学必修二1.3《空间几何体的表面积与体积》学案1

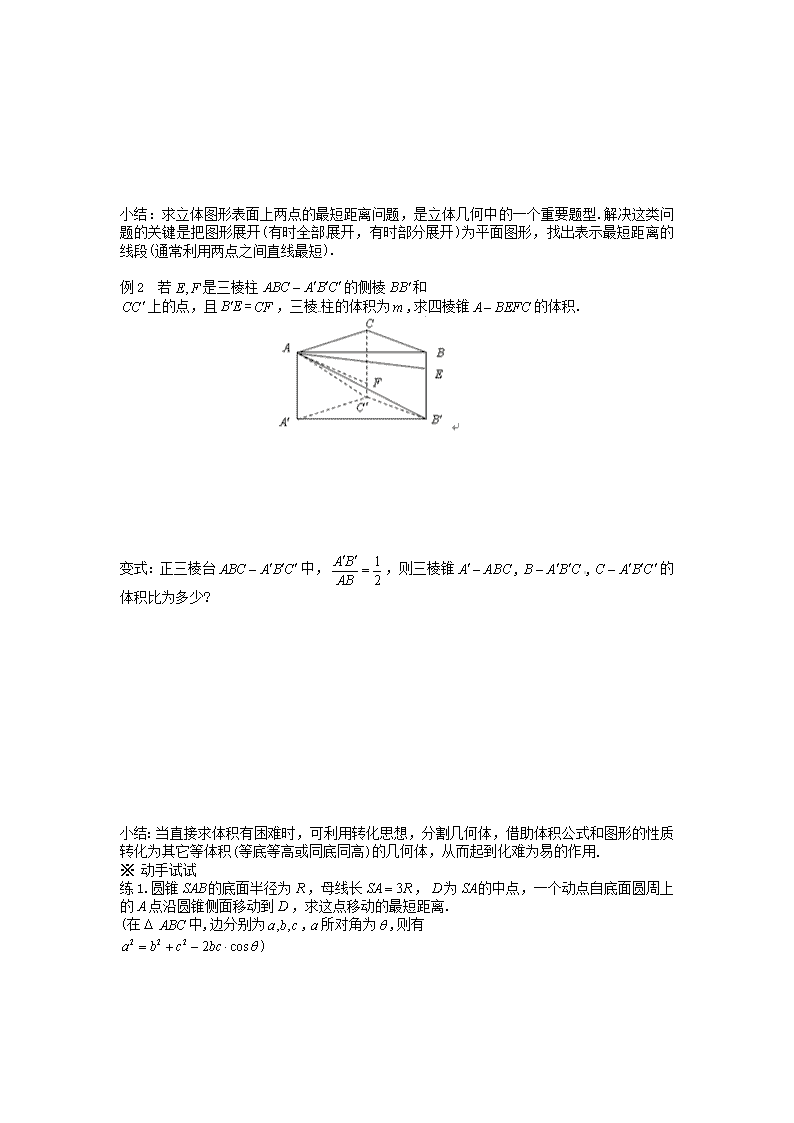
高中数学《1.3空间几何体的表面积与体积》学案 新人教A版必修2‎ ‎ 学习目标 ‎ ‎1. 会求空间几何体、简单组合体的面积和体积；‎ ‎2. 能解决与空间几何体表面积、体积有关的综合问题；‎ ‎3. 进一步体会把空间问题转化为平面问题的思想.‎ ‎ 学习过程 ‎ 一、课前准备 ‎（复习教材P23~ P28，找出疑惑之处）‎ 复习1：柱体、锥体、台体的表面积是如何求出来的？它们的体积公式有何联系？球的表面积和体积只和什么变量有关？‎ 复习2：简单组合体的表面积和体积怎么求？‎ 二、新课导学 ‎※ 典型例题 例1 设圆台的上、下底面半径分别为,，母线长是，圆台侧面展开后所得的扇环的圆心角是，求证：（度）‎ 小结：有关几何体侧面的问题，通常是把侧面展开为平面图形，然后在平面图形中寻求解决途径.‎ 变式：在长方体中,已知,‎ ‎,从点出发,沿着表面运动到,则最短路线长是多少?‎ 小结：求立体图形表面上两点的最短距离问题，是立体几何中的一个重要题型.解决这类问题的关键是把图形展开(有时全部展开，有时部分展开)为平面图形，找出表示最短距离的线段(通常利用两点之间直线最短).‎ 例2 若是三棱柱的侧棱和 上的点，且=，三棱柱的体积为,求四棱锥的体积.‎ 变式：正三棱台中，，则三棱锥,,的体积比为多少?‎ 小结：当直接求体积有困难时，可利用转化思想，分割几何体，借助体积公式和图形的性质转化为其它等体积(等底等高或同底同高)的几何体，从而起到化难为易的作用.‎ ‎※ 动手试试 练1. 圆锥的底面半径为，母线长，为的中点，一个动点自底面圆周上的点沿圆锥侧面移动到，求这点移动的最短距离.‎ ‎(在中,边分别为,所对角为,则有 ‎)‎ 练2. 直三棱柱各侧棱和底面边长均为，点是 上任意一点，连结、、、，则三棱锥—的体积为多少？ （ ）‎ ‎ ‎ 三、总结提升 ‎※ 学习小结 ‎1. 空间问题可以转化为平面问题解决；‎ ‎2. 最短距离的求法；‎ ‎3. 求体积困难时可采用分割的思想，化为底（面积）高相同的规则几何体求解.‎ ‎※ 知识拓展 空间问题向平面的转化包括：圆锥、圆台中元素的关系问题，用轴截面来解决；空间几何体表面上两点线路最短问题，用侧面展开图来解决；球的组合体中的切、接问题，用过球心的截面来解决.‎ ‎ 学习评价 ‎ ‎※ 自我评价 你完成本节导学案的情况为（ ）.‎ ‎ A. 很好 B. 较好 C. 一般 D. 较差 ‎※ 当堂检测（时量：5分钟 满分：10分）计分：‎ ‎1. 在棱长为的正方体上，分别用过顶点的三条棱中点的平面截该正方体，则截去个三棱锥后，剩下多面体的体积为（ ）.‎ ‎ A. B. C. D.‎ ‎2. 已知球面上过三点的截面和球心的距离是球半径的一半，且，则球的表面积为（ ）.‎ A. B. C. D.‎ ‎3. 正方体的8个顶点中有4个恰为正四面体的顶点,则正方体的全面积与正四面体的全面积之比为（ ）.‎ ‎ A. B. C. D.‎ ‎4. 正四棱锥底面积为，过两对侧棱的截面面积为 ‎，则棱锥的体积为___________.‎ ‎5. 已知圆锥的全面积是底面积的倍，那么该圆锥的侧面展开图的圆心角______度. ‎ ‎ 课后作业 ‎ ‎1. 一个圆台上下底面半径分别为5、10，母线=‎ ‎20.一只蚂蚁从的中点绕圆台侧面转到下底面圆周上的点，求蚂蚁爬过的最短距离.‎ ‎2. 已知一个圆锥的底面半径为,高为,在其中有个高为的内接圆柱.‎ (1) 求圆柱的侧面积；‎ (2) 为何值时，圆柱的侧面积最大？‎