2020年全国中考数学试卷分类汇编(一)专题22 等腰三角形(含解析)

2020年全国中考数学试卷分类汇编(一)专题22 等腰三角形(含解析)

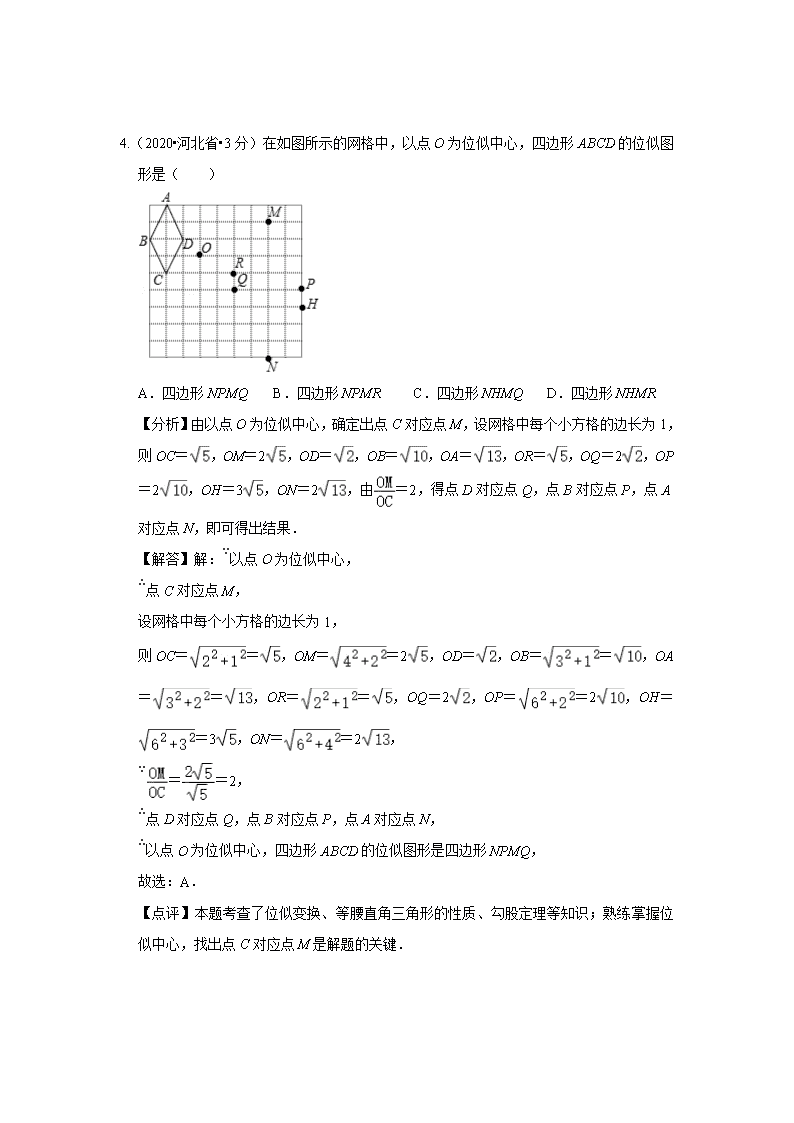
等腰三角形 ‎ 一.选择题 ‎1. （2020年辽宁省辽阳市）4．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．‎ ‎【解答】解：A.是轴对称图形，不是中心对称图形，故本选项不合题意；‎ B.既不是轴对称图形，也不是中心对称图形，故本选项不合题意；‎ C.是轴对称图形，不是中心对称图形，故本选项不合题意；‎ D.既是轴对称图形又是中心对称图形，故本选项符合题意．‎ 故选：D．‎ ‎【点评】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．‎ ‎2.（2020•河南省•3分）如图，在△ABC中，AB＝BC＝，∠BAC＝30°，分别以点A，C为圆心，AC的长为半径作弧，两弧交于点D，连接DA，DC，则四边形ABCD的面积为（　　）‎ A．6 B．9 C．6 D．3‎ ‎【分析】连接BD交AC于O，根据已知条件得到BD垂直平分AC，求得BD⊥AC，AO＝CO，根据等腰三角形的性质得到∠ACB＝∠BAC＝30°，根据等边三角形的性质得到∠DAC ‎＝∠DCA＝60°，求得AD＝CD＝AB＝3，于是得到结论．‎ ‎【解答】解：连接BD交AC于O，‎ ‎∵AD＝CD，AB＝BC，‎ ‎∴BD垂直平分AC，‎ ‎∴BD⊥AC，AO＝CO，‎ ‎∵AB＝BC，‎ ‎∴∠ACB＝∠BAC＝30°，‎ ‎∵AC＝AD＝CD，‎ ‎∴△ACD是等边三角形，‎ ‎∴∠DAC＝∠DCA＝60°，‎ ‎∴∠BAD＝∠BCD＝90°，∠ADB＝∠CDB＝30°，‎ ‎∵AB＝BC＝，‎ ‎∴AD＝CD＝AB＝3，‎ ‎∴四边形ABCD的面积＝2×＝3，‎ 故选：D．‎ ‎【点评】本题考查了含30°角的直角三角形，等腰三角形的性质，等边三角形的判定和性质，熟练掌握直角三角形的性质是解题的关键．‎ ‎3.（2020•贵州省铜仁市•4分）已知等边三角形一边上的高为2，则它的边长为（　　）‎ A．2 B．3 C．4 D．4‎ ‎【分析】根据等边三角形的性质：三线合一，利用勾股定理可求解即可．‎ ‎【解答】解：根据等边三角形：三线合一，‎ 设它的边长为x，可得：，‎ 解得：x＝4，x＝﹣4（舍去），‎ 故选：C．‎ ‎4.（2020•河北省•3分）在如图所示的网格中，以点O为位似中心，四边形ABCD的位似图形是（　　）‎ A．四边形NPMQ B．四边形NPMR C．四边形NHMQ D．四边形NHMR ‎【分析】由以点O为位似中心，确定出点C对应点M，设网格中每个小方格的边长为1，则OC＝，OM＝2，OD＝，OB＝，OA＝，OR＝，OQ＝2，OP＝2，OH＝3，ON＝2，由＝2，得点D对应点Q，点B对应点P，点A对应点N，即可得出结果．‎ ‎【解答】解：∵以点O为位似中心，‎ ‎∴点C对应点M，‎ 设网格中每个小方格的边长为1，‎ 则OC＝＝，OM＝＝2，OD＝，OB＝＝，OA＝＝，OR＝＝，OQ＝2，OP＝＝2，OH＝＝3，ON＝＝2，‎ ‎∵＝＝2，‎ ‎∴点D对应点Q，点B对应点P，点A对应点N，‎ ‎∴以点O为位似中心，四边形ABCD的位似图形是四边形NPMQ，‎ 故选：A．‎ ‎【点评】本题考查了位似变换、等腰直角三角形的性质、勾股定理等知识；熟练掌握位似中心，找出点C对应点M是解题的关键．‎ ‎5. (2020•江苏省无锡市•3分)如图，等边△ABC的边长为3，点D在边AC上，AD＝，线段PQ在边BA上运动，PQ＝，有下列结论：‎ ‎①CP与QD可能相等；②△AQD与△BCP可能相似；‎ ‎③四边形PCDQ面积的最大值为；④四边形PCDQ周长的最小值为3+．‎ 其中，正确结论的序号为(　　)‎ A．①④ B．②④ C．①③ D．②③‎ ‎【分析】①利用图象法判断即可．‎ ‎②当∠ADQ＝∠CPB时，△ADQ∽△BPC．‎ ‎③设AQ＝x，则四边形PCDQ的面积＝×32－×x××－×3×(3－x－)×＝+x，当x取最大值时，可得结论．‎ ‎④如图，作点D关于AB的对称点D′，作D′F∥PQ，使得D′F＝PQ，连接CF交AB于点P′，此时四边形P′CD′Q′的周长最小．求出CF的长即可判断．‎ ‎【解答】解：①利用图象法可知PC＞DQ，故①错误．‎ ‎②∵∠A＝∠B＝60°，∴当∠ADQ＝∠CPB时，△ADQ∽△BPC，故②正确．‎ ‎③设AQ＝x，则四边形PCDQ的面积＝×32－×x××－×3×(3－x－)×＝+x，∵x的最大值为3－＝，∴x＝时，四边形PCDQ的面积最大，最大值＝，故③正确，‎ 如图，作点D关于AB的对称点D′，作D′F∥PQ，使得D′F＝PQ，连接CF交AB于点P′，此时四边形P′CD′Q′的周长最小．‎ 过点C作CH⊥D′F交D′F的延长线于H，交AB于J．‎ 由题意，DD′＝2AD•sin60°＝，HJ＝DD′＝，CJ＝，FH＝－－＝，‎ ‎∴CH＝CJ+HJ＝，∴CF＝＝＝，‎ ‎∴四边形P′CDQ′的周长的最小值＝3+，故④错误，故选：D．‎ ‎【点评】本题考查相似三角形的判定和性质，一次函数的性质，轴对称最短问题等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．‎ ‎ ‎ 二.填空题 ‎1.（2020•贵州省贵阳市•4分）如图，△ABC是⊙O的内接正三角形，点O是圆心，点D，E分别在边AC，AB上，若DA＝EB，则∠DOE的度数是　120　度．‎ ‎【分析】连接OA，OB，根据已知条件得到∠AOB＝120°，根据等腰三角形的性质得到∠OAB＝∠OBA＝30°，根据全等三角形的性质得到∠DOA＝∠BOE，于是得到结论．‎ ‎【解答】解：连接OA，OB，‎ ‎∵△ABC是⊙O的内接正三角形，‎ ‎∴∠AOB＝120°，‎ ‎∵OA＝OB，‎ ‎∴∠OAB＝∠OBA＝30°，‎ ‎∵∠CAB＝60°，‎ ‎∴∠OAD＝30°，‎ ‎∴∠OAD＝∠OBE，‎ ‎∵AD＝BE，‎ ‎∴△OAD≌△OBE（SAS），‎ ‎∴∠DOA＝∠BOE，‎ ‎∴∠DOE＝∠DOA+∠AOE＝∠AOB＝∠AOE+∠BOD＝120°，‎ 故答案为：120．‎ ‎【点评】本题考查了三角形的外接圆与外心，等边三角形的性质，全等三角形的判定和性质，正确的作出辅助线构造全等三角形是解题的关键．‎ ‎2.（2020•贵州省贵阳市•4分）如图，△ABC中，点E在边AC上，EB＝EA，∠A＝2∠CBE，CD垂直于BE的延长线于点D，BD＝8，AC＝11，则边BC的长为　4　．‎ ‎【分析】延长BD到F，使得DF＝BD，根据等腰三角形的性质与判定，勾股定理即可求出答案．‎ ‎【解答】解：延长BD到F，使得DF＝BD，‎ ‎∵CD⊥BF，‎ ‎∴△BCF是等腰三角形，‎ ‎∴BC＝CF，‎ 过点C点作CH∥AB，交BF于点H ‎∴∠ABD＝∠CHD＝2∠CBD＝2∠F，‎ ‎∴HF＝HC，‎ ‎∵BD＝8，AC＝11，‎ ‎∴DH＝BH﹣BD＝AC﹣BD＝3，‎ ‎∴HF＝HC＝8﹣3＝5，‎ 在Rt△CDH，‎ ‎∴由勾股定理可知：CD＝4，‎ 在Rt△BCD中，‎ ‎∴BC＝＝4，‎ 故答案为：4‎ ‎【点评】本题考查勾股定理，解题的关键是熟练运用等腰三角形的性质与判定，本题属于中等题型．‎ ‎3. （2020年滨州市）14．（5分）在等腰△ABC中，AB＝AC，∠B＝50°，则∠A的大小为　80°　．‎ ‎【分析】根据等腰三角形两底角相等可求∠C，再根据三角形内角和为180°列式进行计算即可得解．‎ ‎【解答】解：∵AB＝AC，∠B＝50°，‎ ‎∴∠C＝∠B＝50°，‎ ‎∴∠A＝180°﹣2×50°＝80°．‎ 故答案为：80°．‎ ‎【点评】本题考查了等腰三角形的性质，主要利用了等腰三角形两底角相等的性质．‎ ‎4. （2020•江苏省常州市•2分）如图，在△ABC中，BC的垂直平分线分别交BC.AB于点E.F．若△AFC是等边三角形，则∠B＝　30　°．‎ ‎【分析】根据垂直平分线的性质得到∠B＝∠BCF，再利用等边三角形的性质得到∠AFC＝60°，从而可得∠B的度数．‎ ‎【解答】解：∵EF垂直平分BC，‎ ‎∴BF＝CF，‎ ‎∴∠B＝∠BCF，‎ ‎∵△ACF为等边三角形，‎ ‎∴∠AFC＝60°，‎ ‎∴∠B＝∠BCF＝30°．‎ 故答案为：30．‎ ‎【点评】本题考查了垂直平分线的性质，等边三角形的性质，三角形外角的性质，解题的关键是利用垂直平分线的性质得到∠B＝∠BCF．‎ ‎5. （2020•江苏省淮安市•3分）如图，等腰△ABC的两个顶点A（﹣1，﹣4）、B（﹣4，﹣1）在反比例函数y＝（x＜0）的图象上，AC＝BC．过点C作边AB的垂线交反比例函数y＝（x＜0）的图象于点D，动点P从点D出发，沿射线CD方向运动3个单位长度，到达反比例函数y＝（x＞0）图象上一点，则k2＝　1　．‎ ‎【分析】用待定系数求得反比例函数y＝，再与直线y＝x联立方程组求得D点坐标，再题意求得运动后P点的坐标，最后将求得的P点坐标代入y＝（x＞0）求得结果．‎ ‎【解答】解：把A（﹣1，﹣4）代入y＝中得，k1＝4，‎ ‎∴反比例函数y＝为，‎ ‎∵A（﹣1，﹣4）、B（﹣4，﹣1），‎ ‎∴AB的垂直平分线为y＝x，‎ 联立方程驵，解得，或，‎ ‎∵AC＝BC，CD⊥AB，‎ ‎∴CD是AB的垂直平分线，‎ ‎∵CD与反比例函数y＝（x＜0）的图象于点D，‎ ‎∴D（﹣2，﹣2），‎ ‎∵动点P从点D出发，沿射线CD方向运动3个单位长度，到达反比例函数y＝（x＞0）图象上一点，‎ ‎∴设移动后的点P的坐标为（m，m）（m＞﹣2），则 ‎＝（3）2，‎ ‎∴m＝1，‎ ‎∴P（1，1），‎ 把P（1，1）代入y＝（x＞0）中，得k2＝1，‎ 故答案为：1．‎ ‎【点评】本题主要考查了反比例函数的图象与性质，等腰三角形的性质，求反比例函数图象与一次函数图象的交点坐标，待定系数法，关键是确定直线CD的解析式．‎ ‎6. （2020•江苏省南京市•2分）如图，线段AB.BC的垂直平分线11.l2相交于点O，若∠1＝39°，则∠AOC＝　78°　．‎ ‎【分析】过O作射线BP，根据线段的垂直平分线的性质得AO＝OB＝OC和∠BDO＝∠BEO＝90°，根据四边形的内角和为360°得∠DOE+∠ABC＝180°，根据外角的性质得∠AOP＝∠A+∠ABO，∠COP＝∠C+∠OBC，相加可得结论．‎ ‎【解答】解：过O作射线BP，‎ ‎∵线段AB.BC的垂直平分线11.l2相交于点O，‎ ‎∴AO＝OB＝OC，∠BDO＝∠BEO＝90°，‎ ‎∴∠DOE+∠ABC＝180°，‎ ‎∵∠DOE+∠1＝180°，‎ ‎∴∠ABC＝∠1＝39°，‎ ‎∵OA＝OB＝OC，‎ ‎∴∠A＝∠ABO，∠OBC＝∠C，‎ ‎∵∠AOP＝∠A+∠ABO，∠COP＝∠C+∠OBC，‎ ‎∴∠AOC＝∠AOP+∠COP＝∠A+∠ABC+∠C＝2×39°＝78°，‎ 故答案为：78°．‎ ‎【点评】本题主要考查线段的垂直平分线的性质，等腰三角形的性质，三角形外角的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．‎ ‎7（2020•黑龙江省齐齐哈尔市•3分）等腰三角形的两条边长分别为3和4，则这个等腰三角形的周长是　10或11　．‎ ‎【分析】分3是腰长与底边长两种情况讨论求解即可．‎ ‎【解答】解：①3是腰长时，三角形的三边分别为3.3.4，‎ ‎∵此时能组成三角形，‎ ‎∴周长＝3+3+4＝10；‎ ‎②3是底边长时，三角形的三边分别为3.4.4，‎ 此时能组成三角形，‎ 所以周长＝3+4+4＝11．‎ 综上所述，这个等腰三角形的周长是10或11．‎ 故答案为：10或11．‎ ‎【点评】本题考查了等腰三角形的性质，难点在于要分情况讨论．‎ ‎8.（2020•湖北省黄冈市•3分）已知：如图，在△ABC中，点D在边BC上，AB＝AD＝DC，∠C＝35°，则∠BAD＝　40　度．‎ ‎【分析】根据等腰三角形的性质和三角形的内角和定理即可得到结论．‎ ‎【解答】解：∵AD＝DC，‎ ‎∴∠DAC＝∠C＝35°，‎ ‎∴∠ADB＝∠DAC+∠C＝70°．‎ ‎∵AB＝AD，‎ ‎∴∠B＝∠ADB＝70°，‎ ‎∴∠BAD＝180°﹣∠B﹣∠ADB＝180°﹣70°﹣70°＝40°．‎ 故答案为：40．．‎ ‎【点评】本题考查了等腰三角形的性质及三角形内角和为180°等知识．此类已知三角形边之间的关系求角的度数的题，一般是利用等腰（等边）三角形的性质得出有关角的度数，进而求出所求角的度数．‎ ‎9. （2020•江苏省苏州市•3分）如图，已知是一个锐角，以点为圆心，任意长为半径画弧，分别交、于点、，再分别以点、为圆心，大于长为半径画弧，两弧交于点，画射线．过点作，交射线于点，过点作，交于点．设，，则________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 连接AB交OD于点H，过点A作AG⊥ON于点G，根据等腰三角形的性质得OH⊥AB，AH=BH，从而得四边形ABED是平行四边形，利用勾股定理和三角形的面积法，求得AG的值，进而即可求解．‎ ‎【详解】连接AB交OD于点H，过点A作AG⊥ON于点G，‎ 由尺规作图步骤，可得：OD是∠MON的平分线，OA=OB，‎ ‎∴OH⊥AB，AH=BH，‎ ‎∵，‎ ‎∴DE∥AB，‎ ‎∵，‎ ‎∴四边形ABED是平行四边形，‎ ‎∴AB=DE=12，‎ ‎∴AH=6，‎ ‎∴OH=，‎ ‎∵OB∙AG=AB∙OH，‎ ‎∴AG===，‎ ‎∴=．‎ 故答案是：．‎ ‎【点睛】本题主要考查等腰三角形的性质，平行四边形的判定和性质定理，勾股定理，锐角三角函数的定义，添加合适的辅助线，构造直角三角形是解题的关键．‎ ‎ ‎ ‎10..（2020•贵州省安顺市•4分）如图，△ABC中，点E在边AC上，EB＝EA，∠A＝2∠CBE，CD垂直于BE的延长线于点D，BD＝8，AC＝11，则边BC的长为　　．‎ ‎【分析】延长BD到F，使得DF＝BD，根据等腰三角形的性质与判定，勾股定理即可求出答案．‎ ‎【解答】解：延长BD到F，使得DF＝BD，‎ ‎∵CD⊥BF，‎ ‎∴△BCF是等腰三角形，‎ ‎∴BC＝CF，‎ 过点C点作CH∥AB，交BF于点H ‎∴∠ABD＝∠CHD＝2∠CBD＝2∠F，‎ ‎∴HF＝HC，‎ ‎∵BD＝8，AC＝11，‎ ‎∴DH＝BH﹣BD＝AC﹣BD＝3，‎ ‎∴HF＝HC＝8﹣3＝5，‎ 在Rt△CDH，‎ ‎∴由勾股定理可知：CD＝4，‎ 在Rt△BCD中，‎ ‎∴BC＝＝4，‎ 故答案为：4‎ ‎【点评】本题考查勾股定理，解题的关键是熟练运用等腰三角形的性质与判定，本题属于中等题型．‎ 三.解答题 ‎1. （2020•江苏省淮安市•8分）如图，三条笔直公路两两相交，交点分别为A.B.C，测得∠CAB＝30°，∠ABC＝45°，AC＝8千米，求A.B两点间的距离．（参考数据：≈1.4，‎ ‎≈1.7，结果精确到1千米）．‎ ‎【分析】过点C作CD⊥AB于点D，在Rt△ACD中，通过解直角三角形可求出AD，CD的长，在Rt△BCD中，由∠BDC＝90°，∠CBD＝45°可得出BD＝CD，再结合AB＝AD+BD即可求出A.B两点间的距离．‎ ‎【解答】解：过点C作CD⊥AB于点D，如图所示．‎ 在Rt△ACD中，AC＝8千米，∠CAD＝30°，∠CAD＝90°，‎ ‎∴CD＝AC•sin∠CAD＝4千米，AD＝AC•cos∠CAD＝4千米≈6.8千米．‎ 在Rt△BCD中，CD＝4千米，∠BDC＝90°，∠CBD＝45°，‎ ‎∴∠BCD＝45°，‎ ‎∴BD＝CD＝4千米，‎ ‎∴AB＝AD+BD＝6.8+4≈11千米．‎ 答：A.B两点间的距离约为11千米．‎ ‎【点评】本题考查了解直角三角形以及等腰直角三角形，通过解直角三角形以及利用等腰直角三角形的性质，找出AD，BD的长是解题的关键．‎ ‎2.（2020•黑龙江省哈尔滨市•8分）已知：在△ABC中，AB＝AC，点D.点E在边BC上，BD＝CE，连接AD.AE．‎ ‎（1）如图1，求证：AD＝AE；‎ ‎（2）如图2，当∠DAE＝∠C＝45°时，过点B作BF∥AC交AD的延长线于点F，在不添加任何辅助线的情况下，请直接写出图2中的四个等腰三角形，使写出的每个等腰三角形的顶角都等于45°．‎ ‎【分析】（1）根据SAS可证△ABD≌△ACE，根据全等三角形的性质即可求解；‎ ‎（2）根据等腰三角形的判定即可求解．‎ ‎【解答】（1）证明：∵AB＝AC，‎ ‎∵∠B＝∠C，‎ 在△ABD和△ACE中，‎ ‎，‎ ‎∴△ABD≌△ACE（SAS），‎ ‎∴AD＝AE；‎ ‎（2）∵AD＝AE，‎ ‎∴∠ADE＝∠AED，‎ ‎∵BF∥AC，‎ ‎∴∠FDB＝∠C＝45°，‎ ‎∵∠ABC＝∠C＝∠DAE＝45°，∠BDF＝∠ADE，‎ ‎∴∠F＝∠BDF，∠BEA＝∠BAE，∠CDA＝∠CAD，‎ ‎∴满足条件的等腰三角形有：△ABE，△ACD，△DAE，△DBF．‎ ‎【点评】考查了全等三角形的判定与性质，等腰三角形的判定与性质，关键是熟练掌握它们的性质与定理．‎ ‎3. （2020•江苏省南京市•8分）如图，在△ABC中，AC＝BC，D是AB上一点，⊙O经过点A.C.D，交BC于点E，过点D作DF∥BC，交⊙O于点F．‎ 求证：（1）四边形DBCF是平行四边形；‎ ‎（2）AF＝EF．‎ ‎【分析】（1）根据等腰三角形的性质得出∠BAC＝∠B，根据平行线的性质得出∠ADF＝∠B，求出∠ADF＝∠CFD，根据平行线的判定得出BD∥CF，根据平行四边形的判定得出即可；‎ ‎（2）求出∠AEF＝∠B，根据圆内接四边形的性质得出∠ECF+∠EAF＝180°，根据平行线的性质得出∠ECF+∠B＝180°，求出∠AEF＝∠EAF，根据等腰三角形的判定得出即可．‎ ‎【解答】证明：（1）∵AC＝BC，‎ ‎∴∠BAC＝∠B，‎ ‎∵DF∥BC，‎ ‎∴∠ADF＝∠B，‎ ‎∵∠BAC＝∠CFD，‎ ‎∴∠ADF＝∠CFD，‎ ‎∴BD∥CF，‎ ‎∵DF∥BC，‎ ‎∴四边形DBCF是平行四边形；‎ ‎（2）连接AE，‎ ‎∵∠ADF＝∠B，∠ADF＝∠AEF，‎ ‎∴∠AEF＝∠B，‎ ‎∵四边形AECF是⊙O的内接四边形，‎ ‎∴∠ECF+∠EAF＝180°，‎ ‎∵BD∥CF，‎ ‎∴∠ECF+∠B＝180°，‎ ‎∴∠EAF＝∠B，‎ ‎∴∠AEF＝∠EAF，‎ ‎∴AE＝EF．‎ ‎【点评】本题考查了平行线的性质和判定，平行四边形的判定，圆内接四边形，等腰三角形的判定等知识点，能综合运用知识点进行推理是解此题的关键．‎ ‎4.（2020•河南省•11分）将正方形ABCD的边AB绕点A逆时针旋转至AB′，记旋转角为α，连接BB′，过点D作DE垂直于直线BB′，垂足为点E，连接DB′，CE．‎ ‎（1）如图1，当α＝60°时，△DEB′的形状为　等腰直角三角形　，连接BD，可求出的值为　　；‎ ‎（2）当0°＜α＜360°且α≠90°时，‎ ‎①（1）中的两个结论是否仍然成立？如果成立，请仅就图2的情形进行证明；如果不成立，请说明理由；‎ ‎②当以点B′，E，C，D为顶点的四边形是平行四边形时，请直接写出的值．‎ ‎【分析】（1）由旋转的性质得出AB＝AB'，∠BAB'＝60°，证得△ABB'是等边三角形，可得出△DEB'是等腰直角三角形．证明△BDB'∽△CDE，得出．‎ ‎（2）①得出∠EDB'＝∠EB'D＝45°，则△DEB'是等腰直角三角形，得出，证明△B'DB∽△EDC，由相似三角形的性质可得出．‎ ‎②分两种情况画出图形，由平行四边形的性质可得出答案．‎ ‎【解答】解：（1）∵AB绕点A逆时针旋转至AB′，‎ ‎∴AB＝AB'，∠BAB'＝60°，‎ ‎∴△ABB'是等边三角形，‎ ‎∴∠BB'A＝60°，‎ ‎∴∠DAB'＝∠BAD﹣∠BAB'＝90°﹣60°＝30°，‎ ‎∵AB'＝AB＝AD，‎ ‎∴∠AB'D＝∠ADB'，‎ ‎∴∠AB'D＝＝75°，‎ ‎∴∠DB'E＝180°﹣60°﹣75°＝45°，‎ ‎∵DE⊥B'E，‎ ‎∴∠B'DE＝90°﹣45°＝45°，‎ ‎∴△DEB'是等腰直角三角形．‎ ‎∵四边形ABCD是正方形，‎ ‎∴∠BDC＝45°，‎ ‎∴，‎ 同理，‎ ‎∴，‎ ‎∵∠BDB'+∠B'DC＝45°，∠EDC+∠B'DC＝45°，‎ ‎∴BDB'＝∠EDC，‎ ‎∴△BDB'∽△CDE，‎ ‎∴．‎ 故答案为：等腰直角三角形，．‎ ‎（2）①两结论仍然成立．‎ 证明：连接BD，‎ ‎∵AB＝AB'，∠BAB'＝α，‎ ‎∴∠AB'B＝90°﹣，‎ ‎∵∠B'AD＝α﹣90°，AD＝AB'，‎ ‎∴∠AB'D＝135°﹣，‎ ‎∴∠EB'D＝∠AB'D﹣∠AB'B＝135°﹣＝45°，‎ ‎∵DE⊥BB'，‎ ‎∴∠EDB'＝∠EB'D＝45°，‎ ‎∴△DEB'是等腰直角三角形，‎ ‎∴，‎ ‎∵四边形ABCD是正方形，‎ ‎∴，∠BDC＝45°，‎ ‎∴，‎ ‎∵∠EDB'＝∠BDC，‎ ‎∴∠EDB'+∠EDB＝∠BDC+∠EDB，‎ 即∠B'DB＝∠EDC，‎ ‎∴△B'DB∽△EDC，‎ ‎∴．‎ ‎②＝3或1．‎ 若CD为平行四边形的对角线，‎ 点B'在以A为圆心，AB为半径的圆上，取CD的中点．连接BO交⊙A于点B'，‎ 过点D作DE⊥BB'交BB'的延长线于点E，‎ 由（1）可知△B'ED是等腰直角三角形，‎ ‎∴B'D＝B'E，‎ 由（2）①可知△BDB'∽△CDE，且BB'＝CE．‎ ‎∴＝+1＝+1＝+1＝+1＝3．‎ 若CD为平行四边形的一边，如图3，‎ 点E与点A重合，‎ ‎∴＝1．‎ 综合以上可得＝3或1．‎ ‎【点评】本题是四边形综合题，考查了正方形的性质，等腰直角三角形的判定与性质，旋转的性质，等边三角形的判定与性质，相似三角形的判定与性质等知识，熟练掌握相似三角形的判定与性质是解题的关键．‎ ‎5.（2020•河北省•12分）如图1和图2，在△ABC中，AB＝AC，BC＝8，tanC＝．点K在AC边上，点M，N分别在AB，BC上，且AM＝CN＝2．点P从点M出发沿折线MB﹣BN匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ＝∠B．‎ ‎（1）当点P在BC上时，求点P与点A的最短距离；‎ ‎（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长；‎ ‎（3）设点P移动的路程为x，当0≤x≤3及3≤x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；‎ ‎（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK＝，请直接写出点K被扫描到的总时长．‎ ‎【分析】（1）如图1中，过点A作AH⊥BC于H．解直角三角形求出AH即可．‎ ‎（2）利用相似三角形的性质求解即可．‎ ‎（3）分两种情形：当0≤x≤3时，当3＜x≤9时，分别画出图形求解即可．‎ ‎（4）求出CK的长度，以及CQ的最大值，利用路程与速度的关系求解即可．‎ ‎【解答】解：（1）如图1中，过点A作AH⊥BC于H．‎ ‎∵AB＝AC，AH⊥BC，‎ ‎∴BH＝CH＝4，∠B＝∠C，‎ ‎∴tan∠B＝tan∠C＝＝，‎ ‎∴AH＝3，AB＝AC＝＝＝5．‎ ‎∴当点P在BC上时，点P到A的最短距离为3．‎ ‎（2）如图1中，∵∠APQ＝∠B，‎ ‎∴PQ∥BC，‎ ‎∴△APQ∽△ABC，‎ ‎∵PQ将△ABC的面积分成上下4：5，‎ ‎∴＝（）2＝，‎ ‎∴＝，‎ ‎∴AP＝，‎ ‎∴PM＝AP＝AM＝﹣2＝．‎ ‎（3）当0≤x≤3时，如图1﹣1中，过点P作PJ⊥CA交CA的延长线于J．‎ ‎∵PQ∥BC，‎ ‎∴＝，∠AQP＝∠C，‎ ‎∴＝，‎ ‎∴PQ＝（x+2），‎ ‎∵sin∠AQP＝sin∠C＝，‎ ‎∴PJ＝PQ•sin∠AQP＝（x+2）．‎ 当3≤x≤9时，如图2中，过点P作PJ⊥AC于J．‎ 同法可得PJ＝PC•sin∠C＝（11﹣x）．‎ ‎（4）由题意点P的运动速度＝＝单位长度/秒．‎ 当3＜x≤9时，设CQ＝y．‎ ‎∵∠APC＝∠B+∠BAP＝∠APQ+∠CPQ，∠APQ＝∠B，‎ ‎∴∠BAP＝∠CPQ，‎ ‎∵∠B＝∠C，‎ ‎∴△ABP∽△PCQ，‎ ‎∴＝，‎ ‎∴＝，‎ ‎∴y＝﹣（x﹣7）2+，‎ ‎∵﹣＜0，‎ ‎∴x＝7时，y有最大值，最大值＝，‎ ‎∵AK＝，‎ ‎∴CK＝5﹣＝＜‎ 当y＝时，＝﹣（x﹣7）2+，‎ 解得x＝7±，‎ ‎∴点K被扫描到的总时长＝（+6﹣3）÷＝23秒．‎ 方法二：①点P在AB上的时候，有11/4个单位长度都能扫描到点K；‎ ‎②在BN阶段，当x在3～5.5（即7﹣1.5）的过程，是能扫到K点的，在5.5～8.5（即7+1.5）的过程是扫不到点K的，但在8.5～9（即点M到N全部的路程）能扫到点K ‎．所以扫到的时间是[（9﹣8.5）+（5.5﹣3）+]÷＝23（秒）．‎ ‎【点评】本题属于三角形综合题，考查了等腰三角形的性质，解直角三角形，相似三角形的判定和性质，二次函数的性质等知识，解题的关键是理解题意，学会构建二次函数解决CQ的最值问题，属于中考压轴题．‎ ‎6（2020•广东省•6分）如题20图，在△ABC中，点D.E分别是AB.AC边上的点，BD=CE，∠ABE=∠ACD，BE与CD相交于点F．求证：△ABC是等腰三角形．‎ ‎【答案】‎ 证明：‎ ‎∵BD=CE，∠ABE=∠ACD，∠DFB=∠CFE ‎∴△BFDF≌△CFE（AAS）‎ ‎∴∠DBF=∠ECF ‎∵∠DBF+∠ABE=∠ECF+∠ACD ‎∴∠ABC=∠ACB ‎∴AB=AC ‎∴△ABC是等腰三角形 ‎【解析】等式的性质、等角对等边 ‎【考点】全等三角形的判定方法、等腰三角形的判定方法 www.czsx.com.cn ‎7.（2020•贵州省安顺市•10分）如图，AB为⊙O的直径，四边形ABCD内接于⊙O，对角线AC，BD交于点E，⊙O的切线AF交BD的延长线于点F，切点为A，且∠CAD＝∠ABD．‎ ‎（1）求证：AD＝CD；‎ ‎（2）若AB＝4，BF＝5，求sin∠BDC的值．‎ ‎【分析】（1）根据圆周角定理得∠ABD＝∠ACD，进而得∠ACD＝∠CAD ‎，便可由等腰三角形判定定理得AD＝CD；‎ ‎（2）证明△ADF≌△ADE，得AE＝AF，DE＝DF，由勾股定理求得AF，由三角形面积公式求得AD，进而求得DE，BE，再证明△BEC∽△AED，得BC，进而求得sin∠BAC便可．‎ ‎【解答】解：（1）证明：∵∠CAD＝∠ABD，‎ 又∵∠ABD＝∠ACD，‎ ‎∴∠ACD＝∠CAD，‎ ‎∴AD＝CD；‎ ‎（2）∵AF是⊙O的切线，‎ ‎∴∠FAB＝90°，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ACB＝∠ADB＝∠ADF＝90°，‎ ‎∴∠ABD+∠BAD＝∠BAD+∠FAD＝90°，‎ ‎∴∠ABD＝∠FAD，‎ ‎∵∠ABD＝∠CAD，‎ ‎∴∠FAD＝∠EAD，‎ ‎∵AD＝AD，‎ ‎∴△ADF≌△ADE（ASA），‎ ‎∴AF＝AE，DF＝DE，‎ ‎∵AB＝4，BF＝5，‎ ‎∴AF＝，‎ ‎∴AE＝AF＝3，‎ ‎∵，‎ ‎∴，‎ ‎∴DE＝，‎ ‎∴BE＝BF﹣2DE＝，‎ ‎∵∠AED＝∠BEC，∠ADE＝∠BCE＝90°，‎ ‎∴△BEC∽△AED，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ ‎∵∠BDC＝∠BAC，‎ ‎∴．‎ ‎【点评】本题主要考查了圆的切线的性质，圆周角定理，相似三角形的性质与判定，全等三角形的性质与判定，等腰三角形的性质与判定，解直角三角形的应用，勾股定理，关键是证明三角形全等与相似．‎ ‎ ‎ ‎ ‎