2006年四川省高考数学试卷(理科)【附答案、word版本,可再编辑;B4纸型两栏】
2006年四川省高考数学试卷(理科)
一、选择题(共12小题,每小题5分,满分60分)
1. 已知集合A={x|x2-5x+6≤0},B={x||2x-1|>3},则集合A∩B=( )
A.{x|2≤x≤3} B.{x|2≤x<3} C.{x|2
0),f(x)的导函数是f'(x).对任意两个不相等的正数x1、x2,证明:
(1)当a≤0时,f(x1)+f(x2)2>f(x1+x22);
(2)当a≤4时,|f'(x1)-f'(x2)|>|x1-x2|.
9 / 9
参考答案与试题解析
2006年四川省高考数学试卷(理科)
一、选择题(共12小题,每小题5分,满分60分)
1.C
2.D
3.D
4.B
5.D
6.B
7.A
8.C
9.A
10.C
11.A
12.B
二、填空题(共4小题,每小题4分,满分16分)
13.arctan2
14.110
15.35
16.①③
三、解答题(共6小题,满分74分)
17.(1)∵ m→⋅n→=1
∴ (-1,3)⋅(cosA,sinA)=1
即3sinA-cosA=2(sinA⋅32-cosA⋅12)=1,sin(A-π6)=12
∵ 0=|HP→|⋅|HF→|˙=221
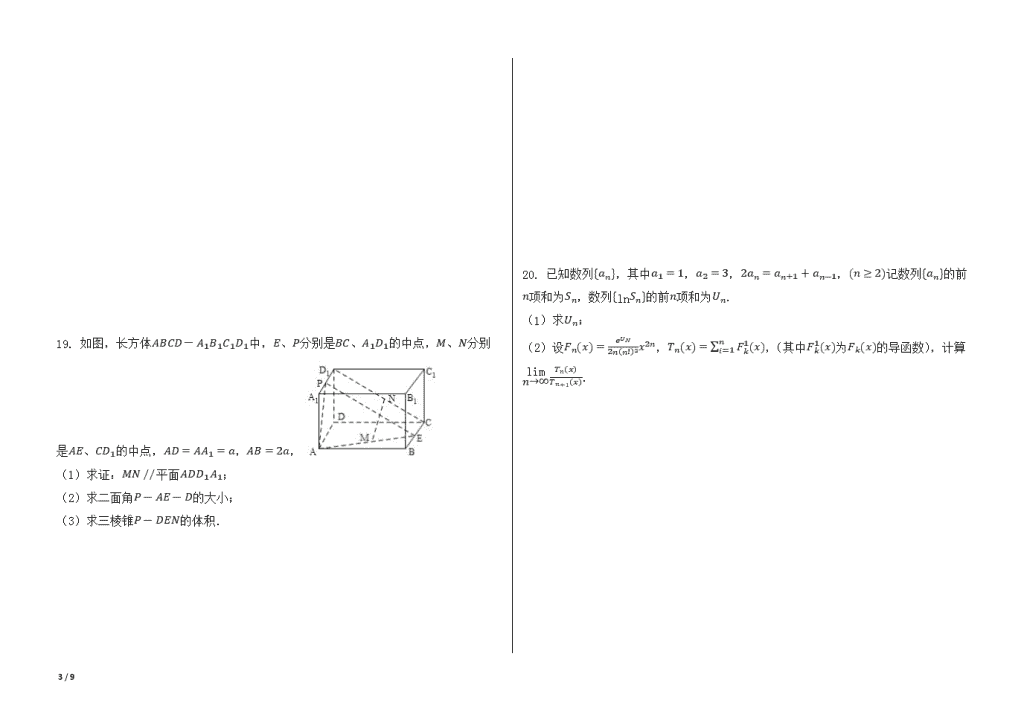
故:二面角P-AE-D的大小为arccos22121
(3)设n1→=(x1,y1,z1)为平面DEN的法向量,
则n1→⊥DE→,n1→⊥DN→
又DE→=(a2,2a,0),DN→=(0,a,a2),DP→=(a2,0,a)
∴ a2x1+2ay1=02y1+a2z1=0即x1=-4y1z1=-2y1∴ 可取n1→=(4,-1,2)
∴ P点到平面DEN的距离为d=|n1→|˙=|2a+2a|16+1+4=4a21
∵ cos⟨DE→,DN→>=|DE→|⋅|DN→|˙=885,sin⟨DE→,DN→>=2185
∴ S△DEN=12|DE→|⋅|DN→|⋅sin⟨DE→,DN→>=218a2
∴ VP-DEN=13S△DEN⋅d=13×218a2×4a21=a36
20.解:(1)由题意,{an}是首项为1,公差为2的等差数列
前n项和Sn=1+1+2(n-1)2⋅n=n2,
lnSn=lnn2=2lnnUn=2(ln1+ln2+...+lnn)=2ln(n!)
(2)Fn(x)=eUn2n(n!)2⋅x2n=(n!)22n(n!)2⋅x2n=x2n2nFn'(x)=x2n-1Tn(x)=k=1nFk'(x)=k=1nx2k-1=x(1-x2n)1-x2(01)
limn→∞Tn(x)Tn+1(x)=limn→∞1-x2n1-x2n+2=1(01)
21.解:由双曲线的定义可知,
曲线E是以F1(-2,0),F2(2,0)为焦点的双曲线的左支,
且c=2,a=1,易知b=1
故曲线E的方程为x2-y2=1(x<0)
设A(x1, y1),B(x2, y2),由题意建立方程组y=kx-1x2-y2=1
消去y,得(1-k2)x2+2kx-2=0
又已知直线与双曲线左支交于两点A,B,
有1-k2≠0△=(2k)2+8(1-k2)>0x1+x2=-2k1-k2<0x1x2=-21-k2>0
9 / 9
解得-214[(x12+x22)+2x1x2]2=(x1+x22)2①
又(x1+x2)2=(x12+x22)+2x1x2>4x1x2
∴ x1+x2x1x2>4x1+x2②
∵ x1x2<x1+x22
∴ lnx1x2(x1+x22)2+4x1+x2+alnx1x2,
即f(x1)+f(x2)2>f(x1+x22).
(2)证法一:由f(x)=x2+2x+alnx,得f'(x)=2x-2x2+ax
∴ |f'(x1)-f'(x2)|=|(2x1-2x12+ax1)-(2x2-2x22+ax2)|=|x1-x2|⋅|2+2(x1+x2)x12x22-ax1x2||f'(x1)-f'(x2)|>|x1-x2|⇔|2+2(x1+x2)x12x22-ax1x2|>1
下面证明对任意两个不相等的正数x1,x2,有2+2(x1+x2)x12x22-ax1x2>1恒成立
9 / 9
即证ax1x2+4x1x2
设t=x1x2,u(x)=t2+4t(t>0),
则u'(x)=2t-4t2,
令u'(x)=0得t=32,列表如下:
t
(0,32)
32
(32,+∞)
u'(t)
-
0
+
u(t)
□
极小值334
□
u(t)≥334=3108>4≥a
∴ x1x2+2(x1+x2)x1x2>a
∴ 对任意两个不相等的正数x1,x2,恒有|f'(x1)-f'(x2)|>|x1-x2|
证法二:由f(x)=x2+2x+alnx,
得f'(x)=2x-2x2+ax
∴ |f'(x1)-f'(x2)|=|(2x1-2x12+ax1)-(2x2-2x22+ax2)|=|x1-x2|⋅|2+2(x1+x2)x12x22-ax1x2|
∵ x1,x2是两个不相等的正数
∴ 2+2(x1+x2)x12x22-ax1x2>2+4(x1x2)3-ax1x2≥2+4(x1x2)3-4x1x2
设t=1x1x2,u(t)=2+4t3-4t2(t>0)
则u'(t)=4t(3t-2),列表:
t
(0,23)
23
(23,+∞)
u'(t)
-
0
+
u(t)
□
极小值3827
□
∴ u=3827>1即2+2(x1+x2)x12x22-ax1x2>1
∴ |f'(x1)-f'(x2)|=|x1-x2|⋅|2+2(x1+x2)x12x22-ax1x2|>|x1-x2|
即对任意两个不相等的正数x1,x2,恒有|f'(x1)-f'(x2)|>|x1-x2|
9 / 9