- 2021-04-13 发布 |
- 37.5 KB |
- 48页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届高考数学一轮复习第二章函数概念及基本初等函数Ⅰ第7节函数的图象课件新人教A版
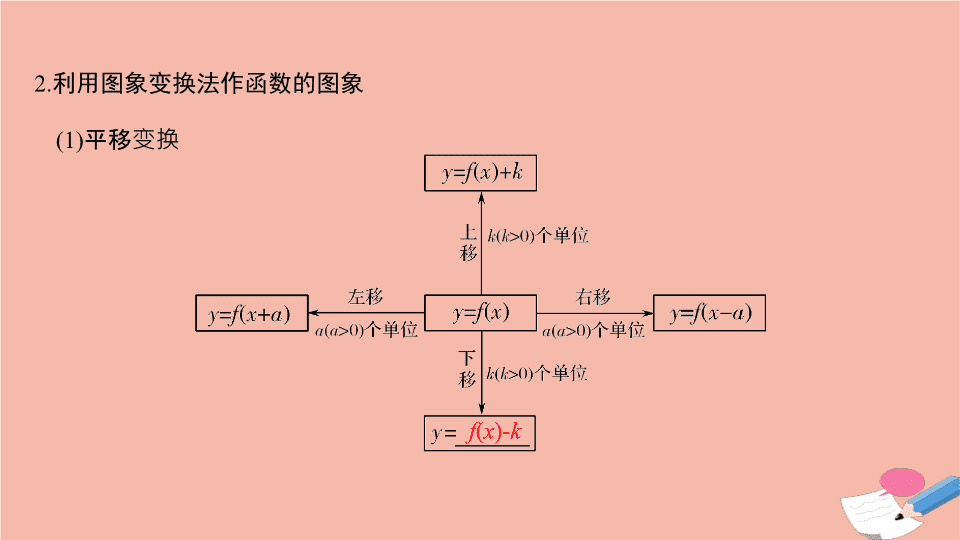
第 7 节 函数的图象 考试要求 1. 在实际情境中,会根据不同的需要选择恰当的方法 ( 如图象法、列表法、解析法 ) 表示函数; 2. 会运用基本初等函数的图象分析函数的性质,解决方程解的个数与不等式解的问题 . 知 识 梳 理 1. 利用描点法作函数的图象 步骤: (1) 确定函数的定义域; (2) 化简函数解析式; (3) 讨论函数的性质 ( 奇偶性、单调性、周期性、对称性等 ) ; (4) 列表 ( 尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等 ) ,描点,连线 . 2. 利用图象变换法作函数的图象 (1) 平移变换 f ( x )- k - f ( x ) f ( - x ) - f ( - x ) log a x | f ( x )| f (| x |) [ 常用结论与微点提醒 ] 1. 记住几个重要结论 (1) 函数 y = f ( x ) 与 y = f (2 a - x ) 的图象关于直线 x = a 对称 . (2) 函数 y = f ( x ) 与 y = 2 b - f (2 a - x ) 的图象关于点 ( a , b ) 中心对称 . (3) 若函数 y = f ( x ) 对定义域内任意自变量 x 满足: f ( a + x ) = f ( a - x ) ,则函数 y = f ( x ) 的图象关于直线 x = a 对称 . 2. 图象的左右平移仅仅是相对于 x 而言,如果 x 的系数不是 1 ,常需把系数提出来,再进行变换 . 3. 图象的上下平移仅仅是相对于 y 而言的,利用 “ 上减下加 ” 进行 . 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) (1) 当 x ∈ (0 ,+ ∞ ) 时,函数 y = | f ( x )| 与 y = f (| x |) 的图象相同 .( ) (2) 函数 y = af ( x ) 与 y = f ( ax )( a >0 且 a ≠ 1) 的图象相同 .( ) (3) 函数 y = f ( x ) 与 y =- f ( x ) 的图象关于原点对称 .( ) (4) 若函数 y = f ( x ) 满足 f (1 + x ) = f (1 - x ) ,则函数 f ( x ) 的图象关于直线 x = 1 对称 .( ) 解析 (1) 令 f ( x ) =- x ,当 x ∈ (0 ,+ ∞ ) 时, y = | f ( x )| = x , y = f (| x |) =- x ,两者图象不同, (1) 错 . (2) 中两函数当 a ≠ 1 时, y = af ( x ) 与 y = f ( ax ) 是由 y = f ( x ) 分别进行振幅与周期变换得到,两图象不同, (2) 错 . (3) y = f ( x ) 与 y =- f ( x ) 图象关于 x 轴对称, (3) 错 . (4) 中, f (2 - x ) = f [1 + (1 - x )] = f [1 - (1 - x )] = f ( x ) ,所以 y = f ( x ) 的图象关于直线 x = 1 对称, (4) 正确 . 答案 (1) × (2) × (3) × (4) √ 解析 其图象是由 y = x 2 图象中 x <0 的部分和 y = x - 1 图象中 x ≥ 0 的部分组成 . 答案 C 3. ( 新教材必修第一册 P140 习题 4.4T6) 在 2 h 内将某种药物注射进患者的血液中,在注射期间,血液中的药物含量呈线性增加;停止注射后,血液中的药物含量呈指数衰减,能反映血液中药物含量 Q 随时间 t 变化的图象是 ( ) 解析 依题意,在 2 h 内血液中药物含量 Q 持续增加,停止注射后, Q 呈指数衰减,图象 B 适合 . 答案 B 4. ( 一题多解 )(2018· 全国 Ⅲ 卷 ) 下列函数中,其图象与函数 y = ln x 的图象关于直线 x = 1 对称的是 ( ) A. y = ln(1 - x ) B. y = ln(2 - x ) C. y = ln(1 + x ) D. y = ln(2 + x ) 解析 法一 设所求函数图象上任一点的坐标为 ( x , y ) ,则其关于直线 x = 1 的对称点的坐标为 (2 - x , y ) ,由对称性知点 (2 - x , y ) 在函数 f ( x ) = ln x 的图象上,所以 y = ln(2 - x ). 法二 由题意知,对称轴上的点 (1 , 0) 在函数 y = ln x 的图象上也在所求函数的图象上,代入选项中的函数表达式逐一检验,排除 A , C , D ,选 B. 答案 B ∴ f ( x ) 为奇函数,排除 A. 答案 D 答案 (2 , 8] 考点一 作函数的图象 【例 1 】 作出下列函数的图象: (2) 将函数 y = log 2 x 的图象向左平移一个单位,再将 x 轴下方的部分沿 x 轴翻折上去,即可得到函数 y = |log 2 ( x + 1)| 的图象,如图 ② . 规律方法 作函数图象的一般方法 (1) 直接法 . 当函数解析式 ( 或变形后的解析式 ) 是熟悉的基本函数时,就可根据这些函数的特征描出图象的关键点直接作出 . (2) 图象变换法 . 若函数图象可由某个基本函数的图象经过平移、翻折、对称得到,可利用图象变换作出,并应注意平移变换与伸缩变换的顺序对变换单位及解析式的影响 . 【训练 1 】 分别作出下列函数的图象: (1) y = |lg x | ; (2) y = sin | x |. 解 (1) 先作出函数 y = lg x 的图象,再将 x 轴下方的部分沿 x 轴翻折上去,即可得函数 y = |lg x | 的图象,如图 ① 实线部分 . (2) 当 x ≥ 0 时, y = sin| x | 与 y = sin x 的图象完全相同,又 y = sin| x | 为偶函数,图象关于 y 轴对称,其图象如图 ② . 考点二 函数图象的辨识 所以 f ( x ) 是奇函数,排除选项 C. 所以 f ( x ) 的定义域为 ( - 1 , 0) ∪ (0 , 1) ,关于原点对称 . 又 f ( x ) = f ( - x ) ,所以函数 f ( x ) 是偶函数,图象关于 y 轴对称,排除 A ; 当 0< x <1 时, lg | x |<0 , f ( x )<0 ,排除 C ; 当 x >0 且 x → 0 时, f ( x ) → 0 ,排除 D ,只有 B 项符合 . 答案 (1)B (2)B 规律方法 1. 抓住函数的性质,定性分析: (1) 从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置; (2) 从函数的单调性,判断图象的变化趋势; (3) 从周期性,判断图象的循环往复; (4) 从函数的奇偶性,判断图象的对称性 . 2. 抓住函数的特征,定量计算: 从函数的特征点,利用特征点、特殊值的计算分析解决问题 . 法二 当 x = 1 时, f (1) = 1 + 1 + sin 1 = 2 + sin 1>2 ,排除 A , C ;又当 x → + ∞ 时, y → + ∞ ,排除 B ,而 D 满足 . 答案 (1)B (2)D 考点三 函数图象的应用 多维探究 角度 1 研究函数的性质 【例 3 - 1 】 已知函数 f ( x ) = x | x | - 2 x ,则下列结论正确的是 ( ) A. f ( x ) 是偶函数,递增区间是 (0 ,+ ∞ ) B. f ( x ) 是偶函数,递减区间是 ( - ∞ , 1) C. f ( x ) 是奇函数,递减区间是 ( - 1 , 1) D. f ( x ) 是奇函数,递增区间是 ( - ∞ , 0) 答案 C 角度 2 函数图象在不等式中的应用 【例 3 - 2 】 (1) (2020· 哈尔滨模拟 ) 已知函数 f ( x ) = 2 - | x | ,若关于 x 的不等式 f ( x ) ≥ x 2 - x - m 的解集中有且仅有 1 个整数,则实数 m 的取值范围为 ( ) A.[ - 3 ,- 1) B.( - 3 ,- 1) C.[ - 2 ,- 1) D.( - 2 ,- 1) 解析 (1) 在同一平面直角坐标系中作出函数 y = f ( x ) , y = x 2 - x - m 的图象如图所示 . 由图可知,不等式 f ( x ) ≥ x 2 - x - m 的解集中的整数解为 x = 0 , 角度 3 求参数的取值范围 【例 3 - 3 】 设函数 f ( x ) = | x 2 - 2 x | - ax - a ,其中 a >0 ,若只存在两个整数 x ,使得 f ( x )<0 ,则 a 的取值范围是 ______. 解析 f ( x ) = | x 2 - 2 x | - ax - a <0 ,则 | x 2 - 2 x |< ax + a , 分别画出 y = | x 2 - 2 x | 与 y = a ( x + 1) 的图象,如图所示 . ∵ 只存在两个整数 x ,使得 f ( x )<0 , 当 x = 1 时, |1 2 - 2| = 1 ,令 2 a = 1 , 规律方法 1. 利用函数的图象研究函数的性质 对于已知或易画出其在给定区间上图象的函数,其性质 ( 单调性、奇偶性、周期性、最值 ( 值域 ) 、零点 ) 常借助于图象研究,但一定要注意性质与图象特征的对应关系 . 2. 利用函数的图象可解决某些方程和不等式的求解问题,方程 f ( x ) = g ( x ) 的根就是函数 f ( x ) 与 g ( x ) 图象交点的横坐标;不等式 f ( x )< g ( x ) 的解集是函数 f ( x ) 的图象位于 g ( x ) 图象下方的点的横坐标的集合,体现了数形结合思想 . A. 函数 f ( x ) 的图象关于点 (1 , 0) 中心对称 B. 函数 f ( x ) 在 ( - ∞ , 1) 上是增函数 C. 函数 f ( x ) 的图象关于直线 x = 1 对称 D. 函数 f ( x ) 的图象上至少存在两点 A , B ,使得直线 AB ∥ x 轴 (2) ( 角度 2) 已知函数 y = f ( x ) 的图象是如图所示的折线 ACB ,且函数 g ( x ) = log 2 ( x + 1) ,则不等式 f ( x ) ≥ g ( x ) 的解集是 ( ) A.{ x | - 1< x ≤ 0} B.{ x | - 1 ≤ x ≤ 1} C.{ x | - 1< x ≤ 1} D.{ x | - 1< x ≤ 2} (2) 令 g ( x ) = y = log 2 ( x + 1) ,作出函数 g ( x ) 的图象如图, ∴ 结合图象知不等式 f ( x ) ≥ log 2 ( x + 1) 的解集为 { x | - 1< x ≤ 1}. 答案 (1)A (2)C (3)B 直观想象 —— 函数图象的活用 直观想象是发现和提出问题,分析和解决问题的重要手段,在数学研究的探索中,通过直观手段的运用以及借助直观展开想象,从而发现问题、解决问题的例子比比皆是,并贯穿于数学研究过程的始终,而数形结合思想是典型的直观想象范例 . 类型 1 根据函数图象特征,确定函数解析式 函数解析式与函数图象是函数的两种重要表示法,图象形象直观,解析式易于研究函数性质,可根据需要,相互转化 . 【例 1 】 (2020· 长沙模拟 ) 如图,已知函数 f ( x ) 的图象关于坐标原点对称,则函数 f ( x ) 的解析式可能是 ( ) 答案 C 类型 2 利用函数的图象研究函数的性质 对于已知或易画出其在给定区间上图象的函数,其性质 ( 单调性、奇偶性、周期性、最值 ( 值域 ) 、零点 ) 常借助图象研究,但一定要注意性质与图象特征的对应关系 . 【例 2 】 已知 f ( x ) = 2 x - 1 , g ( x ) = 1 - x 2 ,规定:当 | f ( x )| ≥ g ( x ) 时, h ( x ) = | f ( x )| ;当 | f ( x )| < g ( x ) 时, h ( x ) =- g ( x ) ,则 h ( x )( ) A. 有最小值- 1 ,最大值 1 B. 有最大值 1 ,无最小值 C. 有最小值- 1 ,无最大值 D. 有最大值- 1 ,无最小值 解析 画出 y = | f ( x )| = |2 x - 1| 与 y = g ( x ) = 1 - x 2 的图象,它们交于 A , B 两点 . 由 “ 规定 ” ,在 A , B 两侧, | f ( x )| ≥ g ( x ) ,故 h ( x ) = | f ( x )| ;在 A , B 之间, | f ( x )|< g ( x ) ,故 h ( x ) =- g ( x ). 综上可知, y = h ( x ) 的图象是图中的实线部分,因此 h ( x ) 有最小值- 1 ,无最大值 . 答案 C A.5 B.6 C.7 D.8 答案 C 思维升华 求解图象交点横、纵坐标之和的问题,常利用图象的对称性求解,即找出两图象的公共对称轴或对称中心,从而得出各交点的公共对称轴或对称中心,由此得出定值求解 . 类型 3 利用函数的图象求解方程或不等式 若研究的方程 ( 不等式 ) 不能用代数法求解,但其与基本初等函数有关,常将方程 ( 不等式 ) 问题转化为两函数图象的交点或图象的上下位置关系,然后由图象的几何直观数形结合求解 . 解析 f ( x ) = 2sin x cos x - x 2 = sin 2 x - x 2 ,函数 f ( x ) 的零点个数可转化为函数 y 1 = sin 2 x 与 y 2 = x 2 图象的交点个数,在同一坐标系中画出 y 1 = sin 2 x 与 y 2 = x 2 的图象如图所示: 由图可知两函数图象有 2 个交点,则 f ( x ) 的零点个数为 2. 答案 2查看更多