2008年北京市高考数学试卷(理科)

2008年北京市高考数学试卷(理科)

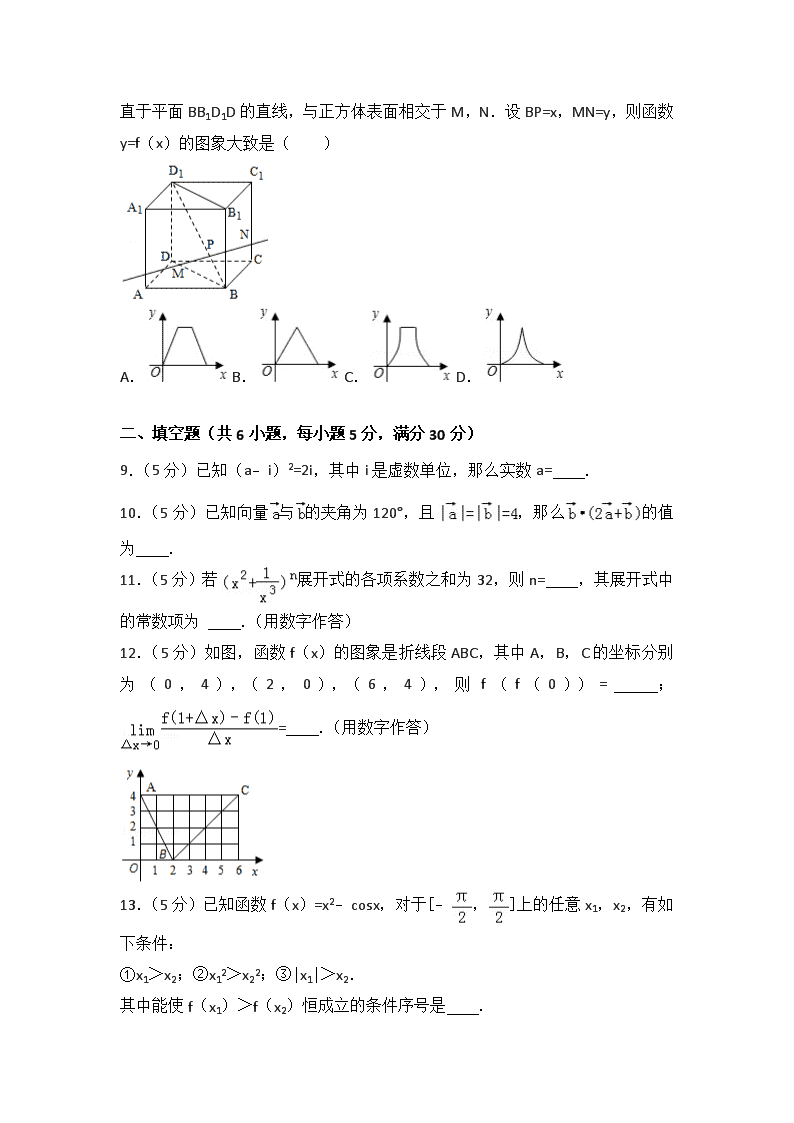
‎2008年北京市高考数学试卷（理科）‎ ‎　‎ 一、选择题（共8小题，每小题5分，满分40分）‎ ‎1．（5分）已知全集U=R，集合A={x|﹣2≤x＜3}，B={x|x＜﹣1或x≥4}，那么集合A∩B等于（　　）‎ A．{x|﹣1＜x＜3} B．{x|x≤﹣1或x＞3} C．{x|﹣2≤x＜﹣1} D．{x|﹣1≤x＜3}‎ ‎2．（5分）若a=20.5，b=logπ3，c=log2sin，则（　　）‎ A．a＞b＞c B．b＞a＞c C．c＞a＞b D．b＞c＞a ‎3．（5分）“函数f（x）（x∈R）存在反函数”是“函数f（x）在R上为增函数”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎4．（5分）若点P到直线x=﹣1的距离比它到点（2，0）的距离小1，则点P的轨迹为（　　）‎ A．圆 B．椭圆 C．双曲线 D．抛物线 ‎5．（5分）若实数x，y满足则z=3x+2y的最小值是（　　）‎ A．0 B．1 C． D．9‎ ‎6．（5分）已知数列{an}对任意的p，q∈N*满足ap+q=ap+aq，且a2=﹣6，那么a10等于（　　）‎ A．﹣165 B．﹣33 C．﹣30 D．﹣21‎ ‎7．（5分）过直线y=x上的一点作圆（x﹣5）2+（y﹣1）2=2的两条切线l1，l2，当直线l1，l2关于y=x对称时，它们之间的夹角为（　　）‎ A．30° B．45° C．60° D．90°‎ ‎8．（5分）如图，动点P在正方体ABCD﹣A1B1C1D1的对角线BD1‎ 上．过点P作垂直于平面BB1D1D的直线，与正方体表面相交于M，N．设BP=x，MN=y，则函数y=f（x）的图象大致是（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（共6小题，每小题5分，满分30分）‎ ‎9．（5分）已知（a﹣i）2=2i，其中i是虚数单位，那么实数a=　　．‎ ‎10．（5分）已知向量与的夹角为120°，且，那么的值为　　．‎ ‎11．（5分）若展开式的各项系数之和为32，则n=　　，其展开式中的常数项为 　　．（用数字作答）‎ ‎12．（5分）如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f（f（0））=　　；=　　．（用数字作答）‎ ‎13．（5分）已知函数f（x）=x2﹣cosx，对于[﹣，]上的任意x1，x2，有如下条件：‎ ‎①x1＞x2；②x12＞x22；③|x1|＞x2．‎ 其中能使f（x1）＞f（x2）恒成立的条件序号是　　．‎ ‎14．（5分）某校数学课外小组在坐标纸上，为学校的一块空地设计植树方案如下：第k棵树种植在点Pk（xk，yk）处，其中x1=1，y1=1，当k≥2时，T（a）表示非负实数a的整数部分，例如T（2.6）=2，T（0.2）=0．按此方案，第6棵树种植点的坐标应为　　；第2009棵树种植点的坐标应为　　．‎ ‎　‎ 三、解答题（共6小题，满分80分）‎ ‎15．（13分）已知函数f（x）=sin2ωx+sinωxsin（ωx+）（ω＞0）的最小正周期为π．‎ ‎（1）求ω的值；‎ ‎（2）求函数f（x）在区间[0，]上的取值范围．‎ ‎16．（14分）如图，在三棱锥P﹣ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC．‎ ‎（Ⅰ）求证：PC⊥AB；‎ ‎（Ⅱ）求二面角B﹣AP﹣C的大小；‎ ‎（Ⅲ）求点C到平面APB的距离．‎ ‎17．（13分）甲、乙等五名奥运志愿者被随机地分到A，B，C，D四个不同的岗位服务，每个岗位至少有一名志愿者．‎ ‎（Ⅰ）求甲、乙两人同时参加A岗位服务的概率；‎ ‎（Ⅱ）求甲、乙两人不在同一个岗位服务的概率；‎ ‎（Ⅲ）设随机变量ξ为这五名志愿者中参加A岗位服务的人数，求ξ的分布列．‎ ‎18．（13分）已知函数，求导函数f′（x），并确定f（x）的单调区间．‎ ‎19．（14分）已知菱形ABCD的顶点A，C在椭圆x2+3y2=4上，对角线BD所在直线的斜率为1．‎ ‎（Ⅰ）当直线BD过点（0，1）时，求直线AC的方程；‎ ‎（Ⅱ）当∠ABC=60°时，求菱形ABCD面积的最大值．‎ ‎20．（13分）对于每项均是正整数的数列A：a1，a2，…，an，定义变换T1，T1将数列A变换成数列T1（A）：n，a1﹣1，a2﹣1，…，an﹣1；对于每项均是非负整数的数列B：b1，b2，…，bm，定义变换T2，T2将数列B各项从大到小排列，然后去掉所有为零的项，得到数列T2（B）；又定义S（B）=2（b1+2b2+…+mbm）+b12+b22+…+bm2．设A0是每项均为正整数的有穷数列，令Ak+1=T2（T1（Ak））（k=0，1，2，…）．‎ ‎（Ⅰ）如果数列A0为5，3，2，写出数列A1，A2；‎ ‎（Ⅱ）对于每项均是正整数的有穷数列A，证明S（T1（A））=S（A）；‎ ‎（Ⅲ）证明：对于任意给定的每项均为正整数的有穷数列A0，存在正整数K，当k≥K时，S（Ak+1）=S（Ak）．‎ ‎　‎ ‎2008年北京市高考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（共8小题，每小题5分，满分40分）‎ ‎1．（5分）（2008•北京）已知全集U=R，集合A={x|﹣2≤x＜3}，B={x|x＜﹣1或x≥4}，那么集合A∩B等于（　　）‎ A．{x|﹣1＜x＜3} B．{x|x≤﹣1或x＞3} C．{x|﹣2≤x＜﹣1} D．{x|﹣1≤x＜3}‎ ‎【分析】由题意全集U=R，集合A={x|﹣2≤x＜3}，B={x|x＜﹣1或x≥4}，根据交集的定义计算A∩B．‎ ‎【解答】解：∵集合A={x|﹣2≤x＜3}，B={x|x＜﹣1或x≥4}，‎ ‎∴集合A∩B={x|﹣2≤x＜﹣1}，‎ 故选C．‎ ‎　‎ ‎2．（5分）（2008•北京）若a=20.5，b=logπ3，c=log2sin，则（　　）‎ A．a＞b＞c B．b＞a＞c C．c＞a＞b D．b＞c＞a ‎【分析】利用估值法知a大于1，b在0与1之间，c小于0．‎ ‎【解答】解：，‎ 由指对函数的图象可知：a＞1，0＜b＜1，c＜0，‎ 故选A ‎　‎ ‎3．（5分）（2008•北京）“函数f（x）（x∈R）存在反函数”是“函数f（x）在R上为增函数”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【分析】函数f（x）（x∈‎ R）存在反函数，至少还有可能函数f（x）在R上为减函数，充分条件不成立；而必要条件显然成立 ‎【解答】解：“函数f（x）在R上为增函数”⇒“函数f（x）（x∈R）存在反函数”；‎ 反之取f（x）=﹣x（x∈R），则函数f（x）（x∈R）存在反函数，但是f（x）在R上为减函数．‎ 故选B ‎　‎ ‎4．（5分）（2008•北京）若点P到直线x=﹣1的距离比它到点（2，0）的距离小1，则点P的轨迹为（　　）‎ A．圆 B．椭圆 C．双曲线 D．抛物线 ‎【分析】把直线x=﹣1向左平移一个单位变为x=﹣2，此时点P到直线x=﹣2的距离等于它到点（2，0）的距离，这就是抛物线的定义．‎ ‎【解答】解：因为点P到直线x=﹣1的距离比它到点（2，0）的距离小1，‎ 所以点P到直线x=﹣2的距离等于它到点（2，0）的距离，‎ 因此点P的轨迹为抛物线．‎ 故选D．‎ ‎　‎ ‎5．（5分）（2008•北京）若实数x，y满足则z=3x+2y的最小值是（　　）‎ A．0 B．1 C． D．9‎ ‎【分析】本题考查的知识点是线性规划，处理的思路为：根据已知的约束条件画出满足约束条件的可行域，再用角点法，求出目标函数的最大值．‎ ‎【解答】解：约束条件对应的平面区域如图示：由图可知当x=0，y=0时，目标函数Z有最小值，‎ Zmin=3x+2y=30=1‎ 故选B ‎　‎ ‎6．（5分）（2008•北京）已知数列{an}对任意的p，q∈N*满足ap+q=ap+aq，且a2=﹣6，那么a10等于（　　）‎ A．﹣165 B．﹣33 C．﹣30 D．﹣21‎ ‎【分析】根据题目所给的恒成立的式子ap+q=ap+aq，给任意的p，q∈N*，我们可以先算出a4，再算出a8，最后算出a10，也可以用其他的赋值过程，但解题的原理是一样的．‎ ‎【解答】解：∵a4=a2+a2=﹣12，‎ ‎∴a8=a4+a4=﹣24，‎ ‎∴a10=a8+a2=﹣30，‎ 故选C ‎　‎ ‎7．（5分）（2008•北京）过直线y=x上的一点作圆（x﹣5）2+（y﹣1）2=2的两条切线l1，l2，当直线l1，l2关于y=x对称时，它们之间的夹角为（　　）‎ A．30° B．45° C．60° D．90°‎ ‎【分析】过圆心M作直线l：y=x的垂线交于N点，过N点作圆的切线能够满足条件，不难求出夹角为600．‎ 明白N点后，用图象法解之也很方便 ‎【解答】解：圆（x﹣5）2+（y﹣1）2=2的圆心（5，1），过（5，1）与y=x垂直的直线方程：x+y﹣6=0，它与y=x 的交点N（3，3），‎ N到（5，1）距离是，两条切线l1，l2，它们之间的夹角为60°．‎ 故选C．‎ ‎　‎ ‎8．（5分）（2008•北京）如图，动点P在正方体ABCD﹣A1B1C1D1的对角线BD1上．过点P作垂直于平面BB1D1D的直线，与正方体表面相交于M，N．设BP=x，MN=y，则函数y=f（x）的图象大致是（　　）‎ A． B． C． D．‎ ‎【分析】只有当P移动到正方体中心O时，MN有唯一的最大值，则淘汰选项A、C；P点移动时，x与y的关系应该是线性的，则淘汰选项D．‎ ‎【解答】解：设正方体的棱长为1，显然，当P移动到对角线BD1的中点O时，函数取得唯一最大值，所以排除A、C；‎ 当P在BO上时，分别过M、N、P作底面的垂线，垂足分别为M1、N1、P1，‎ 则y=MN=M1N1=2BP1=2•xcos∠D1BD=2•是一次函数，所以排除D．‎ 故选B．‎ ‎　‎ 二、填空题（共6小题，每小题5分，满分30分）‎ ‎9．（5分）（2008•北京）已知（a﹣i）2=2i，其中i是虚数单位，那么实数a=　﹣1　．‎ ‎【分析】直接化简方程，利用复数相等条件即可求解．‎ ‎【解答】解：a2﹣2ai﹣1=a2﹣1﹣2ai=2i，a=﹣1‎ 故答案为：﹣1‎ ‎　‎ ‎10．（5分）（2008•北京）已知向量与的夹角为120°，且，那么的值为　0　．‎ ‎【分析】由向量数量积公式进行计算即可．‎ ‎【解答】解：由题意知==2×4×4cos120°+42=0．‎ 故答案为0．‎ ‎　‎ ‎11．（5分）（2008•北京）若展开式的各项系数之和为32，则n=　5　，其展开式中的常数项为 　10　．（用数字作答）‎ ‎【分析】显然展开式的各项系数之和就是二项式系数之和，也即n=5；将5拆分成“前3后2”恰好出现常数项，C52=10．‎ ‎【解答】解：∵展开式的各项系数之和为32‎ ‎∴2n=32解得n=5‎ 展开式的通项为Tr+1=C5rx10﹣5r 当r=2时，常数项为C52=10．‎ 故答案为5，10．‎ ‎　‎ ‎12．（5分）（2008•北京）如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f（f（0））=　2　；=　﹣2　．（用数字作答）‎ ‎【分析】由函数的图象可知，，当0≤x≤‎ ‎2，f'（x）=﹣2，所以由导数的几何意义知=f'（1）=﹣2．‎ ‎【解答】解：∵f（0）=4，f（4）=2，f（2）=4，‎ ‎∴由函数的图象可知，‎ ‎，‎ 由导数的几何意义知=f′（1）=﹣2．‎ 答案：2；﹣2．‎ ‎　‎ ‎13．（5分）（2008•北京）已知函数f（x）=x2﹣cosx，对于[﹣，]上的任意x1，x2，有如下条件：‎ ‎①x1＞x2；②x12＞x22；③|x1|＞x2．‎ 其中能使f（x1）＞f（x2）恒成立的条件序号是　②　．‎ ‎【分析】先研究函数的性质，观察知函数是个偶函数，由于f′（x）=2x+sinx，在[0，]上f′（x）＞0，可推断出函数在y轴两边是左减右增，此类函数的特点是自变量离原点的位置越近，则函数值越小，欲使f（x1）＞f（x2）恒成立，只需x1，到原点的距离比x2，到原点的距离大即可，由此可得出|x1|＞|x2|，在所给三个条件中找符合条件的即可．‎ ‎【解答】解：函数f（x）为偶函数，f′（x）=2x+sinx，‎ 当0＜x≤时，0＜sinx≤1，0＜2x≤π，‎ ‎∴f′（x）＞0，函数f（x）在[0，]上为单调增函数，‎ 由偶函数性质知函数在[﹣，0]上为减函数．‎ 当x12＞x22时，得|x1|＞|x2|≥0，‎ ‎∴f（|x1|）＞f（|x2|），由函数f（x）在上[﹣，]为偶函数得f（x1）＞f（x2），故②成立．‎ ‎∵＞﹣，而f（）=f（），‎ ‎∴①不成立，同理可知③不成立．故答案是②．‎ 故应填②‎ ‎　‎ ‎14．（5分）（2008•北京）某校数学课外小组在坐标纸上，为学校的一块空地设计植树方案如下：第k棵树种植在点Pk（xk，yk）处，其中x1=1，y1=1，当k≥2时，T（a）表示非负实数a的整数部分，例如T（2.6）=2，T（0.2）=0．按此方案，第6棵树种植点的坐标应为　（1，2）　；第2009棵树种植点的坐标应为　（4，402）　．‎ ‎【分析】由题意可知，数列xn为1，2，3，4，5，1，2，3，4，5，1，2，3，4，5，…；数列{yn}为1，1，1，1，1，2，2，2，2，2，3，3，3，3，3，4，4，4，4，4，…由此入手能够得到第6棵树种植点的坐标和第2009棵树种植点的坐标．‎ ‎【解答】解：∵组成的数列为0，0，0，0，1，0，0，0，0，1，0，0，0，0，1…，k=2，3，4，5，…‎ 一一代入计算得数列xn为1，2，3，4，5，1，2，3，4，5，1，2，3，4，5，…‎ 即xn的重复规律是x5n+1=1，x5n+2=2，x5n+3=3，x5n+4=4，x5n=5．n∈N*．‎ 数列{yn}为1，1，1，1，1，2，2，2，2，2，3，3，3，3，3，4，4，4，4，4，…‎ 即yn的重复规律是y5n+k=n，0≤k＜5．‎ ‎∴由题意可知第6棵树种植点的坐标应为（1，2）；第2009棵树种植点的坐标应为（4，402）．‎ ‎　‎ 三、解答题（共6小题，满分80分）‎ ‎15．（13分）（2008•北京）已知函数f（x）=sin2ωx+sinωxsin（ωx+）（ω＞0）的最小正周期为π．‎ ‎（1）求ω的值；‎ ‎（2）求函数f（x）在区间[0，]上的取值范围．‎ ‎【分析】（Ⅰ）先根据倍角公式和两角和公式，对函数进行化简，再利用T=，进而求得ω ‎（Ⅱ）由（Ⅰ）可得函数f（x）的解析式，再根据正弦函数的单调性进而求得函数f（x）的范围．‎ ‎【解答】解：（Ⅰ）==．‎ ‎∵函数f（x）的最小正周期为π，且ω＞0，‎ ‎∴，解得ω=1．‎ ‎（Ⅱ）由（Ⅰ）得．‎ ‎∵，‎ ‎∴，‎ ‎∴．‎ ‎∴，即f（x）的取值范围为．‎ ‎　‎ ‎16．（14分）（2008•北京）如图，在三棱锥P﹣ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC．‎ ‎（Ⅰ）求证：PC⊥AB；‎ ‎（Ⅱ）求二面角B﹣AP﹣C的大小；‎ ‎（Ⅲ）求点C到平面APB的距离．‎ ‎【分析】（Ⅰ）欲证PC⊥AB，取AB中点D，连接PD，CD，可先证AB⊥平面PCD，欲证AB⊥‎ 平面PCD，根据直线与平面垂直的判定定理可知只需证AB与平面PCD内两相交直线垂直，而PD⊥AB，CD⊥AB，又PD∩CD=D，满足定理条件；‎ ‎（Ⅱ）取AP中点E．连接BE，CE，根据二面角平面角的定义可知∠BEC是二面角B﹣AP﹣C的平面角，在△BCE中求出此角即可；‎ ‎（Ⅲ）过C作CH⊥PD，垂足为H，易知CH的长即为点C到平面APB的距离，在Rt△PCD中利用勾股定理等知识求出CH即可．‎ ‎【解答】解：（Ⅰ）取AB中点D，连接PD，CD．‎ ‎∵AP=BP，∴PD⊥AB．‎ ‎∵AC=BC，∴CD⊥AB．‎ ‎∵PD∩CD=D，∴AB⊥平面PCD．‎ ‎∵PC⊂平面PCD，∴PC⊥AB．‎ ‎（Ⅱ）∵AC=BC，AP=BP，∴△APC≌△BPC．‎ 又PC⊥AC，∴PC⊥BC．‎ 又∠ACB=90°，即AC⊥BC，且AC∩PC=C，∴BC⊥平面PAC．‎ 取AP中点E．连接BE，CE．‎ ‎∵AB=BP，∴BE⊥AP．‎ ‎∵EC是BE在平面PAC内的射影，∴CE⊥AP．‎ ‎∴∠BEC是二面角B﹣AP﹣C的平面角．‎ 在△BCE中，BC=2，，CE=‎ cos∠BEC=．∴二面角B﹣AP﹣C的大小arccos．‎ ‎（Ⅲ）由（Ⅰ）知AB⊥平面PCD，∴平面APB⊥平面PCD．‎ 过C作CH⊥PD，垂足为H．‎ ‎∵平面APB∩平面PCD=PD，∴CH⊥平面APB．‎ ‎∴CH的长即为点C到平面APB的距离．‎ 由（Ⅰ）知PC⊥AB，又PC⊥AC，且AB∩AC=A，∴PC⊥平面ABC．‎ ‎∵CD⊂平面ABC，∴PC⊥CD．‎ 在Rt△PCD中，，，‎ ‎∴．∴．‎ ‎∴点C到平面APB的距离为．‎ ‎　‎ ‎17．（13分）（2008•北京）甲、乙等五名奥运志愿者被随机地分到A，B，C，D四个不同的岗位服务，每个岗位至少有一名志愿者．‎ ‎（Ⅰ）求甲、乙两人同时参加A岗位服务的概率；‎ ‎（Ⅱ）求甲、乙两人不在同一个岗位服务的概率；‎ ‎（Ⅲ）设随机变量ξ为这五名志愿者中参加A岗位服务的人数，求ξ的分布列．‎ ‎【分析】（Ⅰ）甲、乙两人同时参加A岗位服务，则另外三个人在B、C、D三个位置进行全排列，所有的事件数是从5个人中选2个作为一组，同其他3人共4个元素在四个位置进行排列．‎ ‎（Ⅱ）总事件数同第一问一样，甲、乙两人不在同一个岗位服务的对立事件是甲、乙两人同时参加同一岗位服务，即甲、乙两人作为一个元素同其他三个元素进行全排列．‎ ‎（Ⅲ）五名志愿者中参加A岗位服务的人数ξ可能的取值是1、2，ξ=2”是指有两人同时参加A岗位服务，同第一问类似做出结果．写出分布列．‎ ‎【解答】解：（Ⅰ）记甲、乙两人同时参加A岗位服务为事件EA，‎ 总事件数是从5个人中选2个作为一组，同其他3人共4个元素在四个位置进行排列C52A44．‎ 满足条件的事件数是A33，‎ 那么，‎ 即甲、乙两人同时参加A岗位服务的概率是．‎ ‎（Ⅱ）记甲、乙两人同时参加同一岗位服务为事件E，‎ 满足条件的事件数是A44，‎ 那么，‎ ‎∴甲、乙两人不在同一岗位服务的概率是．‎ ‎（Ⅲ）随机变量ξ可能取的值为1，2．事件“ξ=2”是指有两人同时参加A岗位服务，‎ 则．‎ ‎∴，ξ的分布列是 ‎ ‎ ξ ‎ 1‎ ‎ 2‎ ‎ P ‎　‎ ‎18．（13分）（2008•北京）已知函数，求导函数f′（x），并确定f（x）的单调区间．‎ ‎【分析】根据函数的求导法则进行求导，然后由导数大于0时原函数单调递增，导数小于0时原函数单调递减可得答案．‎ ‎【解答】解：==‎ ‎．‎ 令f'（x）=0，得x=b﹣1．‎ 当b﹣1＜1，即b＜2时，f'（x）的变化情况如下表：‎ x ‎（﹣∞，b﹣1）‎ b﹣1‎ ‎（b﹣1，1）‎ ‎（1，+∞）‎ f′（x）‎ ‎﹣‎ ‎0‎ ‎+‎ ‎﹣‎ 当b﹣1＞1，即b＞2时，f'（x）的变化情况如下表：‎ x ‎（﹣∞，1）‎ ‎（1，b﹣1）‎ b﹣1‎ ‎（b﹣1，+∞）‎ f′（x）‎ ‎﹣‎ ‎+‎ ‎0‎ ‎﹣‎ 所以，当b＜2时，函数f（x）在（﹣∞，b﹣1）上单调递减，在（b﹣1，1）上单调递增，‎ 在（1，+∞）上单调递减．‎ 当b＞2时，函数f（x）在（﹣∞，1）上单调递减，在（1，b﹣1）上单调递增，在（b﹣1，+∞）上单调递减．‎ 当b﹣1=1，即b=2时，，所以函数f（x）在（﹣∞，1）上单调递减，在（1，+∞）上单调递减．‎ ‎　‎ ‎19．（14分）（2008•北京）已知菱形ABCD的顶点A，C在椭圆x2+3y2=4上，对角线BD所在直线的斜率为1．‎ ‎（Ⅰ）当直线BD过点（0，1）时，求直线AC的方程；‎ ‎（Ⅱ）当∠ABC=60°时，求菱形ABCD面积的最大值．‎ ‎【分析】（Ⅰ）由题意得直线BD的方程，根据四边形ABCD为菱形，判断出AC⊥‎ BD．于是可设出直线AC的方程与椭圆的方程联立，根据判别式大于0求得n的范围，设A，C两点坐标分别为（x1，y1），（x2，y2），根据韦达定理求得x1+x2和x1x2，代入直线方程可表示出y1+y2，进而可得AC中点的坐标，把中点代入直线y=x+1求得n，进而可得直线AC的方程．‎ ‎（Ⅱ）根据四边形ABCD为菱形判断出∠ABC=60°且|AB|=|BC|=|CA|．进而可得菱形ABCD的面积根据n的范围确定面积的最大值．‎ ‎【解答】解：（Ⅰ）由题意得直线BD的方程为y=x+1．‎ 因为四边形ABCD为菱形，所以AC⊥BD．‎ 于是可设直线AC的方程为y=﹣x+n．‎ 由得4x2﹣6nx+3n2﹣4=0．‎ 因为A，C在椭圆上，‎ 所以△=﹣12n2+64＞0，解得．‎ 设A，C两点坐标分别为（x1，y1），（x2，y2），‎ 则，，y1=﹣x1+n，y2=﹣x2+n．‎ 所以．‎ 所以AC的中点坐标为．‎ 由四边形ABCD为菱形可知，点在直线y=x+1上，‎ 所以，解得n=﹣2．‎ 所以直线AC的方程为y=﹣x﹣2，即x+y+2=0．‎ ‎（Ⅱ）因为四边形ABCD为菱形，且∠ABC=60°，‎ 所以|AB|=|BC|=|CA|．‎ 所以菱形ABCD的面积．‎ 由（Ⅰ）可得，‎ 所以．‎ 所以当n=0时，菱形ABCD的面积取得最大值．‎ ‎　‎ ‎20．（13分）（2008•北京）对于每项均是正整数的数列A：a1，a2，…，an，定义变换T1，T1将数列A变换成数列T1（A）：n，a1﹣1，a2﹣1，…，an﹣1；对于每项均是非负整数的数列B：b1，b2，…，bm，定义变换T2，T2将数列B各项从大到小排列，然后去掉所有为零的项，得到数列T2（B）；又定义S（B）=2（b1+2b2+…+mbm）+b12+b22+…+bm2．设A0是每项均为正整数的有穷数列，令Ak+1=T2（T1（Ak））（k=0，1，2，…）．‎ ‎（Ⅰ）如果数列A0为5，3，2，写出数列A1，A2；‎ ‎（Ⅱ）对于每项均是正整数的有穷数列A，证明S（T1（A））=S（A）；‎ ‎（Ⅲ）证明：对于任意给定的每项均为正整数的有穷数列A0，存在正整数K，当k≥K时，S（Ak+1）=S（Ak）．‎ ‎【分析】（Ⅰ）由A0：5，3，2，求得T1（A0）再通过Ak+1=T2（T1（Ak））求解．‎ ‎（Ⅱ）设有穷数列A求得T1（A）再求得S（T1（A）），由S（A）=2（a1+2a2++nan）+a12+a22++an2，两者作差比较．‎ ‎（Ⅲ）设A是每项均为非负整数的数列a1，a2，an．在存在1≤i＜j≤n，有ai≤aj时条件下，交换数列A的第i项与第j项得到数列B，在存在1≤m＜n，使得am+1=am+2═an=0时条件下，若记数列a1，a2，…，am为C，Ak+1=T2（T1（Ak））s（Ak+1）≤S（T1（Ak））．由S（T1（Ak））=S（Ak），得到S（Ak+1）≤S（Ak）．S（Ak）是大于2的整数，所以经过有限步后，必有S（Ak）=S（Ak+1）=S（Ak+2）=0．‎ ‎【解答】解：（Ⅰ）解：A0：5，3，2，T1（A0）：3，4，2，1，A1=T2（T1（A0））：4，3，2，1；T1（A1）：4，3，2，1，0，A2=T2（T1（A1））：4，3，2，1．‎ ‎（Ⅱ）证明：设每项均是正整数的有穷数列A为a1，a2，an，‎ 则T1（A）为n，a1﹣1，a2﹣1，an﹣1，‎ 从而S（T1（A））=2[n+2（a1﹣1）+3（a2﹣1）++（n+1）（an﹣1）]+n2+（a1﹣1）2+（a2﹣1）2++（an﹣1）2．‎ 又S（A）=2（a1+2a2++nan）+a12+a22++an2，‎ 所以S（T1（A））﹣S（A）=2[n﹣2﹣3﹣﹣（n+1）]+2（a1+a2++an）+n2﹣2（a1+a2++an）+n=﹣n（n+1）+n2+n=0，‎ 故S（T1（A））=S（A）．‎ ‎（Ⅲ）证明：设A是每项均为非负整数的数列a1，a2，an．‎ 当存在1≤i＜j≤n，使得ai≤aj时，交换数列A的第i项与第j项得到数列B，‎ 则S（B）﹣S（A）=2（iaj+jai﹣iai﹣jaj）=2（i﹣j）（aj﹣ai）≤0．‎ 当存在1≤m＜n，使得am+1=am+2═an=0时，若记数列a1，a2，am为C，‎ 则S（C）=S（A）．‎ 所以S（T2（A））≤S（A）．‎ 从而对于任意给定的数列A0，由Ak+1=T2（T1（Ak））（k=0，1，2，）‎ 可知S（Ak+1）≤S（T1（Ak））．‎ 又由（Ⅱ）可知S（T1（Ak））=S（Ak），所以S（Ak+1）≤S（Ak）．‎ 即对于k∈N，要么有S（Ak+1）=S（Ak），要么有S（Ak+1）≤S（Ak）﹣1．‎ 因为S（Ak）是大于2的整数，所以经过有限步后，必有S（Ak）=S（Ak+1）=S（Ak+2）=0．‎ 即存在正整数K，当k≥K时，S（Ak+1）=S（A）‎ ‎　‎ 参与本试卷答题和审题的老师有：zhiyuan；wdlxh；wzj123；豫汝王世崇；涨停；qiss；minqi5；zlzhan；xintrl；wsj1012；zhwsd；wodeqing（排名不分先后）‎ 菁优网 ‎2017年2月4日