2014山东省淄博市中考数学试卷

2014山东省淄博市中考数学试卷

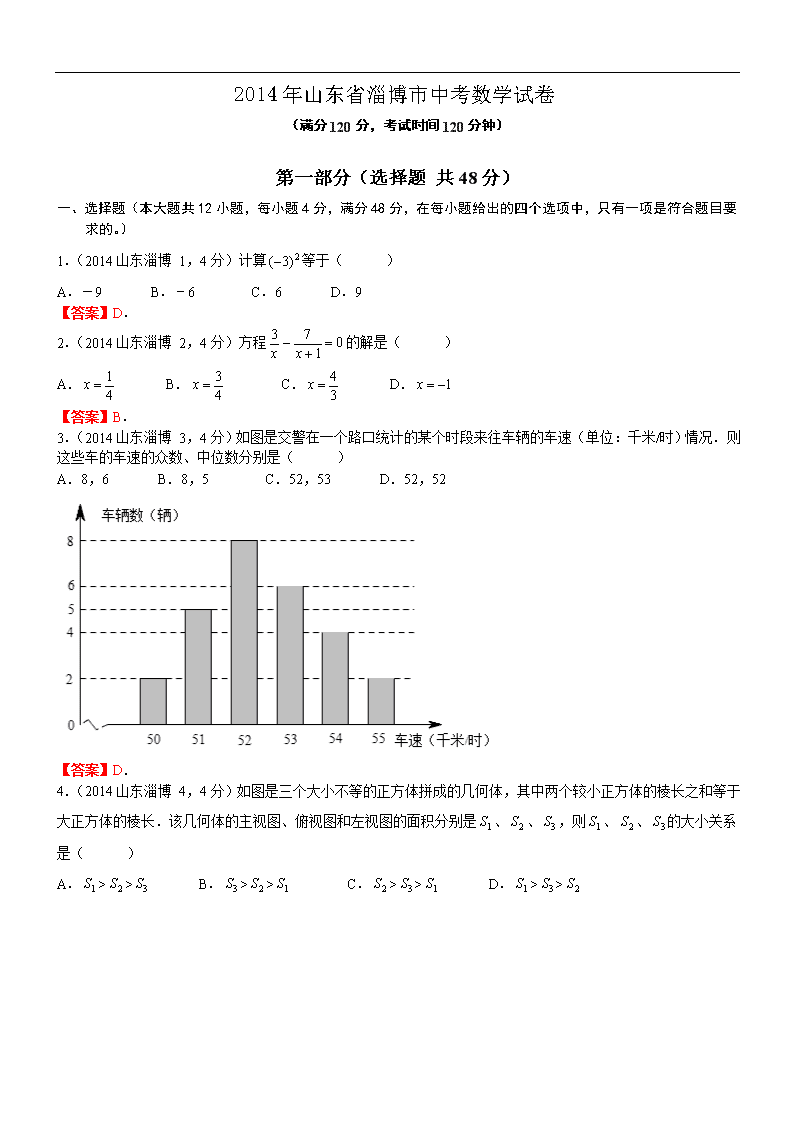
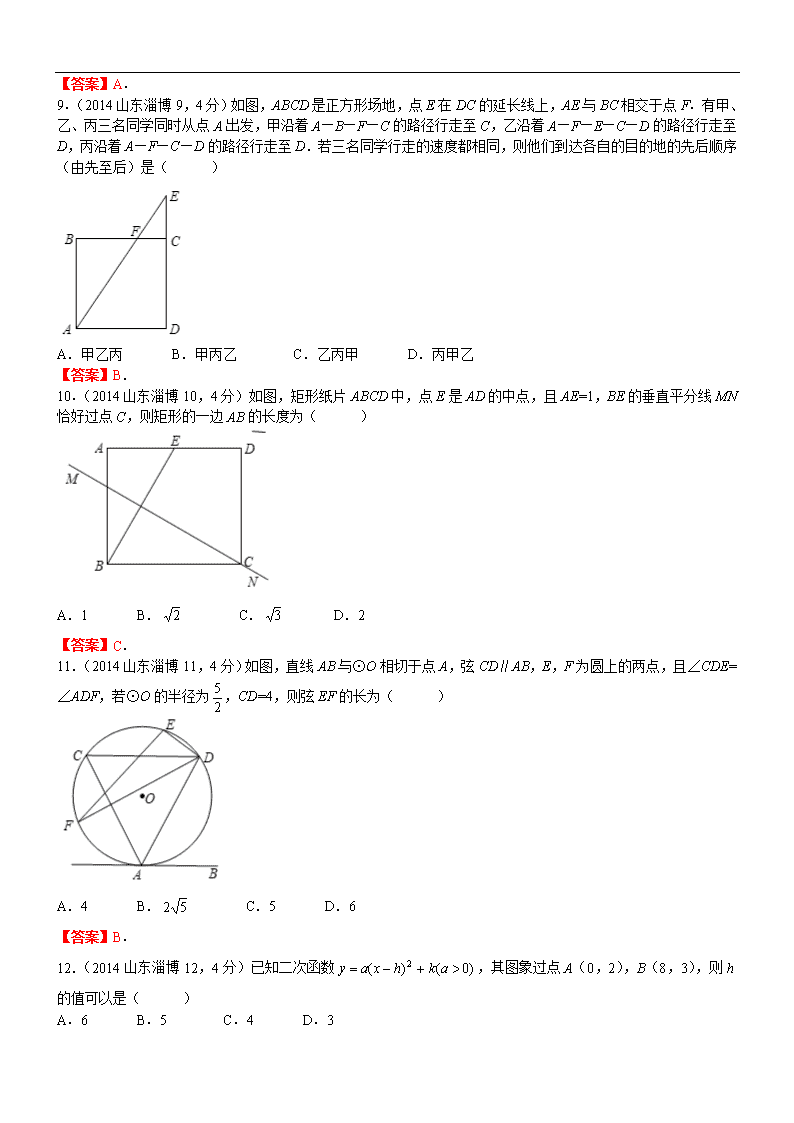
‎2014年山东省淄博市中考数学试卷 ‎（满分120分，考试时间120分钟）‎ 第一部分（选择题 共48分）‎ 一、选择题（本大题共12小题，每小题4分，满分48分，在每小题给出的四个选项中，只有一项是符合题目要求的。）‎ ‎1．（2014山东淄博 1，4分）计算等于（ ）‎ A．－9 B．﹣6 C．6 D．9‎ ‎【答案】D．‎ ‎2．（2014山东淄博 2，4分）方程的解是（ ）‎ A． B． C． D．‎ ‎【答案】B．‎ ‎3．（2014山东淄博 3，4分）如图是交警在一个路口统计的某个时段来往车辆的车速（单位：千米/时）情况．则这些车的车速的众数、中位数分别是（ ）‎ A．8，6 B．8，5 C．52，53 D．52，52‎ ‎【答案】D．‎ ‎4．（2014山东淄博 4，4分）如图是三个大小不等的正方体拼成的几何体，其中两个较小正方体的棱长之和等于大正方体的棱长．该几何体的主视图、俯视图和左视图的面积分别是、、，则、、的大小关系是（ ）‎ A．>> B．>> C．>> D．>>‎ ‎【答案】D．‎ ‎5．（2014山东淄博5，4分）一元二次方程的根是（ ）‎ A． B．， C．， D．，‎ ‎【答案】C．‎ ‎6．（2014山东淄博6，4分）当时，代数式的值是7．则当时，这个代数式的值是（ ）‎ A．7 B．3 C．1 D．﹣7‎ ‎【答案】C．‎ ‎7．（2014山东淄博7，4分）如图，等腰梯形ABCD中，对角线AC，DB相交于点P，∠BAC=∠CDB=90°，AB=AD=DC，则cos∠DPC的值是（ ）‎ A． B． C． D．‎ ‎【答案】A．‎ ‎8．（2014山东淄博8，4分）如图，二次函数的图象过点B（0，﹣2），它与反比例函数的图象交于点A（m，4），则这个二次函数的解析式为（ ）‎ A． B． C． D．‎ ‎【答案】A．‎ ‎9．（2014山东淄博9，4分）如图，ABCD是正方形场地，点E在DC的延长线上，AE与BC相交于点F．有甲、乙、丙三名同学同时从点A出发，甲沿着A—B—F—C的路径行走至C，乙沿着A—F—E—C—D的路径行走至D，丙沿着A—F—C—D的路径行走至D．若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序（由先至后）是（ ）‎ A．甲乙丙 B．甲丙乙 C．乙丙甲 D．丙甲乙 ‎【答案】B．‎ ‎10．（2014山东淄博10，4分）如图，矩形纸片ABCD中，点E是AD的中点，且AE=1，BE的垂直平分线MN恰好过点C，则矩形的一边AB的长度为（ ）‎ A．1 B． C． D．2‎ ‎【答案】C．‎ ‎11．（2014山东淄博11，4分）如图，直线AB与⊙O相切于点A，弦CD∥AB，E，F为圆上的两点，且∠CDE=∠ADF，若⊙O的半径为，CD=4，则弦EF的长为（ ）‎ A．4 B． C．5 D．6‎ ‎【答案】B．‎ ‎12．（2014山东淄博12，4分）已知二次函数，其图象过点A（0，2），B（8，3），则h的值可以是（ ）‎ A．6 B．5 C．4 D．3‎ ‎【答案】D．‎ 第二部分（非选择题 共72分）‎ 二、填空题（本大题共5小题，每小题4分，满分20分.）‎ ‎13．（2014山东淄博13，4分）分解因式： ．‎ ‎【答案】．‎ ‎14．（2014山东淄博14，4分）某实验中学九年级（1）班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示，其中评价为“A”所在扇形的圆心角是 度．‎ ‎【答案】108．‎ ‎15．（2014山东淄博15，4分）已知□ABCD，对角线AC，BD相交于点O，请你添加一个适当的条件，使□ABCD成为一个菱形．你添加的条件是 ．‎ ‎【答案】AB=BC或AC⊥BD等．‎ ‎16．（2014山东淄博16，4分）关于x的反比例函数的图象如图所示，A，P为该图象上的点，且关于原点成中心对称．△PAB中，PB∥y轴，AB∥x轴，PB与AB相交于点B．若△PAB的面积大于12，则关于x的方程的根的情况是是 ．‎ ‎【答案】没有实数根．‎ ‎17．（2014山东淄博17，4分）如图，在正方形网格中有一边长为4的平行四边形ABCD，请将其剪拼成一个有一边长为6的矩形．（要求：在答题卡的图中画出裁剪线即可）．‎ ‎【答案】‎ 三、解答题（本大题共7小题，满分52分，解答应写出文字说明、证明过程或演算步骤）‎ ‎18．（2014山东淄博18，5分）‎ 计算：．‎ ‎【答案】解：原式=‎ ‎＝．‎ ‎19．（2014山东淄博19，5分）‎ 如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1=55°，求∠2的度数．‎ ‎【答案】‎ 解：∵AB⊥BC，‎ ‎∴∠1+∠3=90°．‎ ‎∵∠1=55°，‎ ‎∴∠3=35°．‎ ‎∵a∥b，‎ ‎∴∠2=∠3=35°．‎ ‎20．（2014山东淄博20，8分）‎ 节能灯根据使用寿命分成优等品、正品和次品三个等级，其中使用寿命大于或等于8000小时的节能灯是优等品，使用寿命小于6000小时的节能灯是次品，其余的节能灯是正品，质监部门对某批次的一种节能灯（共200个）的使用寿命进行追踪调查，并将结果整理成下表．‎ 寿命（小时 频数 频率 ‎4000≤t<5000‎ ‎10‎ ‎0.05‎ ‎5000≤t<6000‎ ‎20‎ a ‎6000≤t<7000‎ ‎80‎ ‎0.40‎ ‎7000≤t<8000‎ b ‎0.15‎ ‎8000≤t<9000‎ ‎60‎ c 合计 ‎200‎ ‎1‎ ‎（1）根据分布表中的数据，在答题卡上写出a，b，c的值；‎ ‎（2）某人从这200个节能灯中随机购买1个，求这种节能灯恰好不是次品的概率．‎ ‎【答案】‎ 解：（1）a=0.1，b=30，c=0.3；‎ ‎（2）这批节能灯中，优等品有60个，正品有110个，次品有30个，此人购买的1个节能灯恰好不是次品的概率为：．‎ ‎21．（2014山东淄博21，8分）‎ 为鼓励居民节约用电，某省试行阶梯电价收费制，具体执行方案如下： ‎ 档 次 每户每月用电数（度）‎ 执行电价（元/度）‎ 第一档 小于等于200‎ ‎0.55‎ 第二档 大于200小于400‎ ‎0.6‎ 第三档 大于等于400‎ ‎0.85‎ 例如：一户居民七月份用电420度，则需缴电费420×0.85=357（元）．‎ 某户居民五、六月份共用电500度，缴电费290.5元．已知该用户六月份用电量大于五月份，且五、六月份的用电量均小于400度．问该户居民五、六月份各用电多少度？‎ ‎【答案】‎ 解：因为两个月用电量为500度，所以每个月用电量不可能都在第一档，假设该用户五月、六月每月用电均超过200度，此时的电费共计：500×0.6=300（元），而300>290.5，不符合题意，又因为六月份用电大于五月份，所以五月份用电在第一档，六月份用电在第二档．‎ 设五月份用电x度，六月份用电y度，根据题意，得：‎ 解得：‎ 答：该户居民五、六月份各用电190度、310度．‎ ‎22．（2014山东淄博22，8分）‎ 如图，在直角坐标系中，点A的坐标是（0，3），点C是x轴上的一个动点，点C在x轴上移动时，始终保持△ACP是等边三角形．当点C移动到点O时，得到等边三角形AOB（此时点P与点B重合）．‎ ‎（1）点C在移动的过程中，当等边三角形ACP的顶点P在第三象限时（如图所示），‎ 求证：△AOC≌△ABP；由此你发现什么结论？‎ ‎（2）求点C在x轴上移动时，点P所在函数图象的解析式．‎ ‎【答案】‎ 解：（1）证明：∵△AOB与△ACP都是等边三角形，‎ ‎∴AO=AB，AC=AP，∠CAP=∠OAB=60°．‎ ‎∴∠CAP+∠PAO=∠OAB+∠PAO．‎ ‎∴∠CAO=∠PAB．‎ ‎∴△AOC≌△ABP．‎ 结论：点P在过点B且与AB垂直的直线上或PA⊥AB或∠ABP=90°．‎ ‎（2）点P所在函数图象是过点B且与AB垂直的直线上，‎ ‎∵△AOB是等边三角形，A（0，3），∴B（，）．‎ 当点C移动到使点P在y轴上时，得P（0，﹣3）．‎ 设点P所在直线的解析式为：，把B，P两点的坐标代入得：‎ ‎∴‎ 解得：‎ 所以点P所在函数图象的解析式为：．‎ ‎23．（2014山东淄博23，9分）‎ 如图，四边形ABCD中，AC⊥BD交BD于点E，点F，M分别是AB，BC的中点，BN平分∠ABE交AM于点N，AB=AC=BD，连接MF，NF．‎ ‎（1）判断△BMN的形状，并证明你的结论；‎ ‎（2）判断△MFN与△BDC之间的关系，并说明理由．‎ ‎【答案】‎ 解：（1）△BMN是等腰直角三角形．‎ 证明：∵AB=AC，点M是BC的中点，‎ ‎∴AM⊥BC，AM平分∠BAC．‎ ‎∵BN平分∠ABE，AC⊥BD，‎ ‎∴∠MNB=∠NAB+∠ABN=（∠BAE+∠ABE）=45°．‎ ‎∴△BMN是等腰直角三角形．‎ ‎（2）△MFN∽△BDC．‎ ‎∵点F，M分别是AB，BC的中点，‎ ‎∴FM∥AC，FM=AC．‎ ‎∵AC=BD，‎ ‎∴FM=BD，即．‎ ‎∴△BMN是等腰直角三角形．‎ ‎∴NM=BM=BC，即．‎ ‎∴．‎ ‎∵AM⊥BC，‎ ‎∴∠NMF+∠FMB=90°．‎ ‎∵FM∥AC，‎ ‎∴FM⊥BE．‎ ‎∴∠CBD+∠FMB=90°．‎ ‎∴∠NMF=∠CBD．‎ ‎∴△MFN∽△BDC．‎ ‎24．（2014山东淄博24，9分）‎ 如图，点A与点B的坐标分别是（1，0），（5，0）点P是该直角坐标系内的一个动点，‎ ‎（1）使∠APB=30°的点P有 个；‎ ‎（2）若点P在y轴上，且∠APB=30°，求满足条件的点P的坐标；‎ ‎（3）当P点在y轴上移动时，∠APB是否有最大值？若有，求点P的坐标，并说明此时∠APB最大的理由；若没有，也请说明理由．‎ ‎【答案】‎ 解：（1）无数个；‎ ‎（2）（2）如下图，当P点在y轴上时，一共有4个点，分别是、、、；‎ 设的坐标为（0，m），过点C分别向x轴、y轴作垂线，垂足分别为点D和点E，在 Rt△ACD中，CA=AB=4，∠CAD=60°，则CD=AC sin60°=6，由辅助线作法可知四边形CEOD为矩形，则OE=CD=，CE=OD=3，则，在Rt△中，由勾股定理可知，，即，整理得，‎ ‎，解得，（舍去），即 ‎，，‎ 因此、、、的坐标依次为、、、．‎ ‎（3）当过点A，B的⊙D与y轴相切于点P时，∠APB最大，如下图，⊙D的半径为3，连接DA，作DE垂直于x轴，垂足为E，得，‎ ‎∴P（0，）．‎ 当点P在y轴负半轴上时，可得P（0，﹣）．‎ 理由：在y轴正半轴上任取一点M（不与点P重合），连接MA，MB，MB交⊙D于点N，连接NA，则 ‎∠APB=∠ANB，‎ ‎∵∠ANB是△BMN的外角，‎ ‎∴∠ANB >∠AMB，‎ ‎∴∠APB >∠AMB．‎ 若点P在y轴的负半轴上，同理可证得∠APB >∠AMB．‎