- 2021-04-13 发布 |
- 37.5 KB |
- 9页


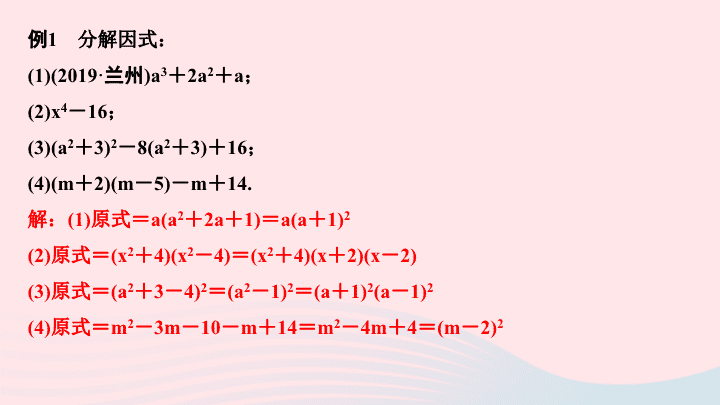
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第12章整式的乘除专题课堂二因式分解课件新版华东师大版
第 12 章 整式的乘除 专题课堂(二) 因式分解 根据多项式的特点灵活选择方法 类型 (1) 有公因式的 ,先提公因式,再考虑公式法; ( 2) 没有公因式 , 且是二项式 , 能化成平方差的形式 , 用平方差公式; (3) 没有公因式 , 且是三项式 , 考虑用完全平方公式; (4) 先做乘法运算并化简 , 再套公式. 例 1 分解因式: (1) (2019· 兰州 ) a 3 + 2a 2 + a ; (2)x 4 - 16 ; (3)(a 2 + 3) 2 - 8(a 2 + 3) + 16 ; (4)(m + 2)(m - 5) - m + 14. 解: (1) 原式= a(a 2 + 2a + 1) = a(a + 1) 2 (2) 原式= (x 2 + 4)(x 2 - 4) = (x 2 + 4)(x + 2)(x - 2) (3) 原式= (a 2 + 3 - 4) 2 = (a 2 - 1) 2 = (a + 1) 2 (a - 1) 2 (4) 原式= m 2 - 3m - 10 - m + 14 = m 2 - 4m + 4 = (m - 2) 2 分析: (1) 先提公因式 , 后套公式; (2) 套平方差公式 , 再重复套一次; (3) 套完全平方公式 , 再套平方差公式; ( 4) 先做乘法并化简 , 再套完全平方公式. 【 对应训练 】 1 .分解因式: (1) (2019 · 内江 ) xy 2 - 2xy + x ; 解:原式= x(y - 1) 2 (2)(x 2 + y 2 ) 2 - 4x 2 y 2 ; 解:原式= (x + y) 2 (x - y) 2 (3)(a 2 + b 2 ) 2 + 4a 2 b 2 - 4ab(a 2 + b 2 ) ; 解:原式= (a - b) 4 (4)9(m + n) 2 - 6(m 2 - n 2 ) + (m - n) 2 ; 解:原式= 4(m + 2n) 2 (5)(2x + 3)(2x - 3) - 2(2x - 5). 解:原式= (2x - 1) 2 因式分解与三角形 类型 (1) 利用因式分解确定三角形的形状; (2) 利用因式分解确定代数式值的正负. 例 2 已知 a , b , c 为△ ABC 的三边长,求证: (a 2 + b 2 - c 2 ) 2 - 4a 2 b 2 < 0. 证明: (a 2 + b 2 - c 2 ) 2 - 4a 2 b 2 = (a 2 + b 2 - c 2 + 2ab)(a 2 + b 2 - c 2 - 2ab) = [(a 2 + 2ab + b 2 ) - c 2 ][(a 2 - 2ab + b 2 ) - c 2 ] = [(a + b) 2 - c 2 ][(a - b) 2 - c 2 ] = (a + b + c)(a + b - c)(a - b + c)(a - b - c) ,∵ a > 0 , b > 0 , c > 0 , a + b > c , a + c > b , a - b < c ,∴ a + b + c > 0 , a + b - c > 0 , a - b + c > 0 , a - b - c < 0 ,∴ (a + b + c)(a + b - c)(a - b + c)(a - b - c) < 0 ,即 (a 2 + b 2 - c 2 ) 2 - 4a 2 b 2 < 0 分析: 先将 (a 2 + b 2 - c 2 ) 2 - 4a 2 b 2 分解因式 , 再根据三角形三边关系确定每个因式的正负 , 从而确定 ( a 2 + b 2 - c 2 ) 2 - 4a 2 b 2 的正负. 【 对应训练 】 2 .已知 a , b , c 是△ ABC 的三边长,且满足 a 2 - 4bc - ab + 4ac = 0 ,求证:△ ABC 为等腰三角形. 证明:∵ a 2 - 4bc - ab + 4ac = 0 ,∴ (a 2 - ab) + (4ac - 4bc) = 0 ,∴ a(a - b) + 4c(a - b) = 0 ,∴ (a - b)(a + 4c) = 0.∵a + 4c > 0 ,∴ a - b = 0 ,∴ a = b ,∴△ ABC 为等腰三角形查看更多