- 2021-04-13 发布 |
- 37.5 KB |
- 15页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
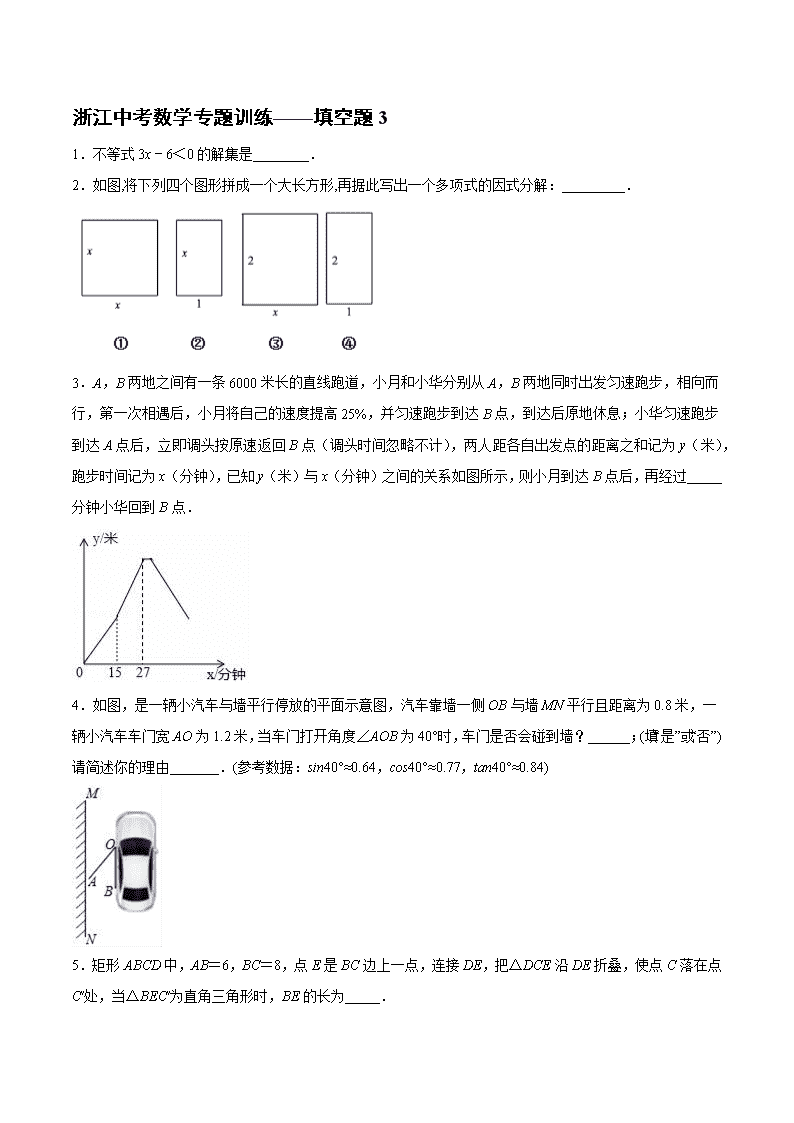
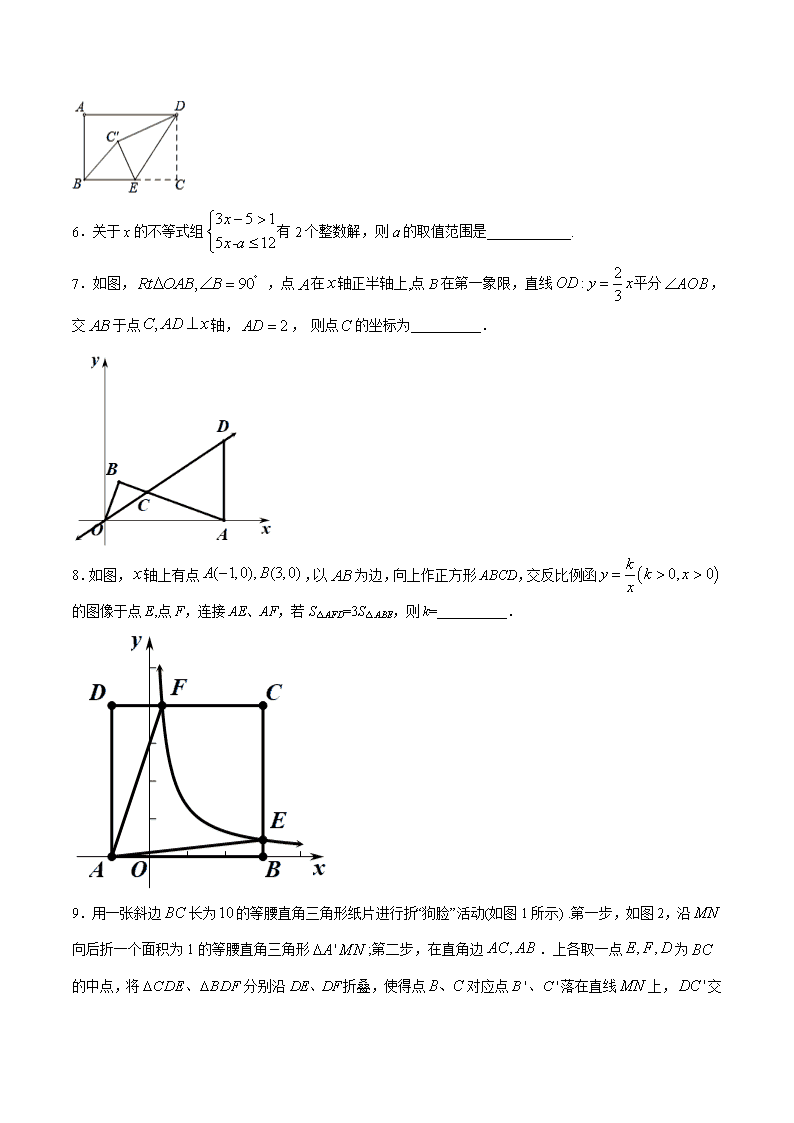
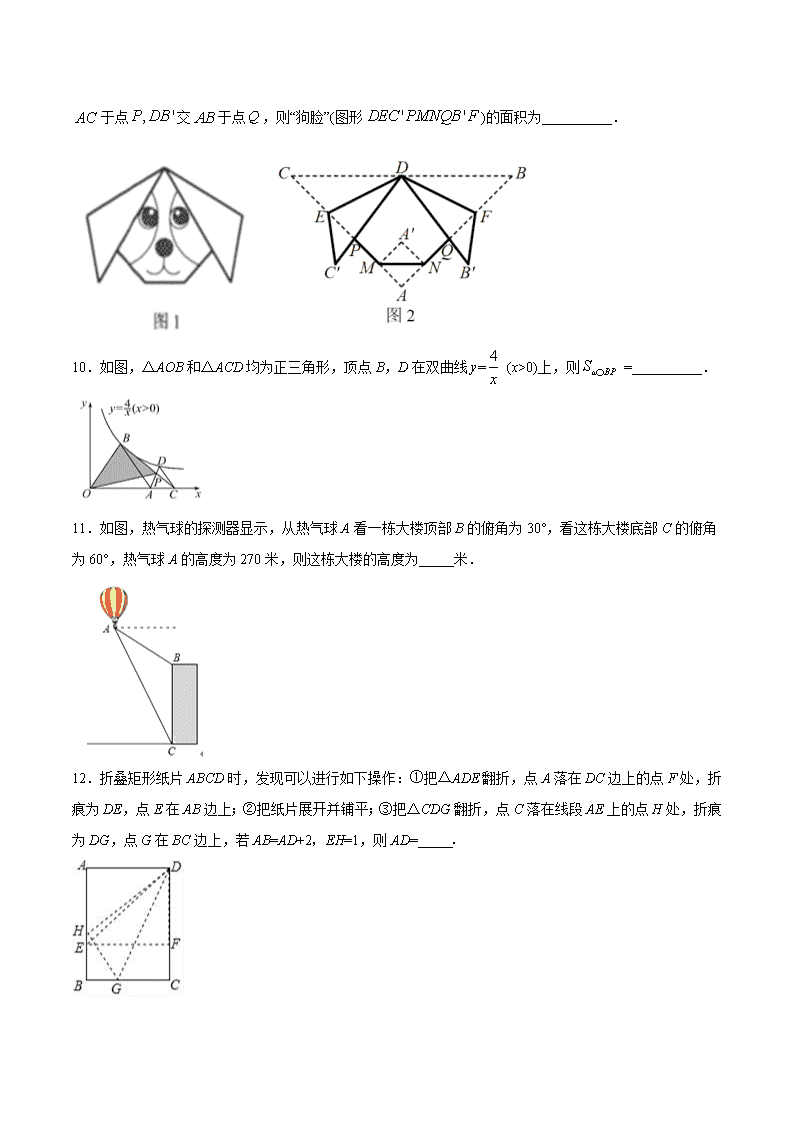
浙江中考数学专题训练——填空题3
浙江中考数学专题训练——填空题3 1.不等式3x﹣6<0的解集是________. 2.如图,将下列四个图形拼成一个大长方形,再据此写出一个多项式的因式分解:_________. 3.A,B两地之间有一条6000米长的直线跑道,小月和小华分别从A,B两地同时出发匀速跑步,相向而行,第一次相遇后,小月将自己的速度提高25%,并匀速跑步到达B点,到达后原地休息;小华匀速跑步到达A点后,立即调头按原速返回B点(调头时间忽略不计),两人距各自出发点的距离之和记为y(米),跑步时间记为x(分钟),已知y(米)与x(分钟)之间的关系如图所示,则小月到达B点后,再经过_____分钟小华回到B点. 4.如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84) 5.矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为_____. 6.关于x的不等式组有2个整数解,则a的取值范围是____________. 7.如图, ,点在轴正半轴上,点在第一象限,直线平分,交于点轴,, 则点的坐标为__________. 8.如图,轴上有点,以为边,向上作正方形ABCD,交反比例函的图像于点E,点F,连接AE、AF,若S△AFD=3S△ABE,则k=__________. 9.用一张斜边长为的等腰直角三角形纸片进行折“狗脸”活动(如图1所示) .第一步,如图2,沿向后折一个面积为1的等腰直角三角形;第二步,在直角边.上各取一点为的中点,将分别沿折叠,使得点对应点落在直线上,交 于点交于点,则“狗脸”(图形)的面积为__________. 10.如图,△AOB和△ACD均为正三角形,顶点B,D在双曲线y= (x>0)上,则 =__________. 11.如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,热气球A的高度为270米,则这栋大楼的高度为_____米. 12.折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在线段AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=_____. 参考答案 1.x<2 【解析】 【分析】 不等式移项,将x系数化为1,即可求出解集. 【详解】 解:3x﹣6<0 移项得:3x<6, 解得:x<2, 故答案是:x<2 【点睛】 考查了解一元一次不等式,熟练掌握解不等式的步骤(①去分母;②去括号;③移项;④合并同类项;⑤系数化为1.)是解本题的关键. 2. 【解析】 【分析】 由图可知拼成的大长方形面积为=,再进行因式分解即可. 【详解】 由图得大长方形的面积为=, 故 【点睛】 此题主要考查因式分解的应用,解题的关键是先求出大长方形的面积. 3.33 【解析】 【分析】 设小月和小华的速度分别为x米/分钟,y米/分钟.构建方程组即可解决问题. 【详解】 设小月和小华的速度分别为x米/分钟,y米/分钟. 由题意:, 解得, ∵12000÷200=60(分钟), 60﹣27=33(分钟). 故答案为33. 【点睛】 本题考查一次函数的应用,二元一次方程组等知识,解题的关键是读懂图象信息,学会利用参数构建方程组解决问题. 4.否, 点A到OB的距离小于OB与墙MN平行且距离 【解析】 【分析】 过点A作AC⊥OB,垂足为点C,解三角形求出AC的长度,进而作出比较即可. 【详解】 过点A作AC⊥OB,垂足为点C, 在Rt△ACO中, ∵∠AOC=40°,AO=1.2米, ∴AC=sin∠AOC•AO≈0.64×1.2=0.768, ∵汽车靠墙一侧OB与墙MN平行且距离为0.8米, ∴车门不会碰到墙(点A到OB的距离小于OB与墙MN平行且距离), 故答案为否,点A到OB的距离小于OB与墙MN平行且距离. 【点睛】 本题主要考查了解直角三角形的应用,解题的关键是正确添加辅助线. 5.2或5. 【解析】 【分析】 分情况讨论:当∠BC′E=90°时,如图1;当∠BEC′=90°时,如图2,分别利用矩形的性质和勾股定理进行计算即可. 【详解】 解:如图1,当∠BC′E=90°时, 在矩形ABCD中,AB=6,AD=BC=8, ∴BD=10, ∵把△DCE沿DE折叠,使点C落在点C′处, ∴∠DC′E=∠C=90°, ∵∠BC′E=90°, ∴B,C′,D三点共线, ∴DC′=DC=6, ∴BC′=4,BE=8﹣C′E, ∵BC′2+EC′2=BE2, ∴42+C′E2=(8﹣C′E)2, 解得C′E=3, ∴BE=8﹣3=5; 如图2,当∠BEC′=90°时, 在矩形ABCD中,AB=CD=6,AD=BC=8, ∵把△DCE沿DE折叠,使点C落在点C′处, ∴∠DC′E=∠C=90°, ∵∠BEC′=90°, ∴∠CEC′=90°, ∵CD=C′D, ∴四边形ECDC′是正方形, ∴C′E=CE=CD=6, ∴BE=8-6=2. 综上所述,当△BEC′为直角三角形时,BE的长为2或5, 故答案为:2或5. 【点睛】 本题考查了折叠的性质、矩形的性质、正方形的判定和性质以及勾股定理等知识,分类讨论各种可能的情况是全面解决问题的关键. 6.8⩽a<13; 【解析】 【分析】 首先确定不等式组的解集,先利用含a的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a的不等式,从而求出a的范围. 【详解】 解不等式3x−5>1,得:x>2, 解不等式5x−a⩽12,得:x⩽ , ∵不等式组有2个整数解, ∴其整数解为3和4, 则4⩽<5, 解得:8⩽a<13, 故答案为:8⩽a<13 【点睛】 此题考查一元一次不等式组的整数解,掌握运算法则是解题关键 7. 【解析】 【分析】 由正比例函数解析式依次得到、、,再根据角平分线的定义和 性质、相似三角形的判定和性质列出关于的方程,解方程即可得解. 【详解】 解:∵直线,轴, ∴当时, ∴ ∴ ∴ 过点作轴于点,如图: ∵点在直线上 ∴设 ∵直线:平分, ∴, ∴ ∴ ∵在和中,, ∴ ∴ ∴ ∴ ∴ ∴ ∴点的坐标为:. 故答案是: 【点睛】 本题考查了正比例函数图象上点的坐标、角平分线的定义和性质、相似三角形的判定和性质、线段的和差以及利用一元一次方程在几何图形中的应用,能够列出关于的方程是解决问题的关键. 8. 【解析】 【分析】 根据已知条件可先用含的式子表示出点的坐标、点的坐标,再利用其坐标表示出两个直角三角形的直角边长,然后即可表示出它们的面积,最后根据面积关系,列出关于的方程,解方程即可得解. 【详解】 解:∵, ∴ ∵四边形是正方形,点、点是反比例函数与正方形两边的交点 ∴设点的坐标为,点的坐标为 ∴, ∵ ∴ ∴. 故答案是: 【点睛】 本题考查了正方形的性质、反比例函数图像上点的坐标、坐标平面内两点间的距离、直角三角形的面积公式等知识点,列出关于的方程是解决问题的关键. 9. 【解析】 【分析】 根据题意添加适当的辅助线构造出直角三角形,利用等腰三角形的性质、翻折的性质即可求得答案. 【详解】 解:连接、、分别于点、的连线交于点、、,如图: 根据已知条件和翻折的性质可知 ∵是等腰直角三角形, ∴ ∵是面积为的等腰直角三角形,将沿向后折到的位置 ∴ ∴ ∴ ∴ ∴ ∴设, ∴都是等腰直角三角形 ∴ ∴ ∴ ∴ ∵由翻折的性质可得,由平行线的性质可得 ∴ ∴ ∴设, ∴ ∴ ∴ ∴ ∴ ∴ ∴ ∴ . 故答案是: 【点睛】 本题考查了翻折变换、等腰直角三角形的性质、勾股定理、锐角三角函数等知识,解题的关键是添加辅助线构造直角三角形从而解决问题,题目难度较大. 10.4. 【解析】 【分析】 【详解】 解:过A作AF⊥OB,作P作PG⊥OB, ∵△OAB与△ADC都为等边三角形, ∴∠BOA=∠DAC=60°, ∴AD∥OB, ∴AF=PG(平行线间的距离处处相等), ∵OB为△OBA和△OBP的底, ∴ ,即S△OBP=S△OAB(同底等高的三角形面积相等), 过B作BE⊥x轴,交x轴于点E,可得, ∵顶点B在双曲线y=(x>0)上,即k=4, ∴, 则. 故答案为:4. 11.180 【解析】 【分析】 作AD⊥CB,交CB的延长线于D点.在Rt△ACD中,利用∠CAD的正切函数求出邻边AD的长,进而可在Rt△ABD中,利用已知角的三角函数求出BD的长;由BC=CD﹣BD即可求出楼的高度. 【详解】 作AD⊥CB,交CB的延长线于D点. 则∠CDA=90°,∠CAD=60°,∠BAD=30°,CD=270. 在Rt△ACD中,tan∠CAD,∴AD90. 在Rt△ABD中,tan∠BAD,∴BD=AD•tan30°=9090,∴BC=CD﹣BD=270﹣90=180.则这栋大楼的高为180米. 故答案为180. 【点睛】 本题考查了俯角的定义,要求学生能借助俯角构造直角三角形并解直角三角形. 12.3+2. 【解析】 【分析】 设,则,利用折叠的性质得,,,则可判断四边形为正方形,所以,再根据折叠的性质得,则,然后根据勾股定理得到,再解方程求出即可. 【详解】 设,则, 把翻折,点落在边上的点处, ,,, 四边形为正方形, , 把翻折,点落在线段上的点处,折痕为,点在上, , , , 在中,, , 整理得,解得,(舍去), 即的长为. 故答案为:. 【点睛】 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,也考查了矩形的性质和勾股定理.查看更多