中考专题训练圆的切线的性质与判定

中考专题训练圆的切线的性质与判定

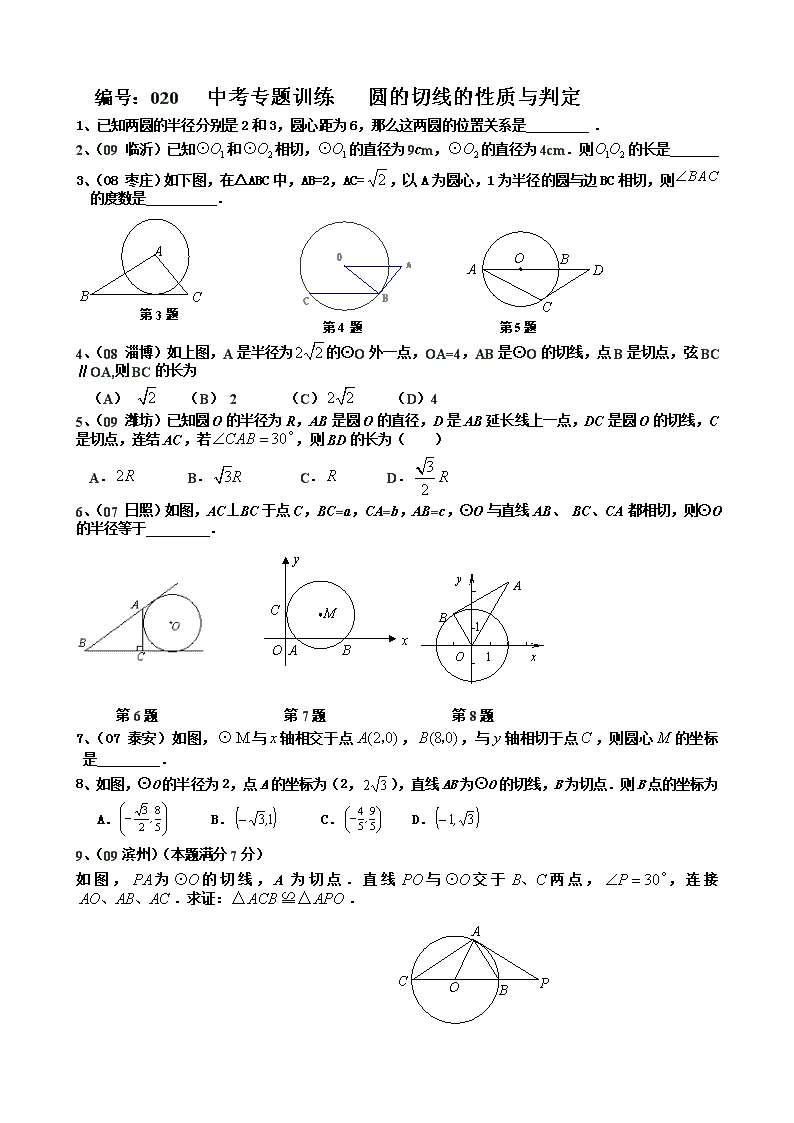
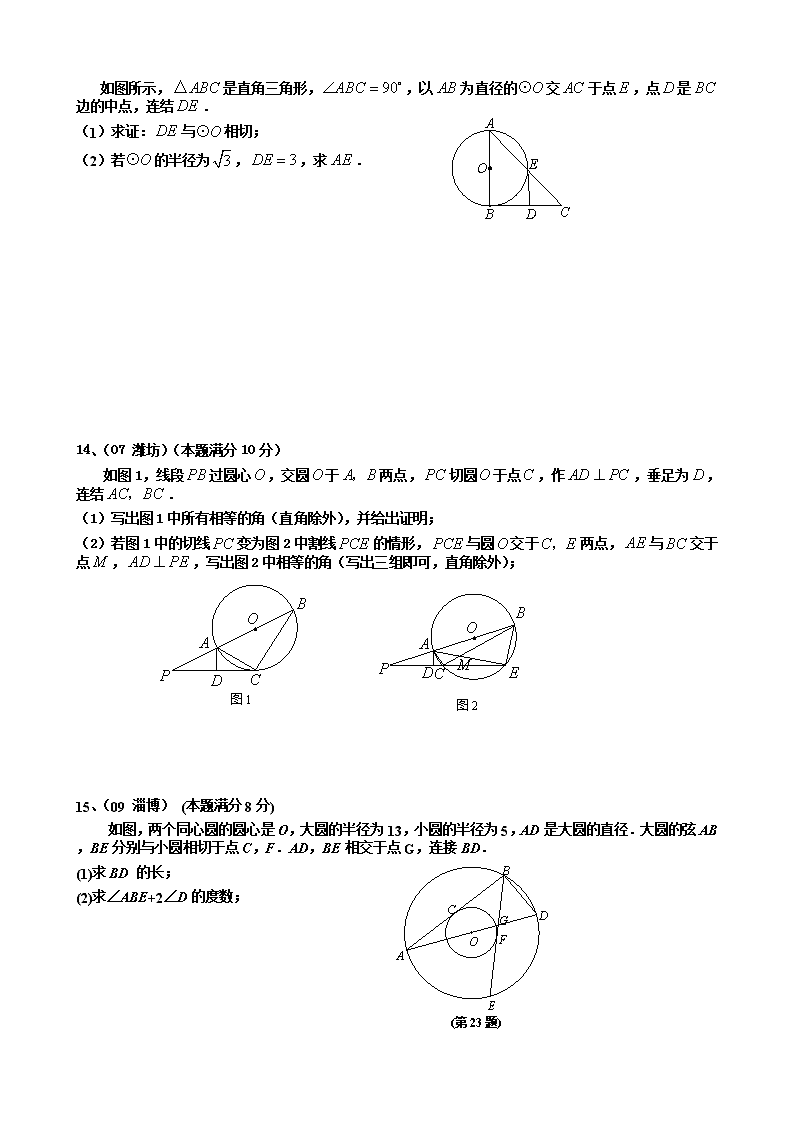
编号：020 中考专题训练 圆的切线的性质与判定 ‎1、已知两圆的半径分别是2和3，圆心距为6，那么这两圆的位置关系是 .‎ ‎2、（09 临沂）已知和相切，的直径为9cm，的直径为4cm．则的长是 ‎ 3、（08 枣庄）如下图，在△ABC中，AB=2，AC=，以A为圆心，1为半径的圆与边BC相切，则的度数是 ．‎ O B C D A A B C 第3题图 ‎ ‎ ‎ ‎ 第4 题 第5题 ‎ ‎4、（08 淄博）如上图，A是半径为的⊙O外一点，OA=4，AB是⊙O的切线，点B是切点，弦BC∥OA,则BC的长为 ‎（A） （B） 2 （C） （D）4 ‎ ‎5、（09 潍坊）已知圆O的半径为R，AB是圆O的直径，D是AB延长线上一点，DC是圆O的切线，C是切点，连结AC，若，则BD的长为（ ）‎ ‎ A． B． C． D．‎ ‎6、（07 日照）如图，AC⊥BC于点C，BC=a，CA=b，AB=c，⊙O与直线AB、 BC、CA都相切，则⊙O的半径等于 ． ‎ y x M B A O C x y O ‎1‎ ‎1‎ B A ‎ ‎ 第6题 第7题 第8题 ‎7、（07 泰安）如图，与轴相交于点，，与轴相切于点，则圆心的坐标是 ．‎ ‎8、如图，⊙O的半径为2，点A的坐标为（2，），直线AB为⊙O的切线，B为切点．则B点的坐标为 ‎ A．　　　B． C． D． ‎ ‎9、（09滨州）（本题满分7分）‎ 如图，为的切线，A为切点．直线与交于两点，，连接．求证：．‎ A O B P C A D B C E F G O ‎10、（09 聊城）(10分)如图，⊙O是△ABC的内切圆，与AB、BC、CA分别相切于点D、E、F，∠DEF＝45º．连接BO并延长交AC于点G，AB＝4，AG＝2 (1)求∠A的度数；(2)求⊙O的半径．‎ ‎11、（07 日照）如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E.‎ ‎（1）求证：点E是边BC的中点；‎ ‎（2）若EC=3，BD=，求⊙O的直径AC的长度；‎ （3）若以点O，D，E，C为顶点的四边形是正方形，试判断△ABC的形状，并说明理 编号：021‎ A G F E C B O ‎（第12题）‎ ‎12、（07 泰安）（本小题满分9分）‎ 如图，在中，，以为直径的圆交于点，交于点，过点作，垂足为．‎ ‎（1）求证：为的切线；‎ ‎（2）若过点且与平行的直线交的延长线于点，连结．当是等边三角形时，求的度数．‎ ‎13、（08 泰安）（本小题满分10分）‎ B D C E A O 如图所示，是直角三角形，，以为直径的交于点，点是边的中点，连结．‎ ‎（1）求证：与相切；‎ ‎（2）若的半径为，，求．‎ ‎ ‎ ‎14、（07 潍坊）（本题满分10分）‎ 如图1，线段过圆心，交圆于两点，切圆于点，作，垂足为，连结．‎ ‎（1）写出图1中所有相等的角（直角除外），并给出证明；‎ ‎（2）若图1中的切线变为图2中割线的情形，与圆交于两点，与交于点，，写出图2中相等的角（写出三组即可，直角除外）；‎ 图1‎ 图2‎ ‎15、（09 淄博） (本题满分8分)‎ A C B D G F E O ‎(第23题)‎ 如图，两个同心圆的圆心是O，大圆的半径为13，小圆的半径为5，AD是大圆的直径．大圆的弦AB，BE分别与小圆相切于点C，F．AD，BE相交于点G，连接BD．‎ ‎(1)求BD 的长；‎ ‎(2)求∠ABE+2∠D的度数；‎