高考数学最后冲刺经典大题预测大汇编
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
高考数学最后冲刺大题汇编(高分必备)
1. 三角函数
(1) 求值:主要考角的变换(配角,二倍角正逆两用,齐次式,角度相对性)
(2) 图像性质:降幂公式、辅助角公式、五点作图(方法)、四大性质、有范围的值域问题
(3) 正余弦定理:正余弦定理、面积公式(俩公式)、向量数量积、测量航海等实际应用问题
(4) 与二次函数、斜率、圆、椭圆参数方程相关的最值问题
2. 概率统计
(1) 几何概型:分清数轴和线性规划(坐标系)、积分(两种问题)有关问题
(2) 条件概率:根据条件叙述判断得到
(3) 古典概型
(4) 二项分布
3. 立体几何
(1) 线面平行垂直位置关系、空间角
(2) 体积、面积、三视图、斜二侧画法
4. 导数
(1) 两种切线问题:已知是切点;不是切点
(2) 两种单调性问题:求单调区间;已知单调性
(3) 与之相关的不等式证明、零点个数问题
5. 数列
(1) 相关思想
(2) 累加、累乘、错位相减、列项相消
(3) 数学归纳法
(4) 二项式定理
(5) 递推、同除、凑配等方法
(6) 等差等比数列相关公式
(7) 分段数列
(8) 函数相关
6. 解析几何
(1) 求轨迹:直接、转代、参数
(2) 几何性质
(3) 与判别式、韦达定理、面积、中点、弦长、最值(本身隐含,函数,均值)直线设法相关的问题
三角
1、已知函数的图象经过点和.
(1)求实数和的值;
(2)当为何值时,取得最大值.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
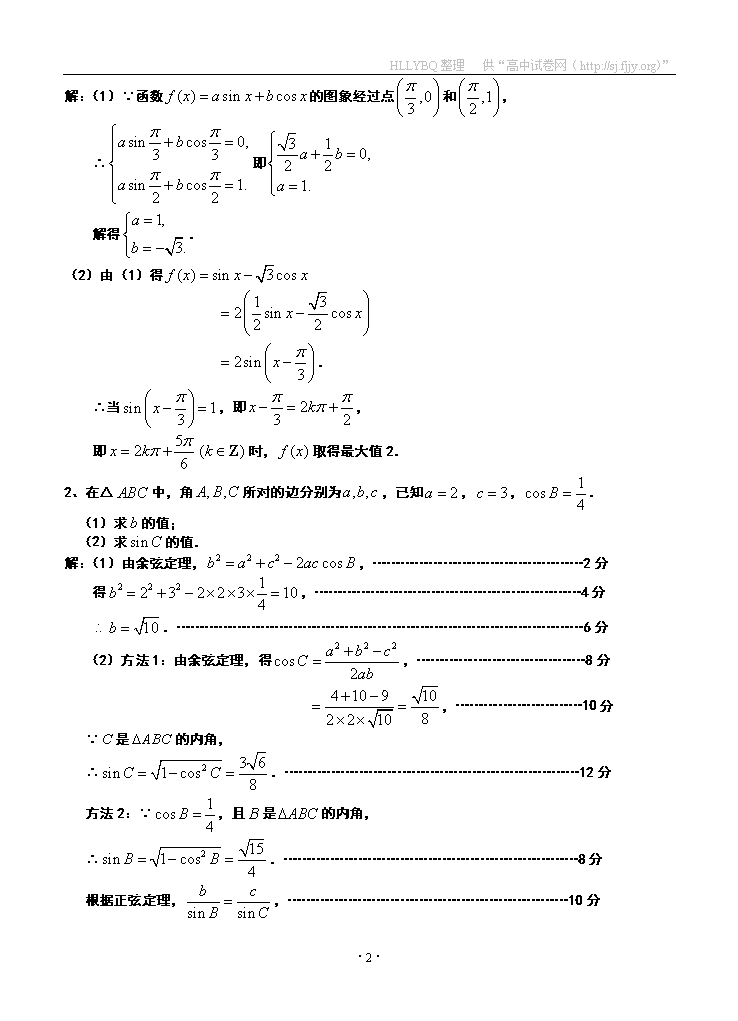
解:(1)∵函数的图象经过点和,
∴即
解得.
(2)由(1)得
.
∴当,即,
即时,取得最大值2.
2、在△中,角所对的边分别为,已知,,.
(1)求的值;
(2)求的值.
解:(1)由余弦定理,,………………………………………2分
得,…………………………………………………4分
.……………………………………………………………………………6分
(2)方法1:由余弦定理,得,………………………………8分
,………………………10分
∵是的内角,
∴.………………………………………………………12分
方法2:∵,且是的内角,
∴.………………………………………………………8分
根据正弦定理,,……………………………………………………10分
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
得. ……………………………………………12分
3、设函数.
(Ⅰ)求函数的最小正周期和单调递增区间;
(Ⅱ)当时,的最大值为2,求的值,并求出的对称轴方程.
解:(1) … 2分
则的最小正周期, ……………………………………………………………4分
且当时单调递增.
即为的单调递增区间(写成开区间不扣分).………………6分
(2)当时,当,即时.
所以. …………………………………………………9分
为的对称轴. ………………………………12分
4、已知,
(Ⅰ)求函数的最小正周期;
(Ⅱ) 当,求函数的零点.
解:(Ⅰ)=…………………….4分
故…………………………………………………5分
(Ⅱ)令,=0,又 …… ………….7分
…………………………………………9分
故 函数的零点是 ……………. 12分
5、已知函数
(Ⅰ)求函数f (x)的最小正周期;
(Ⅱ)求函数f (x)的单调减区间.
(Ⅰ)………………………………3分
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
所以 ………………………………6分
(Ⅱ)由(),……………………..9分
得()…………………………………….11分
所以,减区间为()………………………………12分
6、已知向量,,函数.
(Ⅰ)求的最大值及相应的的值;
(Ⅱ)若,求的值.
解:(Ⅰ)因为,,所以
.
因此,当,即()时,取得最大值;
(Ⅱ)由及得,两边平方得
,即.
因此,.
7、在△ABC中,角A、B、C所对边分别为a,b,c,已知,且最长边的边长为l.求:
(I)角C的大小;
(II)△ABC最短边的长.
解:(I)tanC=tan[π-(A+B)]=-tan(A+B)
∵, ∴ ……………………5分
(II)∵0
0,ω>0,x∈R)在一个周期内的图象如图所示,求直线y=与函数f(x)图象的所有交点的坐标。
解析:根据图象得A=2,T=π-(-)=4π,
∴ω=,∴y=2sin(+),
又由图象可得相位移为-,∴-=-,∴=.即y=2sin(x+)。
根据条件=2sin(),∴=2kπ+(k∈Z)或=2kπ+π(k∈Z),
∴x=4kπ+(k∈Z)或x=4kπ+π(k∈Z)。
∴所有交点坐标为(4kπ+)或(4kπ+)(k∈Z)。
10、若。
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
分析:注意的两变换,就有以下的两种解法。
解法一:由,
解法二:,
11、设函数f(x)=cos2x +sinx cosx+a(其中>0,aR),且f(x)的图象在y轴右侧的第一个高点的横坐标为。
(Ⅰ)求ω的值;
(Ⅱ)如果f(x)在区间上的最小值为,求a的值。
解析:(I)
依题意得 .
(II)由(I)知,。
又当时,,故,从而在区间
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
上的最小值为,故
12、已知向量
(I)若求 (II)求的最大值。
解析:(1);
当=1时有最大值,此时,最大值为。
13、在中,,,,求的值和的面积。
解法一:先解三角方程,求出角A的值。
又,
,
。
解法二:由计算它的对偶关系式的值。
①
,
②
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
① + ② 得 。
① - ② 得 。
从而 。
以下解法略去。
14、已知ΔABC的三个内角A、B.C成等差数列,其外接圆半径为1,且有。(1)求A、B.C的大小;(2)求ΔABC的的面积。
解析:∵A+B+C=180°且2B=A+C,∴B=60°,A+C=120°,C=120°-A。
∵,
∴=,
又∵0° 550(元)
答:乙商店的期望利润较大。
9、袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用表示取球终止所需要的取球次数.
(1)求袋中所有的白球的个数;
(2)求随机变量的概率分布;
(3)求甲取到白球的概率.
解:解:(1)设袋中原有个白球,由题意知
可得或(舍去)即袋中原有3个白球.
(2)由题意,的可能取值为1,2,3,4,5
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
所以的分布列为:
1
2
3
4
5
(3)因为甲先取,所以甲只有可能在第一次,第三次和第5次取球,记”甲取到白球”为事件,则.
10、随机地向半圆(为正常数)内掷一点,点落在园内任何区域的概率与区域的面积成正比,求原点与该点的连线与轴的夹角小于的概率.
0yx
yx
a
x
解析:半圆域如图
设‘原点与该点连线与轴夹角小于’
由几何概率的定义
。
1y
y
1y
0.9
0.1
0y
A
S
y
11、随机地取两个正数和,这两个数中的每一个都不超过1,试求与之和不超过1,积不小于0.09的概率.
解析:,不等式确定平面域。
‘’则发生的充要条件为不
等式确定了的子域,
故:
12、盒中装着标有数字1,2,3,4的卡片各2张,从盒中任意任取3张,每张卡片被抽出的可能性都相等,求:
(Ⅰ)抽出的3张卡片上最大的数字是4的概率;
(Ⅱ)抽出的3张中有2张卡片上的数字是3的概念;
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
(Ⅲ)抽出的3张卡片上的数字互不相同的概率。
解析:(I)“抽出的3张卡片上最大的数字是4”的事件记为A,
由题意得:;
(II)“抽出的3张中有2张卡片上的数字是3”的事件记为B,
则;
(III)“抽出的3张卡片上的数字互不相同”的事件记为C,“抽出的3张卡片上有两个数字相同”的事件记为D,由题意,C与D是对立事件,
因为,
所以.
13、为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列的前四项,后6组的频数从左到右依次是等差数列的前六项.
(Ⅰ)求等比数列的通项公式;
(Ⅱ)求等差数列的通项公式;
视力
4.3 4.4
4.5
4.6
4.7
4.8
4.9
5.0
5.1
5.2
0.1
0.3
(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率的大小.
解:(I)由题意知:,
∵数列是等比数列,∴公比
∴ .
(II) ∵=13,
∴,
∵数列是等差数列,∴设数列公差为,则得,
∴=87,
,,
(III)=,
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
(或=)
答:估计该校新生近视率为91%.
14、旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的期望.
解:(1)3个旅游团选择3条不同线路的概率为:P1=
(2)恰有两条线路没有被选择的概率为:P2=
(3)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3
P(ξ=0)= P(ξ=1)=
P(ξ=2)= P(ξ=3)=
∴ξ的分布列为:
ξ
0
1
2
3
P
∴期望Eξ=0×+1×+2×+3×=
15、在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球.求:(1)最多取两次就结束的概率;
(2)整个过程中恰好取到2个白球的概率; (3)取球次数的分布列和数学期望.
解析:(1)设取球次数为ξ,则
.
所以最多取两次的概率 ……………………4分
(2)由题意知可以如下取球:红白白、白红白、白白红、白白蓝四种情况,所以恰有两次取到白球的概率为 ……………………8分
(3)设取球次数为η,则
,则分布列为
η
1
2
3
P
取球次数的数学期望为
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
16、在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球.
求:(1)最多取两次就结束的概率;
(2)整个过程中恰好取到2个白球的概率;
(3)取球次数的分布列和数学期望.
解析:(1)设取球次数为ξ,则
.
所以最多取两次的概率 ……………………4分
(2)由题意知可以如下取球:红白白、白红白、白白红、白白蓝四种情况,所以恰有两次取到白球的概率为 ……………………8分
(3)设取球次数为η,则
,则分布列为
η
1
2
3
P
取球次数的数学期望为
17、某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中2题的便可提高通过. 已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是,且每题正确完成与否互不影响. 求:
(1) 分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
解:(1)设考生甲、乙正确完成实验操作的题数分别为、,
则取值分别为1,2,3;取值分别为0,1,2,3。…………………………………2分
,,。
∴考生甲正确完成题数的概率分布列为
1
2
3
。……………………………………………………………5分
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
∵,
同理:,,。
∴考生乙正确完成题数的概率分布列为:
0
1
2
3
………………………8分
。……………………………………………9分
(2)∵,
。
(或)。∴。
∵,,
∴。
从做对题数的数学期望考察,两人水平相当;从做对题数的方差考察,甲较稳定;从至少完成2题的概率考察,甲获得通过的可能性大。因此可以判断甲的实验操作能力较强。
说明:只根据数学期望与方差得出结论,也给分。
18、某工厂在试验阶段大量生产一种零件。这种零件有、两项技术指标需要检测,设各项技术指标达标与否互不影响。若有且仅有一项技术指标达标的概率为,至少一项技术指标达标的概率为.按质量检验规定:两项技术指标都达标的零件为合格品.
(Ⅰ)求一个零件经过检测为合格品的概率是多少?
(Ⅱ)任意依次抽出5个零件进行检测,求其中至多3个零件是合格品的概率是多少?
(Ⅲ)任意依次抽取该种零件4个,设表示其中合格品的个数,求与.
解:(Ⅰ)设、两项技术指标达标的概率分别为、
由题意得: …………3分
解得:或,∴.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
即,一个零件经过检测为合格品的概率为. …………6分
(Ⅱ)任意抽出5个零件进行检查,其中至多3个零件是合格品的概率为
………………10分
(Ⅲ)依题意知~B(4,),,
19、某市举行的一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
版本
人教A版
人教B版
性别
男教师
女教师
男教师
女教师
人数
6
3
4
2
(Ⅰ)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(Ⅱ)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为,求随机变量的分布列和数学期望.
解:(Ⅰ)从15名教师中随机选出2名共种选法, …………………………2分
所以这2人恰好是教不同版本的男教师的概率是. …………………5分
(Ⅱ)由题意得
; ;
.………………………………………………………………9分
故的分布列为
0
1
2
所以,数学期望.
20、已知暗箱中开始有3个红球,2个白裘。现每次从暗箱中取出一个球后,再将此球以及与它同色的5个球(共6个球)一起放回箱中。
(1)求第二次取出红球的概率;
(2)求第三次取出白球的概率;
(3)设取出白球得5分,取出红球得8分,求连续取球3次得分的期望值。
解:设第n次取出白球的概率为Pn,Qn
(1)第二次取出红球的概率是
…………………………………………4分
(2)三次取的过程共有以下情况:
白白白,白红白,红白白,红红白
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
所以第三次取出白球的概率是
…………………………………8分
(3)连续取球3次,得分的情况共有8种
5+5+5,8+5+5,5+8+5,5+5+8,8+8+5,8+5+8,5+8+8,8+8+8
∴
21、食品监管部门要对某品牌食品四项质量指标在进入市场前进行严格的检测,并规定四项指标中只要第四项不合格或其它三项指标中只要有两项不合格,这种品牌的食品就不能上市。巳知每项指标检测是相互独立的。若第四项不合格的概率为,且其它三项指标出现不合格的概率均是
(1)求该品牌的食品能上市的概率;
(2)生产厂方规定:若四项指标均合格,每位职工可得质量保证奖1500元;若第一、第二、第三项指标中仅有一项不合格且第四项指标合格,每位职工可得质量保证奖500元;若该品牌的食品不能上市,每位职工将被扣除质量保证金1000元。设随机变量表示某位职工所得质量保证奖金数,求的期望。
解:(1)该品牌的食品能上市的概率等于1减去该品牌的食品不能上市的概率,
即 6分
解法二:该品牌的食品能上市的概率等于四项指标都合格或第一、第二、第三项指标中仅有一项不合格且第四项指标合格的概率,即
(2);
易知 12分
∴的分布列为:
1500
500
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
∴的期望为
22、高考数学试题中共有10道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的.评分标准规定:“每题只选1项,答对得5分,不答或答错得0分.” 某考生每道题都给出了一个答案,已确定有6道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(Ⅰ)得50分的概率;
(Ⅱ)得多少分的可能性最大;
(Ⅲ)所得分数的数学期望.
解:(1)得分为50分,10道题必须全做对.
在其余的四道题中,有两道题答对的概率为,有一道题答对的概率为,还有一道答对的概率为,所以得分为50分的概率为:P= ………(3分)
(2)依题意,该考生得分的范围为{30,35,40,45,50}.
得分为30分表示只做对了6道题,其余各题都做错,所以概率为:
同样可以求得得分为35分的概率为:
得分为40分的概率为:; 得分为45分的概率为:;
得分为50分的概率为:
所以得35分或得40分的可能性最大. ………………(8分)
(3)由(2)可知的分布列为:
30
35
40
45
50
P
………(12分)
23、一个口袋中装有个红球(且)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(Ⅰ)试用表示一次摸奖中奖的概率;
(Ⅱ)若,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(Ⅲ)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为.当取多少时,最大?
解:(Ⅰ)一次摸奖从个球中任选两个,有种,
它们等可能,其中两球不同色有种,………………………2分
一次摸奖中奖的概率.………………………4分
(Ⅱ)若,一次摸奖中奖的概率,………………………6分
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
三次摸奖是独立重复试验,三次摸奖(每次摸奖后放回)恰有一次中奖的概率是
. ………………………8分
(Ⅲ)设每次摸奖中奖的概率为,则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为
,, ……………………10分
,知在上为增函数,在上为减函数,当时取得最大值.又,解得.……12分
答:当时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.
24、如图是两个独立的转盘,在两个图中三个扇形区域的圆心角分别为。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘指针所对的区域数为,转盘指针所对的区域为,,设的值为,每一次游戏得到奖励分为
⑴求且的概率;
⑵某人进行了次游戏,求他平均可以得到的奖励分
(注:这是一个几何概率题,几何概率的基本思想是把事件与几何区域对应,利用几何区域的度量来计算事件发生的概率,即事件的概率)
解:⑴由几何概率模型可知:;
则,
所以
⑵由条件可知的取值为:,则的分布列为:
他平均一次得到的奖励分即为的期望值:
所以给他玩次,平均可以得到分
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
25、旅游公司为3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团任选其中一条.
(Ⅰ)求3个旅游团选择3条不同线路的概率P1;
(Ⅱ)求恰有2条线路没有被选择的概率P2;
(Ⅲ)求选择甲线路的旅游团数x的分布列与数学期望.
解:(Ⅰ); …………………3分
(Ⅱ); …………………12分
(Ⅲ)x的取值为0、1、2、3.
,.
∴x的分布列为:
x
0
1
2
3
P
∴Ex=. …………………12分
26、在一次语文测试中,有一道我国四大文学名著《水浒传》、《三国演义》、《西游记》、《红楼梦》与它们的作者的连线题,已知连对一个得2分,连错一个不得分.
(Ⅰ)求该同学得分的分布列;
(Ⅱ)求该同学得分的数学期望.
解:(I)设该同学连对线的个数为y,得分为ξ,则y=0,1,2,4
∴ξ=0,2,4,8……………1分
……………3分
……………5分
……………7分
…………………9分
则ξ的分布列为
ξ
0
2
4
8
P
……………………10分
(II)Eξ=0×+2×+4×+8×=2
答:该人得分的期望为2分…………………12分
数列
1、已知数列中,且(且).
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
(1)若数列为等差数列,求实数的值;
(2)求数列的前项和.
解:(1)方法1:∵,
∴,.
设,由为等差数列,则有.
∴.
∴.
解得 .
事实上,
,
综上可知,当时,数列为首项是、公差是1的等差数列.
方法2:∵数列为等差数列,
设,由为等差数列,则有().
∴.
∴
.
综上可知,当时,数列为首项是、公差是1的等差数列.
(2)由(1)知,,
∴.
∴.
即.
令, ①
则. ②
②-①,得
.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
∴.
2、已知数列中,,,其前项和满足
(,).
(1)求数列的通项公式;
(2)设为非零整数,),试确定的值,使得对任意,都有成立.
解:(1)由已知,(,), …………………2分
即(,),且.
∴数列是以为首项,公差为1的等差数列.
∴.……………………………………………………………………………4分
(2)∵,∴,要使恒成立,
∴恒成立,
∴恒成立,
∴恒成立.……………………………………………………………6分
(ⅰ)当为奇数时,即恒成立,…………………………………………7分
当且仅当时,有最小值为1,
∴.………………………………………………………………………………9分
(ⅱ)当为偶数时,即恒成立,………………………………………10分
当且仅当时,有最大值,
∴.……………………………………………………………………………12分
即,又为非零整数,则.
综上所述,存在,使得对任意,都有.…………………14分
3、已知数列中,,且
(Ⅰ)求证:;
(Ⅱ)设,是数列的前项和,求的解析式;
(Ⅲ)求证:不等式对恒成立.
.解:
故,.……………………………………1分
又因为
则,即.………………………3分
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
所以, ……………………………………4
(2)
= ……………………………………6
因为=
所以,当时, ……………………………7
当时,……….(1)
得……(2)
=
……………………………9
综上所述: ……………………………10
(3)因为
又,易验证当,3时不等式不成立; ……………………………11
假设,不等式成立,即
两边乘以3得:
又因为
所以
即时不等式成立.故不等式恒成立. ……………………………14
4、设函数的定义域为R,当x<0时>1,且对任意的实数x,y∈R,有
(Ⅰ)求,判断并证明函数的单调性;
(Ⅱ)数列满足,且
①求通项公式。
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
②当时,不等式对不小于2的正整数恒成立,求x的取值范围。
解:(Ⅰ)时,f(x)>1
令x=-1,y=0则f(-1)=f(-1)f(0)∵f(-1)>1
∴f(0)=1……………………………2′
若x>0,则f(x-x)=f(0)=f(x)f(-x)故
故x∈R f(x)>0…………………………………………………4分
任取x1<x2
故f(x)在R上减函数………………………………………..6分
(Ⅱ)① 由f(x)单调性
………………………………………………………………………………8分
an+1=an+2 故{an}等差数列 ……………………………9分
②
是递增数列
………………………………………………………………………11分
当n≥2时,
……………………………12分
即
而a>1,∴x>1
故x的取值范围(1,+∞)……………………………14分
5、如图,、、…、()是曲线:()上的个点,点()在轴的正半轴上,且是正三角形(是坐标原点).
(Ⅰ)写出、、;
(Ⅱ)求出点()的横坐标关于的表达式;
(Ⅲ)设,若对任意的正整数,当时,不等式恒成立,求实数的取值范围.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
解:(Ⅰ),,;
(Ⅱ)依题意,得,,由此及得
,
即.
由(Ⅰ)可猜想:().
下面用数学归纳法予以证明:
(1)当时,命题显然成立;
(2)假定当时命题成立,即有,则当时,由归纳假设及
得,即
,
解之得(不合题意,舍去),
即当时,命题成立.
由(1)、(2)知:命题成立.
(Ⅲ)
.
令(),则,所以在上是增函数,故当时,取得最小值,即当时,.
(,)
,即()
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
.解之得,实数的取值范围为.
6、已知数列{ an }的前n项和Sn满足,Sn=2an+(—1)n,n≥1。
①求数列{ an }的通项公式;
②求证:对任意整数m>4,有
解:解(1)化简即
即 由a1=1,故数列{}
是以为首项,公比为2的等比数列。
故即
(2)由已知得
故
7、直线过(1,0)点,且关于直线y=x对称的直线为,已知点在上,。当n≥2时,有
(1)求的方程;
(2)求{ an}的通项公式;
(3)设求数列{ bn}的前n项和Sn
解:(1)由 设
设: 又(1,0)关于 对称点
为(0,1)在上,所以1=0+b,b=1 所以:
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
(2)因为 所以
(3)所以
8、已知等差数列{ an}的第2项a2=5,前10项之和S10=120,若从数列{ an}中,依次取出第2项,第4项,第8项,…,第2n项,按原来的顺序组成一个新数列{bn},设{bn}的前n项和为Tn,试比较Tn+1与2Tn的大小。
解:由a1+d=5,10a1+45d=120 得a1=3,d=2
所以an=2n+1,bn=a2n=2n+1+1
所以,
当n>5时,,当n=5时,
,当n<5时,
9、已知数列中,
(1)求证:数列与都是等比数列;(2)求数列前的和;
(3)若数列前的和为,不等式对恒成立,求的最大值。
解:(1)∵,∴ 2分
∴数列是以1为首项,为公比的等比数列;
数列是以为首项,为公比的等比数列。 4分
(2)
9分
(3)
当且仅当时取等号,所以,即,∴的最大值为-48
10、已知等差数列的公差大于0,且是方程的两根,数列的前n项的和为,且.
(1) 求数列,的通项公式;
(2) 记,求证:.
解:(Ⅰ)∵a3,a5是方程的两根,且数列的公差d>0,
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
∴a3=5,a5=9,公差
∴ ………………3分
又当n=1时,有b1=S1=1-
当
∴数列{bn}是等比数列,
∴ …………6分
(Ⅱ)由(Ⅰ)知 …………9分
∴
∴ …………………………12分
11、已知数列的前项和为,对一切正整数,点都在函数的图像上,且过点的切线的斜率为.
(1)求数列的通项公式.
(2)若,求数列的前项和.
(3)设,等差数列的任一项,其中是中的最小数,,求的通项公式.
解:(1)点都在函数的图像上,,
当时,
当n=1时,满足上式,所以数列的通项公式为…….3分
(2)由求导可得
过点的切线的斜率为,.
.
①
由①×4,得
②
①-②得:
………………………………………………………………..7分
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
(3),.
又,其中是中的最小数,.
是公差是4的倍数,.
又,,解得m=27.
所以,
设等差数列的公差为,则
,所以的通项公式为…………12分
12、函数对任意x∈R都有f(x)+f(1-x)=.
(1)求的值;
(2)数列的通项公式。
(3)令试比较Tn与Sn的大小。
解:(1)令
令
(2)
又,两式相加
是等差数列
(3)
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
13、已知数列中,其前n项和为 满足.
(1)试求数列的通项公式.
(2)令是数列的前n项和,证明:.
(3)证明:对任意的,均存在,使得(2)中的成立.
解:(1)由得
,,即
又,
故数列的通项公式为.……………………(4分)
(2)
……………………(8分)
(3)证明:由(2)可知
若,则得,化简得
,
当,即………(10分)
当,即
,取即可,
综上可知,对任意的均存在使得时(2)中的成立(12分)
14、已知数列的前n项和为,点在曲线
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
上且.
(1)求数列的通项公式;
(2)数列的前n项和为且满足,设定的值使得数列是等差数列;
解:(1)
∴∴
∴数列是等差数列,首项公差d=4
∴ ∴∵
∴…………(4分)
(2)由
得
∴∴
∴
若为等差数列,则
∴
导数
1、已知,.
(1)当时,求证:在上是减函数;
(2)如果对不等式恒成立,求实数的取值范围.
解:(1)当时,,
∵,∴在上是减函数.
(2)∵不等式恒成立,即不等式恒成立,
∴不等式恒成立. 当时, 不恒成立;
当时,不等式恒成立,即,∴.
当时,不等式不恒成立. 综上,的取值范围是.
2、设函数.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
(1)求函数的单调递增区间;
(2)若关于的方程在区间内恰有两个相异的实根,求实数的取值范围.
解:(1)函数的定义域为,…………………………………………………1分
∵,………………………………………2分
∵,则使的的取值范围为,
故函数的单调递增区间为. ……………………………………………4分
(2)方法1:∵,
∴.…………………………6分
令,
∵,且,
由.
∴在区间内单调递减,在区间内单调递增,……………………9分
故在区间内恰有两个相异实根……12分
即解得:.
综上所述,的取值范围是.………………………………14分
方法2:∵,
∴.…………………………6分
即,
令,
∵,且,
由.
∴在区间内单调递增,在区间内单调递减.……………………9分
∵,,,
又,
故在区间内恰有两个相异实根.
……………………………………12分
即.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
综上所述,的取值范围是. ……………………………14分
3、已知函数(其中) ,
点从左到右依次是函数图象上三点,且.
(Ⅰ) 证明: 函数在上是减函数;
(Ⅱ) 求证:⊿是钝角三角形;
(Ⅲ) 试问,⊿能否是等腰三角形?若能,求⊿面积的最大值;若不能,请说明理由.
解:(Ⅰ)
…………………………
所以函数在上是单调减函数. …………………………4分
(Ⅱ) 证明:据题意且x1f (x2)>f (x3), x2=…………………………6分
…………………8分
即⊿是钝角三角形……………………………………..9分
(Ⅲ)假设⊿为等腰三角形,则只能是
即
① …………………………………………..12分
而事实上, ②
由于,故(2)式等号不成立.这与式矛盾. 所以⊿不可能为等腰三角形..14分
4、已知,(),直线与函数、的图像都相切,且与函数的图像的切点的横坐标为1.
(Ⅰ)求直线的方程及的值;
(Ⅱ)若(其中是的导函数),求函数的最大值;
(Ⅲ)当时,求证:.
解:(Ⅰ)依题意知:直线是函数在点处的切线,故其斜率
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
,
所以直线的方程为.
又因为直线与的图像相切,所以由
,
得(不合题意,舍去);
(Ⅱ)因为(),所以
.
当时,;当时,.
因此,在上单调递增,在上单调递减.
因此,当时,取得最大值;
(Ⅲ)当时,.由(Ⅱ)知:当时,,即.因此,有
.
5、已知,,.
(1)当a=1时,求的单调区间;
(2)求过点的切线与直线及曲线所围成的封闭图形的面积;
(3)是否存在实数a,使的极大值为3?若存在,求出a的值,若不存在,请说明理由.
解:(1)当. ……(1分)
……(3分)
∴的单调递增区间为(0,1),单调递减区间为:,. ……(4分)
(2)切线的斜率为, ∴ 切线方程为. ……(6分)
所求封闭图形面积为
. ……(8分)
(3), ……(9分)
令. ……(10分)
列表如下:
x
(-∞,0)
0
(0,2-a)
2-a
(2-a,+ ∞)
-
0
+
0
-
↘
极小
↗
极大
↘
由表可知,. ……(12分)
设,∴上是增函数,……(13分)
∴ ,即,
∴不存在实数a,使极大值为3. ……(14分)
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
6、已知函数。(Ⅰ)设,讨论的单调性;(Ⅱ)若对任意恒有,求的取值范围。
解:(Ⅰ)f(x)的定义域为(-∞,1)∪(1,+∞).对f(x)求导数得 f '(x)= e-ax。
(ⅰ)当a=2时, f '(x)= e-2x, f '(x)在(-∞,0), (0,1)和(1,+ ∞)均大于0, 所以f(x)在(-∞,1), (1,+∞).为增函数;
(ⅱ)当00, f(x)在(-∞,1), (1,+∞)为增函数.;
(ⅲ)当a>2时, 0<<1, 令f '(x)=0 ,解得x1= - , x2= ;
当x变化时, f '(x)和f(x)的变化情况如下表:
x
(-∞, -)
(-,)
(,1)
(1,+∞)
f '(x)
+
-
+
+
f(x)
↗
↘
↗
↗
f(x)在(-∞, -), (,1), (1,+∞)为增函数, f(x)在(-,)为减函数。
(Ⅱ)(ⅰ)当0f(0)=1;
(ⅱ)当a>2时, 取x0= ∈(0,1),则由(Ⅰ)知 f(x0)1且e-ax≥1,
得:f(x)= e-ax≥ >1. 综上当且仅当a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1。
7、已知函数f(x)=x+ x,数列|x|(x>0)的第一项x=1,以后各项按如下方式取定:曲线x=f(x)在处的切线与经过(0,0)和(x,f (x))两点的直线平行(如图)求证:当n时,
(Ⅰ)x(Ⅱ)。
证明:(I)因为所以曲线在处的切线斜率
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
因为过和两点的直线斜率是所以.
(II)因为函数当时单调递增,而
,
所以,即因此
又因为令则
因为所以
因此 故
8、已知 ,其中.
(Ⅰ)求使在上是减函数的充要条件;
(Ⅱ)求在上的最大值;
(Ⅲ)解不等式.
解:(1). , 时,,即.
当时,, 即.
在上是减函数的充要条件为. ………(4分)
(2)由(1)知,当时为减函数,的最大值为;
当时,,当时,,当时,
即在上是增函数,在上是减函数,时取最大值,
最大值为, 即 …(13分)
(3)在(1)中取,即, 由(1)知在上是减函数.
,即,
,解得或.
故所求不等式的解集为[ ……………(8分)
9、已知函数,设。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以图象上任意一点为切点的切线的斜率 恒成立,求实数的最小值。
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
(Ⅲ)是否存在实数,使得函数的图象与的图象恰好有四个不同的交点?若存在,求出的取值范围,若不存在,说名理由。
解.(Ⅰ)
由。
(Ⅱ)
当
…………………………………………4分
(Ⅲ)若的图象与
的图象恰有四个不同交点,
即有四个不同的根,亦即
有四个不同的根。
令,
则。
当变化时的变化情况如下表:
(-1,0)
(0,1)
(1,)
的符号
+
-
+
-
的单调性
↗
↘
↗
↘
由表格知:。
画出草图和验证可知,当时,
………………12分
10、已知函数,求导函数,并确定的单调区间.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
解:
.
令,得.
当,即时,的变化情况如下表:
0
当,即时,的变化情况如下表:
0
所以,当时,函数在上单调递减,在上单调递增,
在上单调递减.
当时,函数在上单调递减,在上单调递增,在上单调递减.
当,即时,,所以函数在上单调递减,在上单调递减.
11、由原点O向三次曲线y=x3-3ax2+b x (a≠0)引切线,切于不同于点O的点P1(x1,y1),再由P1引此曲线的切线,切于不同于P1的点P2(x2,y2),如此继续地作下去,…,得到点列{Pn(xn,y n)},试回答下列问题:
(Ⅰ)求x1;
(Ⅱ)求x n与xn+1的关系;
(Ⅲ)若a>0,求证:当n为正偶数时,x na.
解:(Ⅰ)由f (x)=x3-3ax2+b x,①.得f ¢(x)=3x2-6ax+b.∴可设过曲线①上点P1(x1, y1)的切线l1的方程是:y-y1=f ¢(x1)(x-x1),即.∵l1过原点,∴.∴.∴.(Ⅱ)过曲线①上点Pn+1(xn+1,yn+1)的切线ln+1的方程是.由ln+1过曲线①上点P n(x n, yn),有.∵x n-xn+1≠0,消去xn-xn+1,得,
化简,得.再消去xn-xn+1,得xn+2xn+1-3a = 0.(Ⅲ)由(Ⅱ)得,∴.∴数列{xn-a}是以x1-a(=)为首项,公比为-的等比数列.∴,即.∵a>0,∴当n为正偶数时,=< a;当n为正奇数时,=> a.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
12、设曲线≥0)在点M(t,e--t)处的切线与x轴y轴所围成的三角形面积为S(t).
(Ⅰ)求切线的方程;
(Ⅱ)求S(t)的最大值.
解:(Ⅰ)因为所以切线的斜率为
故切线的方程为即.
(Ⅱ)令y=0得x=t+1,
又令x=0得
所以S(t)=
=
从而
∵当(0,1)时,>0,
当(1,+∞)时,<0,
所以S(t)的最大值为S(1)=
13、已知,函数设,记曲线在点处的切线为。
(Ⅰ)求的方程;
(Ⅱ)设与轴的交点为,证明:①②若,则
解:(1)的导数,由此得切线的方程
,
(2)依题得,切线方程中令,得
,其中,
(ⅰ)由,,有,及,
∴,当且仅当时,。
(ⅱ)当时,,因此,,且由(ⅰ),,
所以。
14、已知函数
(Ⅰ)若,求证:;
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
(Ⅱ)是否存在实数,使方程有四个不同的实根?若存在,求出的取值范围;若不存在,说明理由.
(文科做)设函数
⑴求函数的单调区间、极值.
⑵若当时,恒有,试确定a的取值范围..
理解:(I)令
则……(4分)
因 故函数上是增函数.又处连续,所以, 函数上是增函数.时,(7分)
(Ⅱ)令
……(9分)
当变化时,、的变化关系如下表:
-1
(-1,0)
0
(0,1)
1
(1,+)
-
0
+
0
-
0
+
极小值
极大值
0
极小值
据此可画出的简图如下,……(12分)
故存在,使原方程
有4个不同实根.……(14分)
文. 解:令由表
x
a
3a
f′
-
0
+
0
-
f
递减
递增
b
递减
可知:当时,函数为减函数,当时。函数也为减函数;当时,函数为增函数.
·70·
HLLYBQ整理 供“高中试卷网(http://sj.fjjy.org)”
当x=a时,的极小值为时,的极大值为b.
⑵由
∵0
查看更多