- 2021-04-12 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学高考题型历炼Word解析版72导数的简单应用与定积分
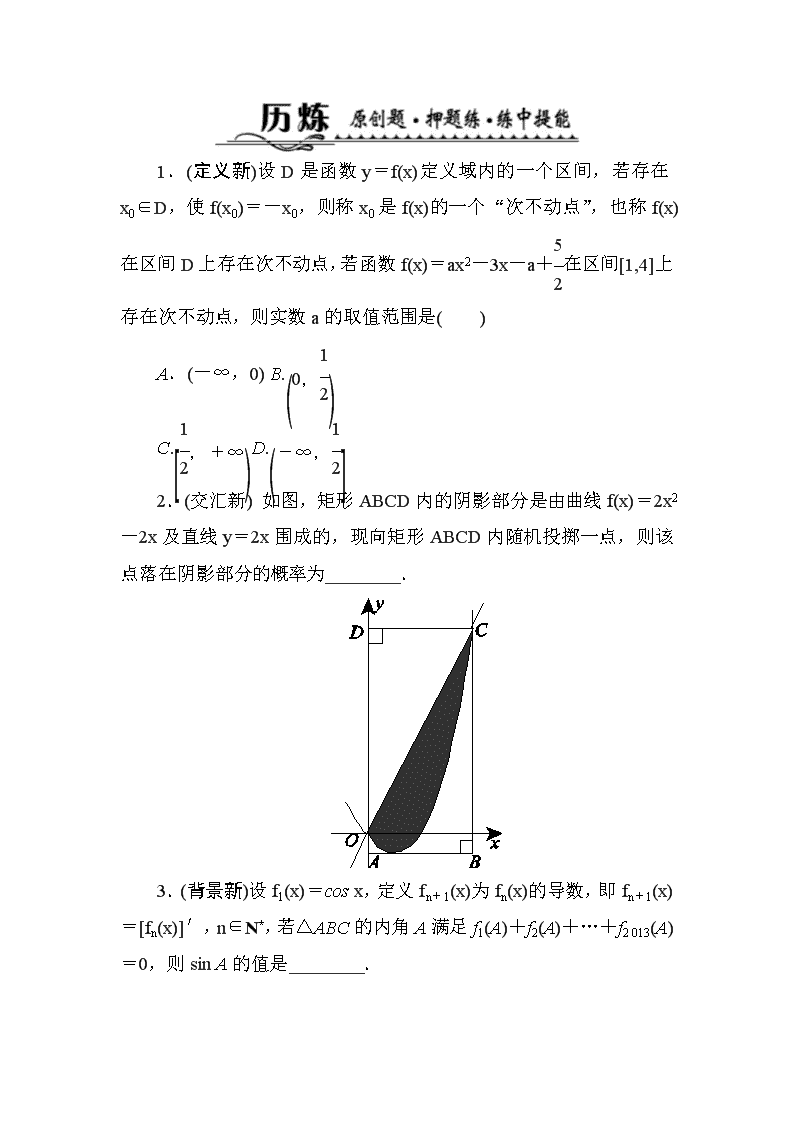
1.(定义新)设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使f(x0)=-x0,则称x0是f(x)的一个“次不动点”,也称f(x)在区间D上存在次不动点,若函数f(x)=ax2-3x-a+在区间[1,4]上存在次不动点,则实数a的取值范围是( ) A.(-∞,0) B. C.D. 2.(交汇新) 如图,矩形ABCD内的阴影部分是由曲线f(x)=2x2-2x及直线y=2x围成的,现向矩形ABCD内随机投掷一点,则该点落在阴影部分的概率为________. 3.(背景新)设f1(x)=cos x,定义fn+1(x)为fn(x)的导数,即fn+1(x)=[fn(x)]′,n∈N*,若△ABC的内角A满足f1(A)+f2(A)+…+f2 013(A)=0,则sin A的值是________. 4.(交汇新)已知函数f(x)=在x=0,x=处存在极值. (1)求实数a,b的值; (2)函数y=f(x)的图象上存在两点A,B,使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围; (3)当c=e时,讨论关于x的方程f(x)=kx(k∈R)的实根的个数. [历 炼] 1.解析:设g(x)=f(x)+x,依题意,存在x∈[1,4],使g(x)=f(x)+x=ax2-2x-a+=0.当x=1时,g(1)=≠0;当x≠1时,由ax2-2x-a+=0,得a=.记h(x)=(1<x≤4),则由h′(x)==0,得x=2或x=(舍去).当x∈(1,2)时,h′(x)>0;当x∈(2,4)时,h′(x)<0,即函数h(x)在(1,2)上是增函数,在(2,4)上是减函数,因此当x=2时,h(x)取得最大值,最大值是h(2)=,故满足题意的实数a的取值范围是.故选D. 答案:D 2.解析:曲线f(x)=2x2-2x与直线y=2x的交点为(0,0)和(2,4),曲线f(x)=2x2-2x与x轴的交点坐标为(0,0)和(1,0),其顶点坐标为.因为矩形ABCD的面积为×2=9,阴影部分的面积为(2x-2x2+2x)dx==,所以该点落在阴影部分的概率为=. 答案: 3.解析:∵f1(x)=cos x,∴f2(x)=[f1(x)]′=-sin x,f3(x)=[f2(x)]′=-cos x,f4(x)=[f3(x)]′=sin x,f5(x)=[f4(x)]′=cos x,…,∴fn(x)+fn+1(x)+fn+2(x)+fn+3(x)=0,∴f1(A)+f2(A)+…+f2 013(A)=f2 013(A)=f1(A)=cos A=0,又A为△ABC的内角.∴sin A=1. 答案:1 4.解析:(1)当x<1时,f′(x)=-3x2+2ax+b. 因为函数f(x)在x=0,x=处存在极值, 所以 解得a=1,b=0. (2)由(1)得f(x)= 根据条件知A,B的横坐标互为相反数,不妨设A(-t,t3+t2),B(t,f(t))(t>0). 若t<1,则f(t)=-t3+t2, 由∠AOB是直角,得·=0, 即-t2+(t3+t2)(-t3+t2)=0, 即t4-t2+1=0,此时无解; 若t≥1,则f(t)=c(et-1-1).由于AB的中点在y轴上,且∠AOB是直角,所以点B不可能在x轴上,即t≠1.同理·=0,即-t2+(t3+t2)·c(et-1-1)=0,则 c=. 因为函数y=(t+1)(et-1-1)在t>1上的值域是(0,+∞), 所以实数c的取值范围是(0,+∞). (3)由方程f(x)=kx, 知kx= 因为0一定是方程的根,所以以下仅就x≠0时进行研究. 方程等价于k= 构造函数g(x)=则 对于x<1且x≠0部分,函数g(x)=-x2+x的图象是开口向下的抛物线的一部分,当x=时取得最大值,其值域是(-∞,0)∪; 对于x≥1部分,函数g(x)=,由g′(x)=>0,知函数g(x)在[1,+∞)上单调递增且g(1)=0,则g(x)的值域为[0,+∞). 所以,x≠0时: ①当k>或k≤0时,方程f(x)=kx有一个实根; ②当k=时,方程f(x)=kx有两个实根; ③当0<k<时,方程f(x)=kx有三个实根.查看更多