2021版高考数学一轮复习第八章数列8-3等比数列课件理北师大版

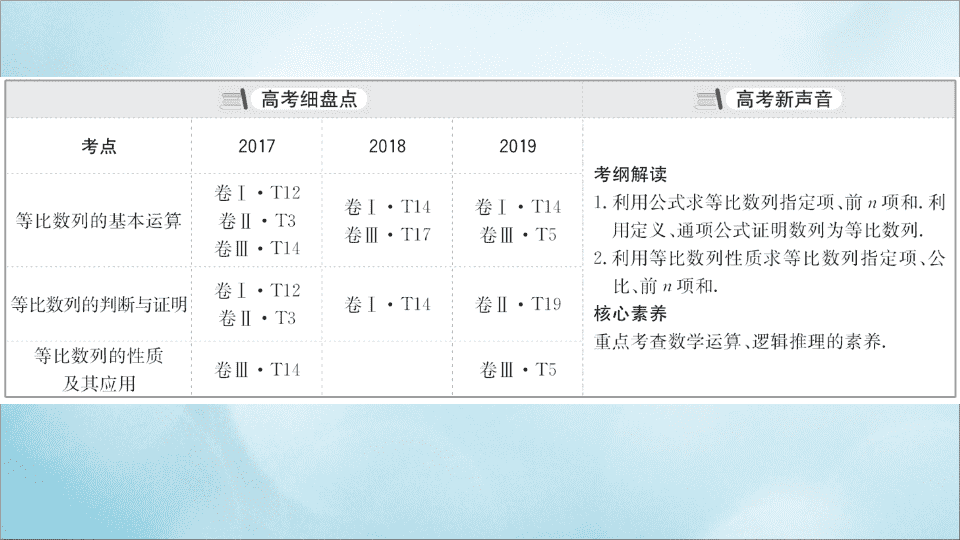
2021版高考数学一轮复习第八章数列8-3等比数列课件理北师大版

第三节　等 比 数 列 内容索引 必备知识 · 自主学习 核心考点 · 精准研析 核心素养 · 微专题 核心素养测评 【教材 · 知识梳理】 1. 等比数列与等比中项 (1) 等比数列的定义式 :________. (2) 等比中项 ① 定义 :a,G,b 成等比数列 , 则 G 叫做 a 和 b 的等比中项 . ② 公式 :a,G,b 成等比数列 ⇔_____. ③ 性质 :{a n } 是等比数列 ⇒ =_____ 或 =_______. G 2 =ab a n a n+2 a n-m a n+m 2. 等比数列的有关公式 (1) 通项公式 :a n =_____. (2) 前 n 项和公式 : a 1 q n-1 3. 等比数列的性质 (1) 通项公式的推广 :a n =a m ·____(n,m∈N * ). (2) 若 {a n } 为等比数列 , 且 k+ l =m+n(k, l ,m,n∈N * ), 则 a k ·a l =a m ·a n . (3) 若 {a n },{b n }( 项数相同 ) 是等比数列 , 则 {λa n }(λ≠0),{ },{ }, {a n ·b n },{ } 仍是等比数列 . (4) 在等比数列 {a n } 中 , 等距离取出若干项也构成一个等比数列 , 即 a n ,a n+k , a n+2k ,a n+3k ,… 为等比数列 , 公比为 __. q n-m q k (5) 若公比不为 -1 的等比数列 {a n } 的前 n 项和为 S n , 则 S n ,S 2n -S n ,S 3n -S 2n ,… 成等比数 列 , 其公比为 __. (6) 若 a 1 ·a 2 ·…·a n =T n , 则 T n , … 成等比数列 . q n 【知识点辨析】 ( 正确的打 “ √ ” , 错误的打 “ × ” ) (1) 等比数列 {a n } 的公比 q>1, 则该数列单调递增 . ( 　　 ) (2) 数列 {a n },{b n } 都是等比数列 , 则数列 {a n b n }, 仍然是等比数列 . ( 　　 ) (3) 数列 {a n } 的通项 a n =a n , 则其前 n 项和为 S n = ( 　　 ) (4) 设 S n 是等比数列 {a n } 的前 n 项和 , 则 S n ,S 2n -S n ,S 3n -S 2n 是等比数列 . ( 　　 ) 提示 : (1)×. 在等比数列 {a n } 中 , 若公比 q>1, 当 a 1 >0 时 , 该数列为递增数列 ,a 1 <0 时 , 该数列为递减数列 , 所以 (1) 错误 . (2)√. 设等比数列 {a n },{b n } 的公比分别为 q 1 ,q 2 , 则 =q 1 q 2 ( 与 n 无关的常 数 ), ( 与 n 无关的常数 ), 所以 (2) 正确 . (3)×. 对于数列 {a n }, 当 a=1 时 ,S n =n, 当 a≠1 时 , 则其前 n 项和为 S n = 所以 (3) 错误 . (4)×. 在公比 q=-1,n 为偶数时 ,S n =S 2n -S n =S 3n -S 2n =0, 此时 ,S n ,S 2n -S n ,S 3n -S 2n 不是等 比数列 , 所以 (4) 错误 . 【易错点索引】 序号 易错警示 典题索引 1 运算错误 考点一、 T5 2 q=1 的特殊性是否讨论 考点一、 T2 3 不能进行正确转化 考点二、 T2 4 等比数列性质应用错误 考点三、角度 1,2 【教材 · 基础自测】 1.( 必修 5P25T3 改编 )3+ 与 3- 的等比中项为 ________.   【解析】 因为 (3+ )×(3- )=3 2 -( ) 2 =4, 所以 3+ 与 3- 的等比中 项为 ±2. 答案 : ±2 2.( 必修 5P31B 组 T3 改编 ) 一个等比数列的前 n 项和为 12, 前 2n 项和为 36, 则前 3n 项和为 ________.  【解析】 因为 S n ,S 2n -S n ,S 3n -S 2n 成等比数列 , 所以 12,24,S 3n -36 成等比数列 , 所以 24 2 =12(S 3n -36), 解得 S 3n =84. 答案 : 84 3.( 必修 5P27 例 5 改编 ) 设 {a n } 是公比为正数的等比数列 , 若 a 1 =1,a 5 =16, 则数列 {a n } 的前 7 项和为 ________.  【解析】 设等比数列 {a n } 的公比为 q(q>0), 由 a 5 =a 1 q 4 =16,a 1 =1, 得 16=q 4 , 解得 q=2, 所以 S 7 = =127. 答案 : 127 【解题新思维】 　活用等比数列前 n 项和的性质解题　   　　　　　　　　　　　　　　　　　　　 【结论】 在等比数列 {a n } 中 , 其前 n 项和为 S n , 当公比 q≠-1 时 ,S n ,S 2n -S n ,S 3n -S 2n , … 成等比数列 (n∈N * ). 【典例】 设等比数列 {a n } 的前 n 项和为 S n , 若 =3, 则 =________.  【解析】 由等比数列的性质 S 3 ,S 6 -S 3 ,S 9 -S 6 仍成等比数列 , 由已知得 S 6 =3S 3 , 所以 即 S 9 -S 6 =4S 3 ,S 9 =7S 3 , 所以 . 答案 : 【一题多解】 因为 {a n } 为等比数列 , 由 =3, 设 S 6 =3a,S 3 =a(a≠0), 所以 S 3 , S 6 -S 3 ,S 9 -S 6 为等比数列 , 即 a,2a,S 9 -S 6 成等比数列 , 所以 S 9 -S 6 =4a, 解得 S 9 =7a, 所 以 答案 : 【迁移应用】 已知数列 {a n } 是等比数列 ,S n 为其前 n 项和 , 若 a 1 +a 2 +a 3 =4,a 4 +a 5 +a 6 =8, 则 S 12 = ( 　　 ) A.40 B.60 C.32 D.50 【解析】 选 B. 数列 S 3 ,S 6 -S 3 ,S 9 -S 6 ,S 12 -S 9 是等比数列 , 即数列 4,8,S 9 -S 6 ,S 12 -S 9 是首项为 4, 公比为 2 的等比数列 , 则 S 9 -S 6 =a 7 +a 8 +a 9 =16,S 12 -S 9 =a 10 +a 11 +a 12 =32, 因此 S 12 =4+8+16+32=60.