2019届初三数学中考复习 《圆》复习建议

2019届初三数学中考复习 《圆》复习建议

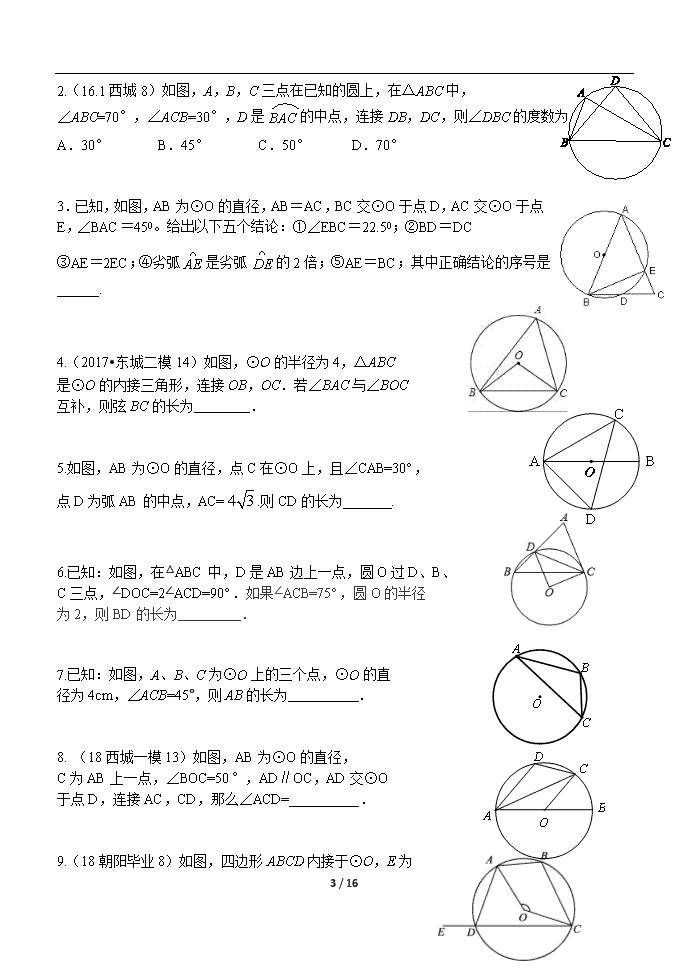
1 / 16 《圆》复习建议 一、2019 年中考说明 与 2018 年中考说明完全一致 考试内容 考试要求 A B C 图 形 与 几 何 图 形 的 性 质 圆的有关 概念 理解圆、弧、弦、圆心角、 圆周角的概念；了解等圆、 等弧的概念 能利用圆的有关概念解决有 关简单问题 圆的有关 性质 了解弧、弦、圆心角的关系， 理解圆周角与圆心角及其所 对弧的关系 能利用垂径定理解决有关简 单问题；能利用圆周角定理 及其推论解决有关简单问题 运用圆的性 质的有关内 容解决有关 问题 点和圆的 位置关系 了解点与圆的位置关系 尺规作图（利用基本作图完 成）：过不在同一直线上的三 点作圆；能利用点和圆的位 置关系解决有关简单问题 直线与圆 的位置关 系 了解直线与圆的位置关系； 会判 断直线 和圆 的位置 关 系；理解切线与过切点的半 径之间的关系；会用三角尺 过圆上一点画圆的切线 掌握切线的概念；能利用切 线的判定和性质解决有关简 单问题；能利用直线与圆的 位置关系解决简单问题；能 利用切线长定理解决有关简 单问题 运用圆的切 线的有关内 容解决有关 问题 多边形和 圆 了解圆内接多边形和多边形 外接圆的概念；了解三角形 外心的概念；知道三角形的 内切圆；了解三角形的内心； 了解正多边形的概念及正多 边形与圆的关系 能利用圆内接四边形的对角 互补解决有关简单问题；能 利用正多边形解决有关简单 问题；尺规作图（利用基本 作图完成）：作三角形外接 圆、内切圆，作圆的内接正 方形和正六边形 弧长、扇 形面积和 圆锥 会计 算圆的 弧长 和扇形 面 积； 会求圆锥的侧面积和全面积 能利用圆的弧长和扇形的面 积解决一些简单的实际问题 2 / 16 年份 题号 考法 分值 2015 填空 16 作图依据 3 分 解答 24 圆综合 5 分 解答 29 新定义 8 分 2016 填空 16 作图依据 3 分 解答 25 圆综合 5 分 解答 29 新定义 8 分 2017 填空 16 作图依据 3 分 解答 24 圆综合 5 分 解答 29 新定义 8 分 2018 填空 12 圆周角 2 分 解答 22 圆综合 5 分 解答 28 新定义 7 分 二、复习建议 1. 清除认知盲区 有关圆的计算：弧长、扇形、圆锥；圆中的分类讨论； 圆中相关定理的叙述；正多边形的 相关概念与计算；切线长定理. 2. 构建知识网络 圆作为初中几何唯一的曲线形图形，核心还是应用型知识。通过圆周角定理及其推论、垂 径定理将弧的性质转化为线段长度与角度大小是需要重点练习的技能。 3. 强化核心应用 圆周角定理及其推论、垂径定理（知二求四）、切线的性质与判定 4. 归纳解题思路或方法 圆综合（求线段长的基本思路、逆推分析）；新定义（交轨法）；几何综合（辅助圆） 5. 培养答题习惯 提升审题技能；发展运算素养；规范作答 三、课时安排 建议安排 4-5 课时 四、具体内容 （一）圆周角定理及其推论 1.（2014 北京）如图，⊙ O 的直径 AB 垂直于弦 CD ，垂足是 E ， 22.5A   ， 4OC  ， CD 的长为（ ）． A． 2 2 B． 4 C． 4 2 D． 8 3 / 16 2.（16.1 西城 8）如图，A，B，C 三点在已知的圆上，在△ABC 中， ∠ABC=70°，∠ACB=30°，D 是 的中点，连接 DB，DC，则∠DBC 的度数为 A．30° B．45° C．50° D．70° 3．已知，如图，AB 为⊙O 的直径，AB＝AC，BC 交⊙O 于点 D，AC 交⊙O 于 点 E，∠BAC＝450。给出以下五个结论：①∠EBC＝22.50；②BD＝DC ③AE＝2EC；④劣弧  AE 是劣弧  DE 的 2 倍；⑤AE＝BC；其中正确结论的序号 是______. 4.（2017•东城二模 14）如图，⊙O 的半径为 4，△ABC 是⊙O 的内接三角形，连接 OB，OC．若∠BAC 与∠BOC 互补，则弦 BC 的长为 ． 5.如图，AB 为⊙O 的直径，点 C 在⊙O 上，且∠CAB=30°， 点 D 为弧 AB 的中点，AC= 4 3 .则 CD 的长为 . 6.已知：如图，在△ABC 中，D 是 AB 边上一点，圆 O 过 D、B、 C 三点，∠DOC=2∠ACD=90°．如果∠ACB=75°，圆 O 的半径 为 2，则 BD 的长为 ． 7.已知：如图，A、B、C 为⊙O 上的三个点，⊙O 的直 径为 4cm，∠ACB=45°，则 AB 的长为 ． 8. （18 西城一模 13）如图，AB 为⊙O 的直径， C 为 AB 上一点，∠BOC=50°，AD∥OC，AD 交⊙O 于点 D，连接 AC，CD，那么∠ACD=__________． 9.（18 朝阳毕业 8）如图，四边形 ABCD 内接于⊙O，E 为 4 / 16 CD 延长线上一点，若∠ADE=110°，则∠AOC 的度数是（ ） A.70° B.110° C.140° D.160° 10.（18 朝阳一模 13）如图，点 A，B，C 在⊙O 上，四边形 OABC 是平行四边 形，OD⊥AB 于点 E，交⊙O 于点 D，则∠BAD= 度. 11.（18 海淀一模 14）如图，四边形 ABCD 是平行四边形，⊙O 经过点 A， C，D，与 BC 交于点 E，连接 AE，若∠D = 72°，则∠BAE = °. （二）垂径定理及其推论 1．如图，在⊙O 中，弦 AB 垂直平分半径 OC ．若⊙O 的半径为 4， 则弦 AB 的长为 （A） 32 （B） 34 （C） 52 （D） 54 2.（2017•朝阳）如图，⊙O 的半径 OC 垂直于弦 AB，垂足为 D， OA= 2 2 ，∠B=22.5°，AB 的长为 A．2 B．4 C． 2 2 D． 4 2 3. 一圆柱形排水管的截面如图所示，已知排水管的半径为 1m，水面 宽 AB 为 1.2m．由于天气下雨，水管水面上升，此时排水管水面宽变 为 1.6m，求水面上升的高度． 4．如图，⊙O 的半径 OD⊥弦 AB 于点 C，连结 AO 并延长交⊙O 5 / 16 于点E，连结 EC．若 AB=8，CD=2，求 EC 的长． 5.（18 石景山一模 13）如图， AB 是⊙ O 的直径， CD 是弦， CD AB 于点 E ，若⊙ O 的半径是 5 ， 8CD  ，则 AE  ． （三）弧长、扇形、圆锥与正多边形的计算 1．如图，⊙O 为正五边形 ABCDE 的外接圆，⊙O 的半 径为 2， 则 AB 的长为（ ） A. 5  B. 2 5  C. 3 5  D. 4 5  2.（2017•东城二模） 如图，一扇形纸扇完全打开后，外侧 两竹条 AB 和 AC 的夹角为 120°，竹条 AB 的长为 25cm，贴纸 部分的宽 BD 为 15cm，若纸扇两面贴纸，则一面贴纸的面积 为 cm2. （结果保留π） 3.如图，这是某同学用纸板做成的一个底面直径为 10cm，高为 12cm 的无底圆锥形玩具(接缝忽略不计) ，则做这个玩具所需纸板的面积是 _____________cm2(结果保留  )． 4.（2017 西城二模）如图，以点 O 为圆心，AB 为直径的半圆经 过点 C，若 C 为弧 AB 的中点，若 AB=2，则图中阴影部分的面积 是（ ） (A) 2  (B) 1 2 2  (C) 4  (D) 1 2 4  5.（18 朝阳毕业 10）如图，正方形 ABCD 的边长为 2，以 BC 为直径的半圆 与对角线 AC 相交于点 E，则图中阴影部分的面积为（ ） A.  4 1 2 3  B.  4 1 2 5  C.  2 1 2 5  D.  4 1 2 5  6 / 16 6.（18 东城一模 4）如图，圆 O 是等边 △ ABC 的外接圆，其半径为 3. 图中阴影部分的面积是（ ） A．π B． 3 π 2 C．2π D．3π （四）圆与坐标系 1.如图，在平面直角坐标系中，已知⊙O 的半径为 1，动直线 AB 与 x 轴交于点 P（x，0），直线 AB 与 x 轴正方向夹角为 45°，若直 线 AB 与⊙O 有公共点，则 x 的取值范围是 2. 的半径为 ，点 M 的坐标为（m,3）。若在 上存在一点 N， 使得点 M,N 所得直线与 x 轴成 45 度，求 m 的取值范围。 3.如图，在直角坐标系中，⊙A 的圆心 A 的坐标为（-1，0）， 半径为 1，点 P 为直线 34 3  xy 上的动点，过点 P 作⊙A 的切线，切点为 Q，则切线长 PQ 的最小值是__________ （五）尺规作图与作图依据 1.（18.1 海淀）下面是“作一个 30°角”的尺规作图过程． 已知：平面内一点 A． 求作：∠A，使得∠A 30°． 作法：如图， （1）作射线 AB； （2）在射线 AB 上取一点 O，以 O 为圆心，OA 为半径作圆， 与射线 AB 相交于点 C； （3）以 C 为圆心，OC 为半径作弧，与⊙O 交于点 D，作射 线 AD． ∠DAB 即为所求的角． 请回答：该尺规作图的依据是 ． 2.（17 北京）16.下图是“作已知直角三角形的外接圆”的尺规作图过程 已知： 0, 90Rt ABC C   ，求作 Rt ABC 的外接圆. 作法：如图． 7 / 16 （1）分别以点 A 和点 B 为圆心，大于 1 2 AB 的长为半径作弧，两弧相交于 ,P Q 两点； （2）作直线 PQ ，交 AB 于点 O ； （3）以 O 为圆心， OA 为半径作 O . ⊙O 即为所求作的圆. 请回答：该尺规作图的依据是 ． 3．尺规作图：如图，AC 为⊙O 的直径． （1）求作：⊙O 的内接正方形 ABCD．（要求：不写作法，保留作图 痕迹）； （2）当直径 AC=4 时，求这个正方形的边长． 4.（17.1 西城）考古学家发现了一块古代圆形残片如图所示，为了修复这块残片，需要找出圆 心. （1）请利用尺规作图确定这块残片的圆心 O； （2）写出作图的依据： ． （六）圆综合 1.（2015•北京）如图，AB 是⊙O 的直径，过点 B 作⊙O 的 切线 BM，弦 / /CD BM ，交 AB 于点 F，且 DA DC ， 链接 AC，AD，延长 AD 交 BM 地点 E。 (1)求证： ACD 是等边三角形。 (2)链接 OE，若 2DE  ，求 OE 的长。 2.（17.海淀）如图，在△ABC 中，点 O 在边 AC 上， ⊙O 与△ABC 的边 BC，AB 分别相切于 C，D 两点，与边 AC 交 于 E 点，弦 CF 与 AB 平行，与 DO 的延长线交于 M 点． （1）求证：点 M 是 CF 的中点； （2）若 E 是 DF 的中点，BC=a，写出求 AE 长的思路． 3.（17 丰台）如图，AB 是⊙O 的直径，C，D 为⊙O 上两点，CF⊥AB 于点 F，CE⊥AD 交 AD 的延长线于点 E， A B C D E F M O 8 / 16 且 CE=CF． （1）求证：CE 是⊙O 的切线； （2）连接 CD，CB．若 AD=CD=a，写出求四边 形 ABCD 面积的思路． 4.（17.西城）如图，AB 是⊙O 的直径，C 是⊙O 上一点，过点 B 作 ⊙O 的切线，与 AC 延长线交于点 D，连接 BC，OE∥BC 交⊙O 于点 E，连接 BE 交 AC 于点 H． （1）求证：BE 平分∠ABC； （2）连接 OD，若 BH=BD=2，求 OD 的长． 5.（17 石景山）如图，AC 是⊙O 的直径，点 D 是⊙O 上一点，⊙O 的切线 CB 与 AD 的延长线 交于点 B，点 F 是直径 AC 上一点， 连接 DF 并延长交⊙O 于点 E，连接 AE． （1）求证：∠ABC=∠AED； （2）连接 BF，若 AD 5 32 ，AF=6，tan 3 4AED ， 求 BF 的长． 6.（2017 北京）如图， AB 是⊙O 的一条弦， E 是 AB 的中点，过点 E 作 EC OA 于点C ，过点 B 作⊙O 的切线交 CE 的延长线于点 D . （1）求证： DB DE ； （2）若 12, 5AB BD  ，求⊙O 的半径. 7. 如图，AB 为⊙O 的直径，CB，CD 分别 9 / 16 切⊙O 于点 B，D，CD 交 BA 的延长线于点 E，CO 的延长 线交⊙O 于点 G，EF⊥OG 于点 F． （1）求证：∠FEB=∠ECF； （2）若 BC=6，DE=4，求 EF 的长． 8.（2012•北京）已知：如图， AB 是 O⊙ 的直径， C 是 O⊙ 上一点， OD BC⊥ 于点 D ，过点C 作 O⊙ 的切线，交 OD 的延长线于点 E ，连结 BE ． （1）求证： BE 与 O⊙ 相切； （2）连结 AD 并延长交 BE 于点 F ，若 9OB  ， 2sin 3ABC  ， 求 BF 的长． 9.（2011 北京）如图，在△ABC， AB AC ，以 AB 为直径的⊙O 分 别 交 AC 、 BC 于 点 D 、 E ， 点 F 在 AC 的 延 长 线 上 ， 且 1 2CBF CAB   。 （1）求证：直线 BF 是⊙O 的切线； （2）若 5AB  ， 5sin 5CBF  ，求 BC 和 BF 的长。 10．如图， △ 香䁨 内接于 ，过点 B 作 的切 线 ， 为射线 BD 上一点，连 接 CF． ′〵 求证： 䁨香 ； 〵 若 的直径为 ， 香 ， tan ，求 CF 的长． 11.（17 西城一模）如图，AB 是⊙O 的直径，C 是⊙O 上一点，过点 C 作⊙O 的切线，交 BA 的延长线交于点 D， 过点 B 作 BE⊥BA，交 DC 延长线于点 E，连接 OE，交⊙O 于点 F， 10 / 16 交 BC 于点 H，连接 AC． （1）求证：∠ECB= ∠EBC； （2）连接 BF，CF，若 CF=6，sin∠FCB= 3 5 ，求 AC 的长． 13.（2017•怀柔二模）如图，AB 是⊙O 的直径，CD 为⊙O 的弦，过点 B 作⊙O 的切线，交 AD 的延长线于点 E，连接 AC 并延长，过点 E 作 EG⊥AC 的延长线于点 G，并且 ∠GCD=∠GAB. （1）求证：  AC BD ； （2）若 AB=10，sin∠ADC= 5 3 ，求 AG 的长． 14.（17 丰台）如图， AB 是⊙O 的直径，点 C 是 »AB 的中点， 连接 AC 并延长至点 D ，使 CD AC ，点 E 是 OB 上一点， 且 2 3 OE EB  ， CE 的延长线交 DB 的延长线于点 F ， AF 交⊙O 于点 H ，连接 BH . （1）求证： BD 是⊙O 的切线； （2）当 2OB  时，求 BH 的长. 15.如图，A，B，C 三点在⊙O 上， 直径 BD 平分∠ABC，过点 D 作 DE∥AB 交弦 BC 于点 E，在 BC 的延长线上取一点 F，使得 EF DE． （1）求证：DF 是⊙O 的切线； （2）连接 AF 交 DE 于点 M，若 AD 4，DE 5， 求 DM 的长． 16.（2014•北京）如图，AB 是⊙O 的直径，C 是弧 AB 的中点， ⊙O 的切线 BD 交 AC 的延长线于点 D，E 是 OB 的中点， CE 的延长线交切线 BD 于点 F，AF 交⊙O 于点 H，连接 BH． （1）求证：AC=CD； 11 / 16 A F C O B M （2）若 OB=2，求 BH 的长． 17. 已知：AB 是⊙O 的弦，OD⊥AB 于 M 交⊙O 于点 D，CB⊥AB 交 AD 的延长线于 C． （1）求证：AD＝DC； （2）过 D 作⊙O 的切线交 BC 于 E，若 DE＝2，CE=1， 求⊙O 的半径． 18．如图，D 是⊙O 的直径 CA 延长线上一点，点 B 在⊙O 上，且 AB＝AD＝AO． （1）求证：BD 是⊙O 的切线； （2）若 E 是劣弧 BC 上一点，AE 与 BC 相交于点 F， △BEF 的面积为 8，且 cos∠BFA＝ 3 2 ， 求△ACF 的面积． 19. 如图，AB 为⊙O 的直径，AB=4，点 C 在⊙O 上， CF⊥OC，且 CF=BF. （1）证明 BF 是⊙O 的切线; （2）设 AC 与 BF 的延长线交于点 M，若 MC=6，求∠MCF 的大小. 20．已知：如图，⊙O 的半径 OC 垂直弦 AB 于点 H，连接 BC， 过点 A 作弦 AE∥BC，过点 C 作 CD∥BA 交 EA 延长线于点 D， 延长 CO 交 AE 于点 F． （1）求证：CD 为⊙O 的切线； （2）若 BC＝5，AB＝8，求 OF 的长． 21．如图所示，AB 是⊙O 的直径，OD⊥弦 BC 于点 F，且交⊙O 于点 E， 若∠AEC=∠ODB． （1）判断直线 BD 和⊙O 的位置关系，并给出证明； （2）当 AB=10，BC=8 时，求 BD 的长． E O B H C AD F 12 / 16 22．在Rt△AFD中，∠F=90°，点B、C分别在AD、FD上，以AB为直径的 半圆O 过点C，联结AC，将△AFC 沿AC翻折得△AEC ，且点E恰好 落在直径AB上. （1）判断：直线FC与半圆O的位置关系是_______________； 并证明你的结论. （2）若OB=BD=2,求CE的长． 23．已知 Rt△ABC 中，∠ABC=90°，以 AB 为直径作⊙O 交 AC 于点 D，连结 BD． （1）如图 1，若 BD∶CD＝3∶4，AD＝3，求⊙O 的直径 AB 的长； （2）如图 2，若 E 是 BC 的中点，连结 ED，请你判断直线 ED 与⊙O 的位置关系，并证明 你的结论． （七） 圆中的分类讨论 1.圆的一条弦把圆分成 1：4 两部分，则这条弦所对的圆周角大小为 . 2.点 A、B、C 为⊙O 上的两点， OBOC 70 ，求圆周角 BAC 的大小. 3.半径为 3 的圆 O 的一条弦 AB 的长为 3，点 C 在圆 O 上，则 ACB ＝ . 4.已知：点 P 到⊙O 最近的距离为 3，最远的距离为 11，求⊙O 的半径。 5.⊙O 半径为 10cm，弦 CDAB // ，若 AB＝12cm，CD＝16cm，求两弦的距离。 6.已知：⊙O 的半径 OA＝1，弦 AB、AC 的长分别为 3,2 ，求 BAC 的大小。 7.已知⊙O 的直径 AB 的长为 34，弦 CD 的长为 16， CDAB  ，求以 CD 为弦的弓形的高. 8.等腰三角形 ABC 内接于⊙O，AB＝AC ，若⊙O 的直径为 10，BC＝8，求该三角形底边上的 高。 13 / 16 9.在平面直角坐标系中，⊙O 的圆心在原点，半径为 2，点 A 的坐标为 )32,2( ，直线 AB 为 ⊙O 切线，B 为切点，求点 B 点的坐标。 10.已知 中ABC 4,390C o  BCAC，＝ ，若以 C 为圆心，R 为半径作⊙C 与斜边 AB 只 有一个公共点，求 R 的取值范围. （八）新定义 1.（18 海淀一模 15）定义：圆中有公共端点的两条弦组成的折线称为圆的一条折弦． 阿基米德折弦定理：如图 1，AB 和 BC 组成圆的 折 弦 ， AB BC ， M 是 弧 ABC 的 中 点 ， MF AB 于 F ，则 AF FB BC  ． 如图 2，△ ABC 中， 60ABC   ， 8AB  ， 6BC  ， D 是 AB 上 一 点 ， 1BD  ， 作 DE AB 交△ ABC 的外接圆于 E ，连接 EA， 则 EAC =________°． 2.（18 石景山一模 28）对于平面上两点 A，B，给出如下定义：以点 A 或 B 为圆心，AB 长为半径的圆称为点 A，B 的“确定圆”．如图为点 A，B 的“确定圆”的示意图．．．． （1）已知点 A 的坐标为 ( 1,0) ，点 B 的坐标为 (3,3) ，则点 A，B 的 “确定圆”的面积为_________； （2）已知点 A 的坐标为 (0,0) ，若直线 y x b  上只存在一个点 B，使得点 A，B 的“确 定圆”的面积为 9 ，求点 B 的坐标； （3）已知点 A 在以 ( 0)P m， 为圆心，以 1 为半径的圆上，点 B 在直线 3 33y x   上， 若要使所有点 A，B 的“确定圆”的面积都不小于 9 ，直接写出 m 的取值范围． 3.（18 西城一模 28）对于平面内的⊙ C 和⊙ C 外一点 Q ，给出如下定义：若过点 Q 的直线与 ⊙ C 存在公共点，记为点 A ， B ，设 AQ BQk CQ  ，则称点 A （或点 B ）是⊙ C 的“ k 相 关依附点”，特别地，当点 A 和点 B 重合时，规定 AQ BQ ， 2AQk CQ  （或 2BQ CQ ）． 已知在平面直角坐标系 xOy 中， ( 1,0)Q  ， (1,0)C ，⊙ C 的半径为 r ． （1）如图1 ，当 2r  时， ①若 1(0,1)A 是⊙ C 的“ k 相关依附点”，则 k 的值为__________． ② 2 (1 2,0)A  是否为⊙ C 的“ 2 相关依附点”．答：__________（填“是”或“否”）． （2）若⊙ C 上存在“ k 相关依附点”点 M ， 14 / 16 ①当 1r  ，直线 QM 与⊙ C 相切时，求 k 的值． ②当 3k  时，求 r 的取值范围． （3）若存在 r 的值使得直线 3y x b   与⊙ C 有公共点，且公共点是⊙ C 的“ 3 相关 依附点”，直接写出 b 的取值范围． 3.（18 怀柔一模 28）P 是⊙C 外一点，若射线．．PC 交⊙C 于点 A，B 两点，则给出如下定义：若 0＜PA  PB≤3，则点 P 为⊙C 的“特征点”． （1）当⊙O 的半径为 1 时． ①在点 P1（ 2 ,0）、P2（0,2）、P3（4，0）中，⊙O 的“特征点”是 ； ②点 P 在直线 y=x+b 上，若点 P 为⊙O 的“特征 点”．求 b 的取值范围； （2）⊙C 的圆心在 x 轴上，半径为 1，直线 y=x+1 与 x 轴，y 轴分别交于点 M，N，若线段 MN 上的所有点都不．． 是．⊙C 的“特征点”，直接写出点 C 的横坐标的取值范围． 4.（18 海淀一模 28）在平面直角坐标系 xOy 中，对于点 P 和⊙C ，给出如下定义：若⊙C 上 存在一点T 不与 O 重合，使点 P 关于直线 OT 的对称点 'P 在⊙ C 上，则称 P 为⊙ C 的反射 点．下图为⊙C 的反射点 P 的示意图． （1）已知点 A 的坐标为 (1,0) ，⊙ A的半径为 2 ， ①在点 (0,0)O ， (1,2)M ， (0, 3)N  中，⊙ A的反射点是____________； ②点 P 在直线 y x  上，若 P 为⊙ A的反射点，求点 P 的横坐标的取值范围； 15 / 16 （2）⊙C 的圆心在 x 轴上，半径为 2 ，y 轴上存在点 P 是⊙C 的反射点，直接写出圆心C 的横坐标 x 的取值范围． 5.（2013 北京中考）对于平面直角坐标系 O 中的点 P 和⊙C，给出如下定义：若⊙C 上存在 两个点 A，B，使得∠APB=60°，则称 P 为⊙C 的关联点。 已知点 D（ ， ），E（0，-2），F（ ，0） （1）当⊙O 的半径为 1 时， ①在点 D，E，F 中，⊙O 的关联点是__________； ②过点 F 作直线交 轴正半轴于点 G，使∠GFO=30°，若直线上的点 P（ ， ）是⊙O 的关 联点，求 的取值范围； （2）若线段 EF 上的所有点都是某个圆的关联点，求这个圆的半径 的取值范围。 6.（2015 中考）在平面直角坐标系 xOy 中， C 的半径为 r，P 是与圆心 C 不重合的点，点 P 关于 O 的反称点的定义如下：若在射线．．CP 上存在一点 P，满足 2CP CP r  ，则称 P为 点 P 关于⊙C 的反称点，下图为点 P 及其关于⊙C 的反称点 P的示意图 (1)当⊙O 的半径为 1 时。 ①分别判断点 (2,1)M ， 3( ,0)2N ， (1, 3)T 关于⊙O 的反称点是否 存在，若存在？求其坐标； ②点 P 在直线 2y x   上，若点 P 关于⊙O 的反称点 P存在， 且点 P不在 x 轴上，求点 P 的横坐标的取值范围； (2)当⊙C 的圆心在 x 轴上，半径为 1，直线 3 2 33y x   与 x 轴， y 轴分别交于点 A，B，若线段 AB 上存在点 P，使得点 P 关于⊙C 的反称点 P在⊙C 的内部， 求圆心 C 的横坐标的取值范围。 y 1 O C x 1 P 16 / 16 7.（2017 中考）在平面直角坐标系 xOy 中的点 P 和图形 M ，给出如下的定义：若在图形 M 上 存在一点Q ，使得 P Q、 两点间的距离小于或等于 1，则称 P 为图形 M 的关联点． （1）当 O 的半径为 2 时， ①在点 1 2 3 1 1 3 5,0 , , , ,02 2 2 2P P P               中，⊙O 的关联点是_______________． ②点 P 在直线 y x  上，若 P 为⊙O 的关联点，求点 P 的横坐标的取值范围． （2）⊙C 的圆心在 x 轴上，半径为 2，直线 1y x   与 x 轴、 y 轴交于点 A B、 ．若线段 AB 上的所有点都是⊙C 的关联点，直接写出圆心C 的横坐标的取值范围．