2008年海南省高考数学试卷（文）【附答案、word版本，可再编辑；B4纸型两栏】

2008年海南省高考数学试卷（文）【附答案、word版本，可再编辑；B4纸型两栏】

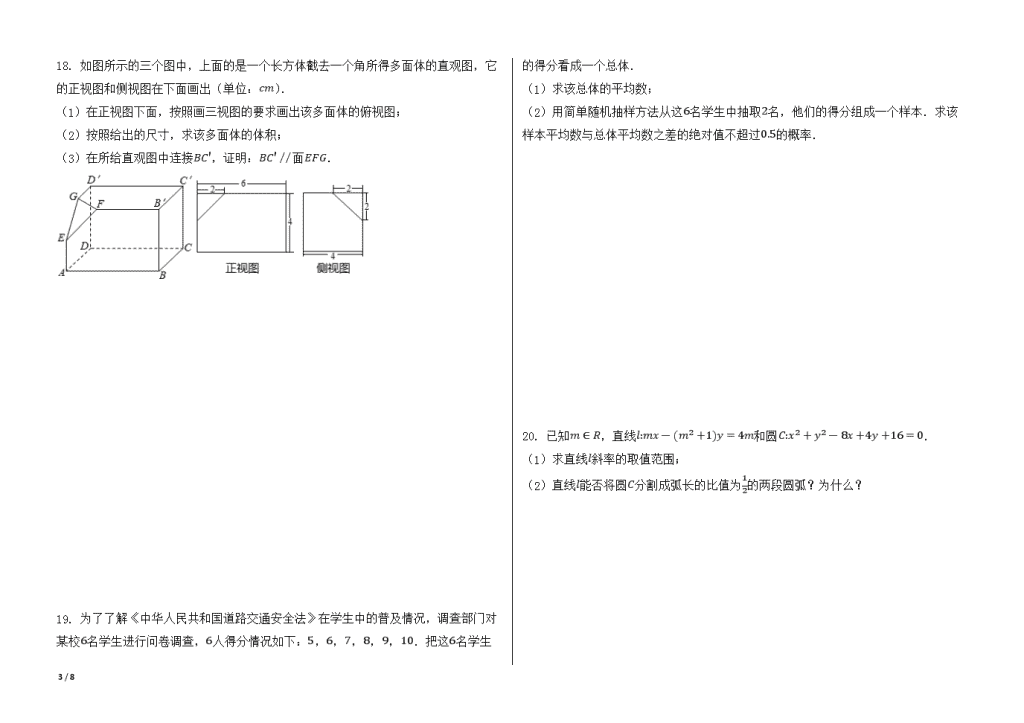
‎2008年海南省高考数学试卷（文）‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1. 已知集合M＝‎{x|(x+2)(x-1)<0}‎，N＝‎{x|x+1<0}‎，则M∩N＝（ ）‎ A.‎(-1, 1)‎ B.‎(-2, 1)‎ C.‎(-2, -1)‎ D.‎‎(1, 2)‎ ‎2. 双曲线x‎2‎‎10‎‎-y‎2‎‎2‎=1‎的焦距为‎(‎        ‎‎)‎ A.‎3‎‎2‎ B.‎4‎‎2‎ C.‎3‎‎3‎ D.‎‎4‎‎3‎ ‎3. 已知复数z=1-i，则z‎2‎z-1‎‎=(‎ ‎‎)‎ A.‎2‎ B.‎-2‎ C.‎2i D.‎‎-2i ‎4. 设f(x)=xlnx，若f'(x‎0‎)=2‎，则x‎0‎‎=(‎ ‎‎)‎ A.e‎2‎ B.e C.ln2‎‎2‎ D.‎ln2‎ ‎5. 已知平面向量a‎→‎‎=(1, -3)‎，b‎→‎‎=(4, -2)‎，λa‎→‎+‎b‎→‎与a‎→‎垂直，则λ是（ ）‎ A.‎-1‎ B.‎1‎ C.‎-2‎ D.‎‎2‎ ‎6. 下面程序框图，如果输入三个实数a、b、c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（ ）‎ A.c>x B.x>c C.c>b D.‎b>c ‎7. 已知a‎1‎‎>a‎2‎>a‎3‎>0‎，则使得‎(1-aix‎)‎‎2‎<1(i=1, 2, 3)‎都成立的x的取值范围是‎(‎        ‎‎)‎ A.‎(0,‎1‎a‎1‎)‎ B.‎(0,‎2‎a‎1‎)‎ C.‎(0,‎1‎a‎3‎)‎ D.‎‎(0,‎2‎a‎3‎)‎ ‎8. 设等比数列‎{an}‎的公比q=2‎，前n项和为Sn，则S‎4‎a‎2‎‎=(‎ ‎‎)‎ A.‎2‎ B.‎4‎ C.‎15‎‎2‎ D.‎‎17‎‎2‎ ‎9. 平面向量a‎→‎，b‎→‎共线的充要条件是（ ）‎ A.a‎→‎，b‎→‎方向相同 B.a‎→‎，b‎→‎两向量中至少有一个为零向量 C.‎∃λ∈R，‎b‎→‎‎=λa‎→‎ D.存在不全为零的实数λ‎1‎，λ‎2‎，‎λ‎1‎a‎→‎‎+λ‎2‎b‎→‎=‎‎0‎‎→‎ ‎10. 点P(x, y)‎在直线‎4x+3y=0‎上，且x，y满足‎-14≤x-y≤7‎，则点P到坐标原点距离的取值范围是（ ）‎ A.‎[0, 5]‎ B.‎[0, 10]‎ C.‎[5, 10]‎ D.‎‎[5, 15]‎ ‎11. 函数f(x)=cos2x+2sinx的最小值和最大值分别为(        )‎ A.‎-3‎，‎1‎ B.‎-2‎，‎2‎ C.‎-3‎，‎3‎‎2‎ D.‎-2‎，‎‎3‎‎2‎ ‎12. 已知平面α⊥‎平面β，α∩β＝l，点A∈α，A∉l，直线AB // l，直线AC⊥l，直线m // α，m // β，则下列四种位置关系中，不一定成立的是（ ）‎ ‎ 8 / 8‎ A.AB // m B.AC⊥m C.AB // β D.‎AC⊥β 二、填空题（共4小题，每小题5分，满分20分）‎ ‎13. 已知‎{an}‎为等差数列，a‎3‎‎+a‎8‎=22‎，a‎6‎‎=7‎，则a‎5‎‎=‎________．‎ ‎14. 一个六棱柱的底面是正六边形，其侧棱垂直底面．已知该六棱柱的顶点都在同一个球面上，且该六棱柱的高为‎3‎，底面周长为‎3‎，那么这个球的体积为________．‎ ‎15. 过椭圆x‎2‎‎5‎‎+y‎2‎‎4‎=1‎的右焦点作一条斜率为‎2‎的直线与椭圆交于A、B两点，O为坐标原点，则‎△OAB的面积为________．‎ ‎16. 从甲、乙两品种的棉花中各抽测了‎25‎根棉花的纤维长度（单位：mm），结果如下：‎ 甲品种：‎271 273 280 285 285‎  ‎‎287 292 294 295 301 303 303 307‎ ‎308 310 314 319 323 325 325‎‎  ‎‎328 331 334 337 352‎ 乙品种：‎‎284 292 295 304 306 307 312 313 315 315 316 318 318‎ ‎320 322 322 324 327 329 331 333 336 337 343 356‎ 由以上数据设计了如下茎叶图：‎ 根据以上茎叶图，对甲、乙两品种棉花的纤维长度作比较，写出两个统计结论：‎ ‎①________；‎ ‎②________．‎ 三、解答题（共7小题，22题，23题选做一题。满分70分）‎ ‎17. 如图，‎△ACD是等边三角形，‎△ABC是等腰直角三角形，‎∠ACB=‎‎90‎‎∘‎，BD交AC于E，AB=2‎．‎ ‎（1）求cos∠CBE的值；‎ ‎（2）求AE．‎ ‎ 8 / 8‎ ‎18. 如图所示的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出（单位：cm）．‎ ‎（1）在正视图下面，按照画三视图的要求画出该多面体的俯视图；‎ ‎（2）按照给出的尺寸，求该多面体的体积；‎ ‎（3）在所给直观图中连接BC'‎，证明：BC' // ‎面EFG．‎ ‎19. 为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门对某校‎6‎名学生进行问卷调查，‎6‎人得分情况如下：‎5‎，‎6‎，‎7‎，‎8‎，‎9‎，‎10‎．把这‎6‎名学生的得分看成一个总体．‎ ‎（1）求该总体的平均数；‎ ‎（2）用简单随机抽样方法从这‎6‎名学生中抽取‎2‎名，他们的得分组成一个样本．求该样本平均数与总体平均数之差的绝对值不超过‎0.5‎的概率．‎ ‎20. 已知m∈R，直线l:mx-(m‎2‎+1)y=4m和圆C:x‎2‎+y‎2‎-8x+4y+16=0‎．‎ ‎（1）求直线l斜率的取值范围；‎ ‎（2）直线l能否将圆C分割成弧长的比值为‎1‎‎2‎的两段圆弧？为什么？‎ ‎ 8 / 8‎ ‎21. 设函数f(x)=ax-‎bx，曲线y=f(x)‎在点（‎2, f(2)‎）处的切线方程为‎7x-4y-12=0‎．‎ ‎（1）求y=f(x)‎的解析式；‎ ‎（2）求证：曲线y=f(x)‎上任一点处的切线与直线x=0‎和直线y=x所围成的三角形面积为定值，并求此定值．‎ ‎22. 如图，过圆O外一点M作它的一条切线，切点为A，过A作直线AP垂直直线OM，垂足为P．‎ ‎（1）证明：OM⋅OP＝OA‎2‎；‎ ‎（2）N为线段AP上一点，直线NB垂直直线ON，且交圆O于B点．过B点的切线交直线ON于K．证明：‎∠OKM＝‎90‎‎∘‎．‎ ‎ 8 / 8‎ ‎23. 自选题：已知曲线C‎1‎‎:‎x=cosθy=sinθ（θ为参数），曲线C‎2‎‎:‎x=‎2‎‎2‎t-‎‎2‎y=‎2‎‎2‎t（t为参数）．‎ ‎（1）指出C‎1‎，C‎2‎各是什么曲线，并说明C‎1‎与C‎2‎公共点的个数；‎ ‎（2）若把C‎1‎，C‎2‎上各点的纵坐标都压缩为原来的一半，分别得到曲线C‎1‎‎'‎，C‎2‎‎'‎．写出C‎1‎‎'‎，C‎2‎‎'‎的参数方程．C‎1‎‎'‎与C‎2‎‎'‎公共点的个数和C与C‎2‎公共点的个数是否相同？说明你的理由．‎ ‎ 8 / 8‎ 参考答案与试题解析 ‎2008年海南省高考数学试卷（文）‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1.C ‎2.D ‎3.A ‎4.B ‎5.A ‎6.A ‎7.B ‎8.C ‎9.D ‎10.B ‎11.C ‎12.D 二、填空题（共4小题，每小题5分，满分20分）‎ ‎13.‎‎15‎ ‎14.‎‎4π‎3‎ ‎15.‎‎5‎‎3‎ ‎16.乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度,乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度 三、解答题（共7小题，22题，23题选做一题。满分70分）‎ ‎17.解：．（1）∵ ‎∠BCD=‎90‎‎∘‎+‎60‎‎∘‎=‎‎150‎‎∘‎，‎CB=AC=CD ‎∴ ‎∠CBE=‎‎15‎‎∘‎，∴ cos∠CBE=cos(‎45‎‎∘‎-‎30‎‎∘‎)=‎‎6‎‎+‎‎2‎‎4‎．‎ ‎（2）在‎△ABE中，AB=2‎，由正弦定理得AEsin(‎45‎‎∘‎-‎15‎‎∘‎)‎‎=‎‎2‎sin(‎90‎‎∘‎+‎15‎‎∘‎)‎，‎ 故AE=‎2sin‎30‎‎∘‎cos‎15‎‎∘‎=‎2×‎‎1‎‎2‎‎6‎‎+‎‎2‎‎4‎=‎6‎-‎‎2‎．‎ ‎18.解：（1）如图 ‎（2）所求多面体的体积V=V长方体-V正三棱锥=4×4×6-‎1‎‎3‎×(‎1‎‎2‎×2×2)×2=‎284‎‎3‎(cm‎3‎)‎ ‎（3）证明：如图，‎ 在长方体ABCD-A'B'C'D'‎中，连接AD'‎，则AD' // BC'‎ 因为E，G分别为AA'‎，A'D'‎中点，所以AD' // EG，从而EG // BC'‎，‎ 又EG⊂‎平面EFG，所以BC' // ‎平面EFG；‎ ‎19.解：（1）总体平均数为‎1‎‎6‎‎(5+6+7+8+9+10)=7.5‎ ‎（2）设A表示事件“样本平均数与总体平均数之差的绝对值不超过‎0.5‎”‎ 从总体中抽取‎2‎个个体全部可能的基本结果有：‎(5, 6)‎，‎(5, 7)‎，‎(5, 8)‎，‎(5, 9)‎，‎ ‎ 8 / 8‎ ‎(5, 10)‎‎，‎(6, 7)‎，‎(6, 8)‎，‎(6, 9)‎，‎(6, 10)‎，‎(7, 8)‎，‎(7, 9)‎，‎(7, 10)‎，‎ ‎(8, 9)‎‎，‎(8, 10)‎，‎(9, 10)‎，共‎15‎个基本结果．‎ 事件A包含的基本结果有：‎(5, 9)‎，‎(5, 10)‎，‎(6, 8)‎，‎(6, 9)‎，‎(6, 10)‎，‎ ‎(7, 8)‎‎，‎(7, 9)‎，共有‎7‎个基本结果；‎ ‎∴ 所求的概率为P(A)=‎‎7‎‎15‎ ‎20.解：（1）直线l的方程可化为y=mm‎2‎‎+1‎x-‎‎4mm‎2‎‎+1‎，此时斜率k=‎mm‎2‎‎+1‎，‎ 即km‎2‎-m+k=0‎，∵ ‎△≥0‎，∴ ‎1-4k‎2‎≥0‎，‎ 所以，斜率k的取值范围是‎[-‎1‎‎2‎，‎1‎‎2‎]‎．‎ ‎（2）不能．由‎(1‎知l的方程为y=k(x-4)‎，其中‎|k|≤‎‎1‎‎2‎；‎ 圆C的圆心为C(4, -2)‎，半径r=2‎；圆心C到直线l的距离d=‎‎2‎‎1+‎k‎2‎ 由‎|k|≤‎‎1‎‎2‎，得d≥‎4‎‎5‎>1‎，即d>‎r‎2‎，‎ 从而，若l与圆C相交，则圆C截直线l所得的弦所对的圆心角小于‎2π‎3‎，‎ 所以l不能将圆C分割成弧长的比值为‎1‎‎2‎的两段弧．‎ ‎21. 解：（1）方程‎7x-4y-12=0‎可化为y=‎7‎‎4‎x-3‎，‎ 则f‎'‎‎(2)=‎‎7‎‎4‎.‎ 当x=2‎时，y=‎‎1‎‎2‎，即f(2)=‎‎1‎‎2‎ 又f‎'‎‎(x)=a+‎bx‎2‎，于是‎2a-b‎2‎=‎‎1‎‎2‎a+b‎4‎=‎‎7‎‎4‎，‎ 解得a=1‎b=3‎，故f(x)=x-‎‎3‎x．‎ ‎（2）设P(x‎0‎, y‎0‎)‎为曲线上任意一点，由f‎'‎‎(x)=1+‎‎3‎x‎2‎知曲线 在点P(x‎0‎, y‎0‎)‎处的切线方程为y-y‎0‎=(1+‎3‎x‎0‎‎2‎)(x-x‎0‎)‎，‎ 即y-(x‎0‎-‎3‎x‎0‎)=(1+‎3‎x‎0‎‎2‎)(x-x‎0‎)‎.‎ 令x=0‎，得y=-‎‎6‎x‎0‎，‎ 则切线与直线x=0‎的交点坐标为‎(0,-‎6‎x‎0‎)‎；‎ 令y=x，得y=x=2‎x‎0‎，则切线与直线y=x的交点坐标为‎(2x‎0‎, 2x‎0‎)‎.‎ 所以曲线在点P(x‎0‎, y‎0‎)‎处的切线与直线x=0‎，y=x所围成的三角形面积 为‎1‎‎2‎‎⋅|-‎6‎x‎0‎|⋅|2x‎0‎|=6‎．‎ 故曲线y=f(x)‎上任意一点处的切线与直线x=0‎和 y=x所围成的三角形面积为定值，此定值为‎6‎．‎ ‎22.因为MA是圆O的切线，‎ 所以OA⊥AM，又因为AP⊥OM，‎ 在Rt△OAM中，由射影定理知OA‎2‎＝OM⋅OP，‎ 故OM⋅OP＝OA‎2‎得证．‎ 因为BK是圆O的切线，BN⊥OK，同（1）有：‎ OB‎2‎‎＝ON⋅OK，又OB＝OA，‎ 所以OM⋅OP＝ON⋅OK，即ONOP‎=‎OMOK，又‎∠NOP＝‎∠MOK，‎ 所以‎△ONP∼△OMK，‎ 故‎∠OKM＝‎∠OPN＝‎90‎‎∘‎．‎ 即有：‎∠OKM＝‎90‎‎∘‎．‎ ‎23.解：（1）C‎1‎是圆，C‎2‎是直线．C‎1‎的普通方程为x‎2‎‎+y‎2‎=1‎，‎ 圆心C‎1‎‎(0, 0)‎，半径r=1‎．C‎2‎的普通方程为x-y+‎2‎=0‎．‎ 因为圆心C‎1‎到直线x-y+‎2‎=0‎的距离为‎1‎，‎ 所以C‎2‎与C‎1‎只有一个公共点．‎ ‎（2）压缩后的参数方程分别为C‎1‎‎':‎x=cosθy=‎1‎‎2‎sinθ（θ为参数）；‎ ‎ 8 / 8‎ C‎2‎‎':‎x=‎2‎‎2‎t-‎‎2‎y=‎2‎‎4‎t‎（t为参数）．‎ 化为普通方程为：C‎1‎‎':x‎2‎+4y‎2‎=1‎，C‎2‎‎':y=‎1‎‎2‎x+‎‎2‎‎2‎，‎ 联立消元得‎2x‎2‎+2‎2‎x+1=0‎，‎ 其判别式‎△=(2‎2‎‎)‎‎2‎-4×2×1=0‎，‎ 所以压缩后的直线C‎2‎‎'‎与椭圆C‎1‎‎'‎仍然只有一个公共点，和C‎1‎与C‎2‎公共点个数相同．‎ ‎ 8 / 8‎