- 2021-02-27 发布 |
- 37.5 KB |
- 3页

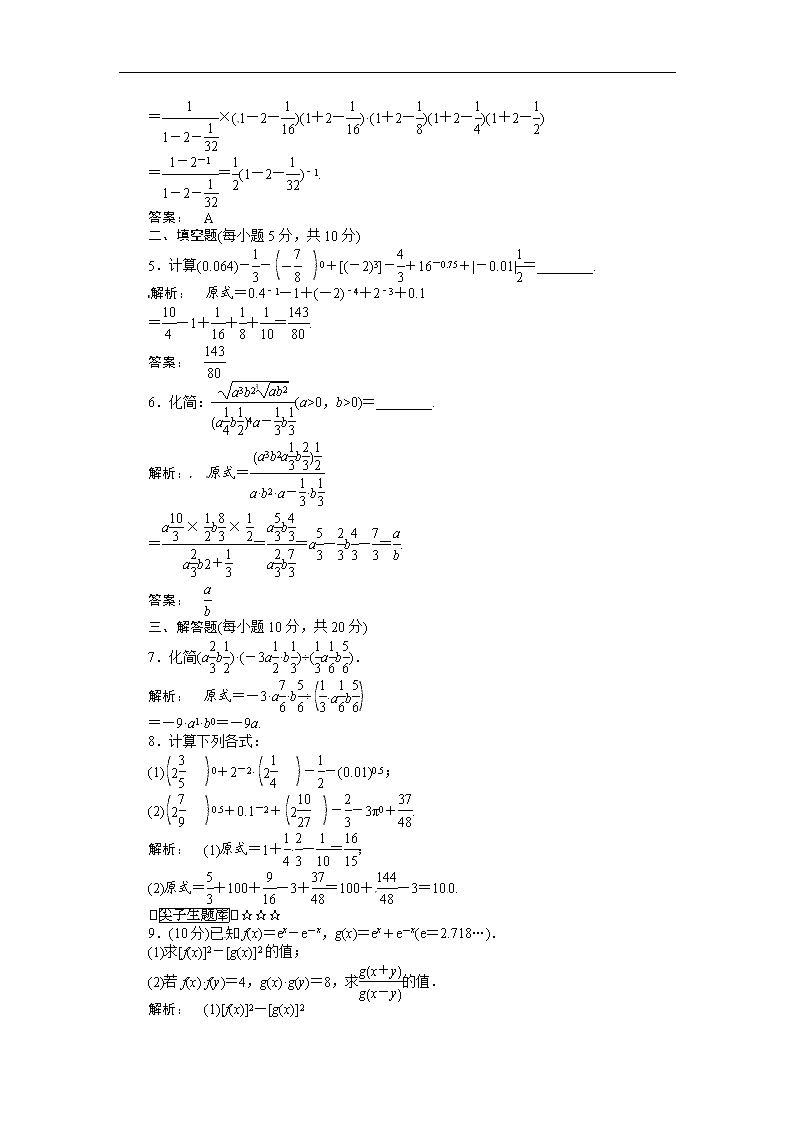

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学人教A版必修一教学训练(教师版)2_1_1_2
(本栏目内容,在学生用书中以活页形式分册装订!) 一、选择题(每小题5分,共20分) 1.化简[]的结果为( )[来源:Z§xx§k.Com] A.5 B. C.- D.-5 解析: []=() =5×=5=. 答案: B 2.下列结论中,正确的个数是( ) ①若a∈R,则(a2-2a+1)0=1; ②若a>b>0,则=1成立;[来源:Z_xx_k.Com] ③-n=n(ab>0); ④==(a≠b,ab≠0). A.1 B.2 C.3 D.4 解析: ①中,当a=1时,a2-2a+1=0,(a2-2a+1)0无意义,故错; ②③正确运用了幂的运算性质,正确; ④先变形又利用了幂的运算性质,正确.故选C. 答案: C 3.设a-a-=m,则=( ) A.m2-2 B.2-m2 C.m2+2 D.m2 解析: 将a-a-=m平方得(a-a-)2=m2, 即a-2+a-1=m2,所以a+a-1=m2+2, 即a+=m2+2⇒=m2+2.[来源:学,科,网Z,X,X,K] 答案: C 4.化简:(1+2-)(1+2-)(1+2-)(1+2-)(1+2-)的结果是( ) A.(1-2-)-1 B.(1-2)-1 C.1-2- D.(1-2-) 解析: (1+2-)(1+2-)(1+2-)(1+2-)(1+2-) =×(1-2-)(1+2-)(1+2-)(1+2-)(1+2-)(1+2-) =×(1-2-)(1+2-)·(1+2-)(1+2-)(1+2-) ==(1-2-)-1. 答案: A 二、填空题(每小题5分,共10分) 5.计算(0.064)--0+[(-2)3]-+16-0.75+|-0.01|=________. 解析: 原式=0.4-1-1+(-2)-4+2-3+0.1 =-1+++=. 答案: 6.化简:(a>0,b>0)=________. 解析: 原式= ===a-b-=. 答案: 三、解答题(每小题10分,共20分) 7.化简(ab)·(-3a·b)÷(ab). 解析: 原式=-3·a·b÷ =-9·a1·b0=-9a. 8.计算下列各式: (1)0+2-2·--(0.01)0.5; (2)0.5+0.1-2+--3π0+. 解析: (1)原式=1+·-=; (2)原式=+100+-3+=100+-3=100. ☆☆☆ 9.(10分)已知f(x)=ex-e-x,g(x)=ex+e-x(e=2.718…). (1)求[f(x)]2-[g(x)]2的值; (2)若f(x)·f(y)=4,g(x)·g(y)=8,求的值. 解析: (1)[f(x)]2-[g(x)]2 =[f(x)+g(x)][f(x)-g(x)][来源:学#科#网] =[(ex-e-x)+(ex+e-x)][(ex-e-x)-(ex-e-x)] =2ex·(-2e-x)=-4. (2)∵f(x)·f(y)=(ex-e-x)(ey-e-y) =ex+y-ex-y-ey-x+e-(x+y), g(x)·g(y)=(ex+e-x)(ey+e-y) =ex+y+ex-y+ey-x+e-(x+y), g(x+y)=ex+y+e-(x+y),g(x-y)=ex-y+e-(x-y)=ex-y+ey-x, ∴[来源:Z+xx+k.Com] 解得 ∴==3.查看更多