- 2021-02-27 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级数学下册教案-6 数学思考-人教版 (11)
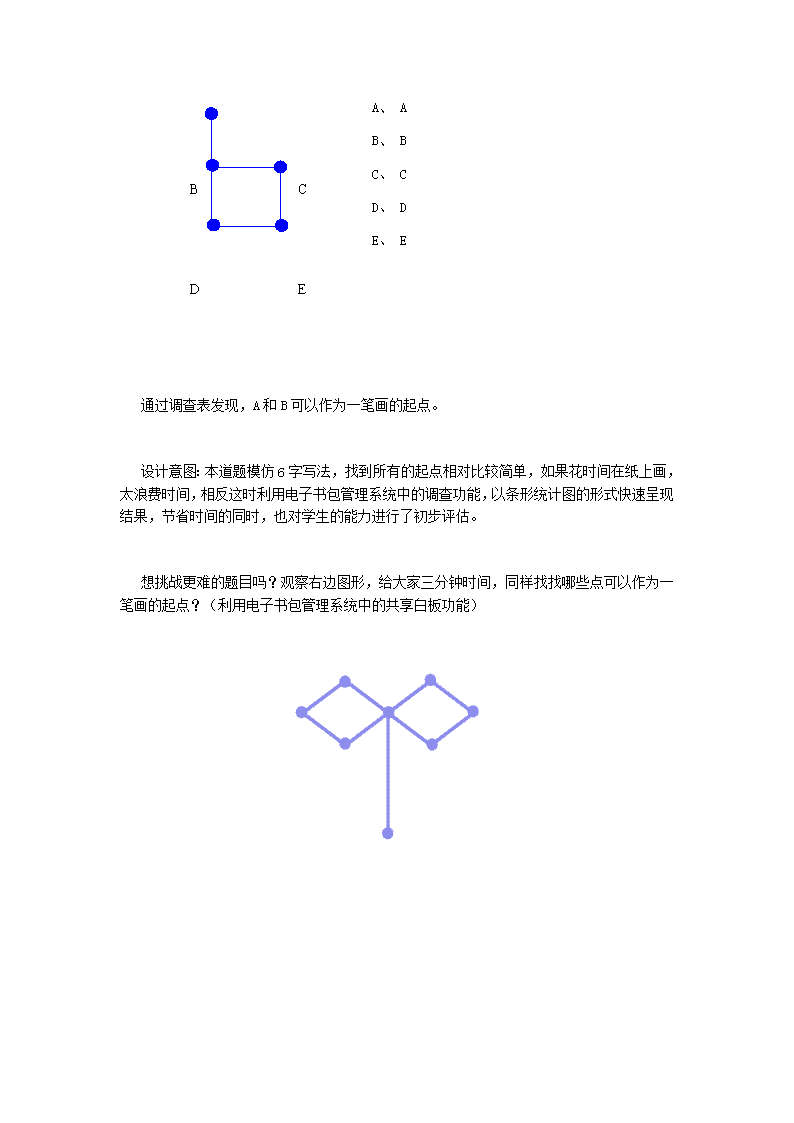
数学思考 教学内容: 新人教版六年级下册数学书 P104. 学情分析:四年级学生处在思维成长的活跃期,动手和推理能力初步形成,但欧拉一笔画原 理本身对于他们比较难理解,希望借助多媒体技术,完成这节跨学段课的学习,完成对一笔 画原理的初步认识和应用。 教学目标: 1、 了解什么是奇点,什么是偶点。 2、 掌握快速找到一笔画起点的方法。 3、 在分层练习的过程中,选择不同难度关卡的过程中,培养自信心,锻炼学习能力、克服 困难的意志。 4、 最后的思考环节,培养勇于探索的精神,同时扩大知识视野,激发学习兴趣。 5、 在从现实问题抽象成图形一笔画问题的过程,培养建模意识。 教学重点: 1、 了解奇点和偶点。 2、 掌握快速找到一笔画起点的方法。 教学难点: 在有两个奇点的图中,发现只有奇点可做起点。 教学准备: 电子书包管理系统、平板电脑、西沃 5、交互式白板。 教学过程: 1、 情景导入 呆头带大家到了迪斯尼。提出问题:沿途风景和有趣的项目,一次玩遍怎么走?(动画 将现实图抽象成由点和线组成的图形) 讨论得出:不重复、不遗漏。 设计意图:利用学生超级喜欢的漫画人物呆头作为引子,配合上西沃 5 的蒙层功能将人 物事先隐藏起来,留有神秘感。当教师说:“带大家见个老朋友”时,学生纷纷揣测,最后 发现擦出的是呆头,瞬间点燃学习热情。趁热打铁,构建了一笔画的模型。 2、课题引入 要想不重复、不遗漏地玩遍,需要用到一笔画的知识,现通过游戏来认识它。 阅读游戏指南:1、标出起点 s; 2、不重复和不遗漏地一笔画完。 想想在操作过程中,要注意什么? 起点 s、不重复、不遗漏、一笔画完。 让 2 位学生上台尝试,发现不是所有的点都能作为一笔画的起点。 引出课题:如何在这么多个点中快速找到起点,这就是今天所有学习的主要内容一笔画 之找起点。 设计意图:利用西沃白板制作一笔画游戏界面,建立游戏背景,激发学生兴趣。利用交 互动白板进行现场操作,有效地吸引学生的注意力,及时生成有用资源,引发学生思考,从 而提出问题,产生学习自主性。 3、 学习新知 (1)2 个奇点的情况。 观察左边图形,完成调查表。(利用电子书包管理系统中的调查功能) 在左图中,哪些能够作为一笔画的起点? A、 A B、 B C、 C D、 D E、 E 通过调查表发现,A 和 B 可以作为一笔画的起点。 设计意图:本道题模仿 6 字写法,找到所有的起点相对比较简单,如果花时间在纸上画, 太浪费时间,相反这时利用电子书包管理系统中的调查功能,以条形统计图的形式快速呈现 结果,节省时间的同时,也对学生的能力进行了初步评估。 想挑战更难的题目吗?观察右边图形,给大家三分钟时间,同样找找哪些点可以作为一 笔画的起点?(利用电子书包管理系统中的共享白板功能) B A C ED 大屏观看学生完成情况,针对性加以指导。 发现哪些点可以作为一笔画的起点?(大部分学生会选择 A 和 H,如果还有其它答案, 可以请他上台操作,及时纠错) 观察这些起点,小组讨论,____点可以作为起点。(直接用西沃 5 中的图层设计,将所 有起点浮至顶层。) 通过讨论发现,线条数是单数。(同时上台验证,边数边标) 这样从一点出发线条数为单数的点称为奇点。 观察这两幅图形,除了这些点还有奇点吗?谁来验证?那这些点应该叫做 ______。(偶点)看来只有奇点可作起点,偶点不行。左边这幅有两个奇点,右 边这幅也有两个奇点。 总结:有两个奇点时,只有奇点可作起点。看来要想找到起点,其实就是去 找____(奇点)。 设计意图:本环节先利用电子书包的共享白板功能,将图 2 共享给学生,学 生在 pad 上直接操作寻找答案,同时教师在互动白板上可以看到每个同学的作 品,从而可以进行针对性的指导。接着利用互动白板的截图功能,及时捕捉深层 素材,同时配合聚光灯,将学生的注意力停留在点和线上,从而突破难点。如果 遇到问题也可以上台直接操作和校正。 (2)进行巩固。 老师发送了 4 种不同难度的关卡,选择其中一关,利用今天所学的方法。快 速找到所有的起点。(利用电子书包监控功能,进行展示) B A C E D F G H 1 3 5 1 让学生自己讲解,如何快速找到所有的起点。 设计意图:这里利用电子书包完成分层性教学,学生根据自己情况,选择适合自己难 度的关卡。教师利用电子书包的监控功能可以有效选择有用的素材,然后通过学生演示进行 广播。通过学生讲解,学生互评,巩固知识的同时,也提升了自信。学生在数一数验证时, 可以让学生标上数字,培养良好的学习习惯。 (3)全是偶点情况。 老师这还有一副,有没有奇点?(没有)那就不能一笔画了吗?谁来试试?标上数字。 (互动白板直接操作) 你发现了什么?学生小结:全是偶点,都可作为起点。 设计意图:都是偶点情况比较简单,不必多花时间。让学生自己学会总结,培养严谨 的数学语言。 (4)巩固提升 找起点的方法,会了吗?换个刺激的玩法好不好? 找起点,开始?(3 题) 设计意图:利用 007 音乐制造气氛,让学生在光圈移动的过程中,快速捕捉有用信息, 判断是第一种类型还是第二种类型;第二题在熟知规则的情况下,加快光圈移动的速度;第 三题没有改变速度,增加了观察点的数量,一次一次提升捕捉难度,在这样趣味的游戏中, 学生找起点的能力得到快速提升。 (5)联系实际 你能用今天所学,解决呆头的疑惑?如果再添加一个项目,还能从大门出发一次玩遍 吗?你是设计师,你会把大门设在哪,为什么?(西沃直接现场添加项目路线) 设计意图:利用西沃 5 图形工具,直接添加项目路线,具有随机性和趣味性。通过修 改前后分别考查学生两个结论的应用情况。利用互动白板,当学生回答都是偶点时,可以让 学生自己上台通过数一数进行验证,并标上数字,给修改后的奇点判断降低了难度。这样设 计,一道题直接涵盖了本节课的所有内容,而且回扣情景。 (6)课后思考 同学们可以将答案拍成视频,发送至老师邮箱。明天中午,将优秀作品上传至群邮件, 大家一起欣赏。 设计意图:利用 QQ 平台完成课后延伸,学生可以在线下继续探索。这样做可以达到两 个目的,第一:一部分学生花一天时间验证是否能够一笔画,最后通过自己的实践发现不能 一笔画,这样就能自己发现结论三(大于两个奇点时,不能一笔画)。第二:少数学生创新 思维,通过折叠扭转的方式完成一笔画。当遇到第二种情况,应该表扬,因为这些学生勇于 打破常规,对于他们未来的发展,这是非常难得的。最后得到结论,在平面图形中,大于两 个奇点时,不能一笔画;如果进入三维空间,那么可以通过扭转折叠完成一笔画。 板书设计: 一笔画——找起点 不重复,不遗漏 2 个奇点时,只有奇点可做起点。 全是偶点,都可作为起点。查看更多