- 2021-05-25 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2012中考数学专题几何图形证明与计算题分析
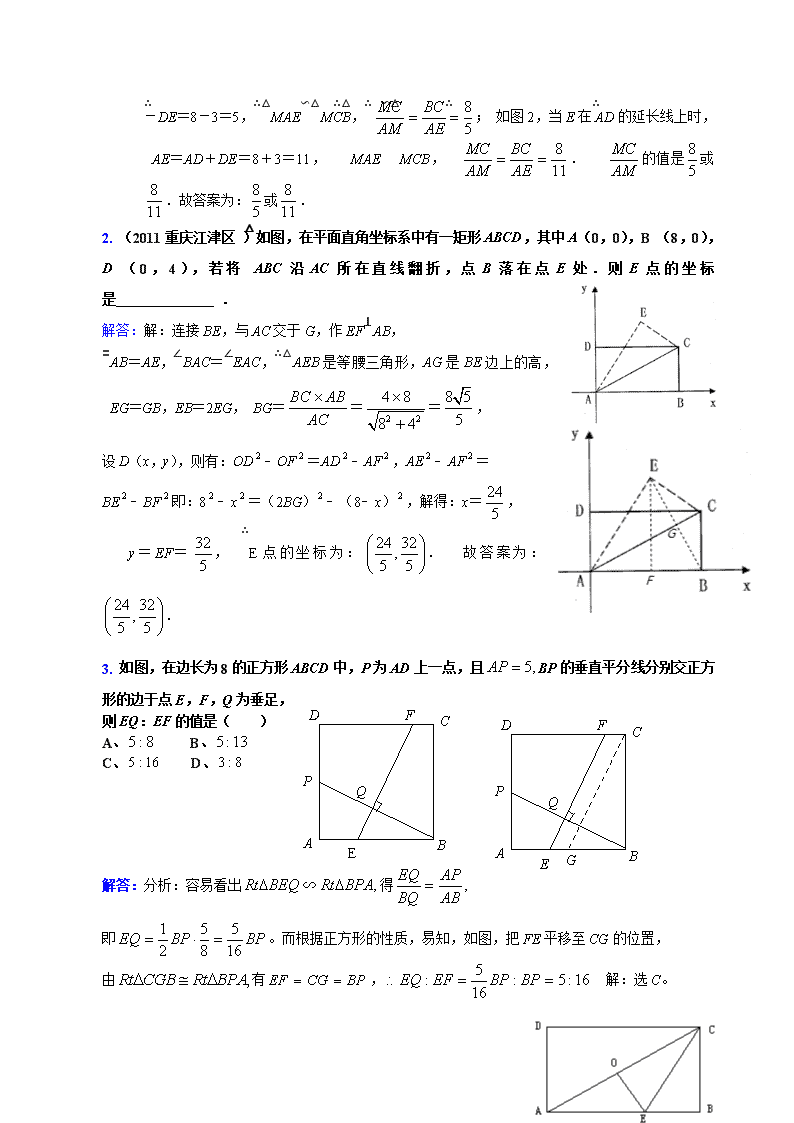
2012中考数学专题复习:几何图形证明与计算题分析 几何计算问题常见的有:求线段的长、求角的度数, 求图形的面积等。研究几何图形及其和相关的问题时,“几何计算”具有广泛的意义: 一、几何图形的大小及形状、几何图形间的位置关系,在许多时候本来就需要运用相关的数量来表示,无疑地就会涉及到几何量的计算; 二、当我们注重研究图形的动点问题,图形的变换及运动问题,在坐标系里研究图形的一些问题时,就愈是不可避免地要借助几何量的计算; 三、那些基于实际而模型化为几何图形的应用类问题,更是必须依靠几何量的计算来解决。 几何计算是深入研究图形性质和图形间关系的重要手段,是用代数形式刻划变动中图形性质的主要凭借。也就是说,许多以图形为基础的研究性问题,许多几何与代数相结合的问题,许多图形的变换及其它形式运动的问题,都是以计算为基础,为依据,为桥梁。因此几何计算问题就成了中考中不得不考的一类问题,在填空选择各类题型中都可以体现,且往往会多处出现。 几何图形线段长度计算三大方法: “勾股定理” “相似比例计算” “直角三角形中的三角函数计算” 【2011中考真题回顾与思考】 (2011深圳20题)如图9,已知在⊙O中,点C为劣弧AB上的中点,连接AC并延长至D,使CD=CA,连接DB并延长交⊙O于点E,连接AE。 (1)求证:AE是⊙O的直径; O A E C B D 图10 O A E C B D 图9 (2)如图10,连接EC,⊙O半径为5,AC的长为4,求阴影部分的面积之和。(结果保留π与根号) (1)证明:如图2,连接AB、BC, ∵点C是劣弧AB上的中点 ∴ ∴CA=CB 又∵CD=CA ∴CB=CD=CA O A E C B D 图2 ∴在△ABD中, ∴∠ABD=90° ∴∠ABE=90° ∴AE是⊙O的直径 (2)解:如图3,由(1)可知,AE是⊙O的直径 O A E C B D 图3 ∴∠ACE=90° ∵⊙O的半径为5,AC=4 ∴AE=10,⊙O的面积为25π 在Rt△ACE中,∠ACE=90°,由勾股定理,得: ∴S△ACE= ∴S阴影=S⊙O-S△ACE= (2011深圳中考21题)如图11,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,[来源:学科网]点C落在点C′的位置,BC′交AD于点G。 (1)求证:AG=C′G; (2)如图12,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM的长。 图4 A B D C C′ G 图11 A B D C C′ G G 图12 A B D C E C′ N M (1)证明:如图4,由对折和图形的对称性可知, CD=C′D,∠C=∠C′=90° 在矩形ABCD中,AB=CD,∠A=∠C=90° ∴AB= C′D,∠A=∠C′ 在△ABG和△C′DG中, ∵AB= C′D,∠A=∠C′,∠AGB=∠C′GD ∴△ABG≌△C′DG(AAS) G 图5 A B D C E C′ N M ∴AG=C′G (2)解:如图5,设EM=x,AG=y,则有: C′G=y,DG=8-y,, 在Rt△C′DG中,∠DC′G=90°,C′D=CD=6, ∴ C′G2+C′D2=DG2 即:y2+62=(8-y)2 解得: ∴C′G=cm,DG=cm 又∵△DME∽△DC′G ∴ , 即: 解得:, 即:EM=(cm) ∴所求的EM长为cm。 【典型例题分析】 1. (2011四川凉山 )已知菱形ABCD的边长是8,点E在直线AD上,若DE=3,连接BE与对角线AC相交于点M,则的值是 . 解答:解:∵菱形ABCD的边长是8,∴AD=BC=8,AD∥BC,如图1:当E在线段AD上时,∴AE=AD -DE=8-3=5,∴△MAE∽△MCB,∴; 如图2,当E在AD的延长线上时,∴AE=AD+DE=8+3=11, ∴△MAE∽△MCB,∴ . ∴ 的值是或.故答案为:或. 2. (2011重庆江津区 )如图,在平面直角坐标系中有一矩形ABCD,其中A(0,0),B (8,0),D (0,4),若将△ABC沿AC所在直线翻折,点B落在点E处.则E点的坐标是 . 解答:解:连接BE,与AC交于G,作EF⊥AB, ∵AB=AE,∠BAC=∠EAC,∴△AEB是等腰三角形,AG是BE边上的高,∴EG=GB,EB=2EG, BG===, 设D(x,y),则有:OD﹣OF=AD﹣AF,AE﹣AF= BE﹣BF即:8﹣x=(2BG)﹣(8﹣x),解得:x=, y=EF=, ∴E点的坐标为:. 故答案为:. A B C D F P E Q G A B C D F P E Q 3. 如图,在边长为8的正方形ABCD中,P为AD上一点,且BP的垂直平分线分别交正方形的边于点E,F,Q为垂足, 则EQ:EF的值是( ) A、 B、 C、 D、 解答:分析:容易看出∽得 即。而根据正方形的性质,易知,如图,把FE平移至CG的位置, 由有, 解:选C。 4. (2011•泰安)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( ) A、 B、 C、 D、6 解答:解:∵△CED是△CEB翻折而成,∴BC=CD,BE=DE,∵O是矩形ABCD的中心,∴OE是AC的垂直平分线,AC=2BC=2×3=6,∴AE=CE,在Rt△ABC中,AC2=AB2+BC2,即62=AB2+32,解得AB=3,在Rt△AOE中,设OE=x,则AE=3﹣x,AE2=AO2+OE2,即 (3﹣x)2=(3)2+32,解得x=,∴AE=EC=3﹣=2.故选A. 5. (2011•潍坊)已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O做BD垂直平分线EF,分别交AD、BC于点E、F,则AE的长为 . 解答:解:连接EB, ∵BD垂直平分EF, ∴ED=EB, 设AE=xcm,则DE=EB=(4﹣x)cm, 在Rt△AEB中, AE2+AB2=BE2, 即:x2+32=(4﹣x)2, 解得:x= 故答案为:cm. 6.如图,在中,。将绕点C逆时针旋转30°得到, 与AB相交于点D。求BD的长。 解:如图(2),作于点G,设BD=, 中, 在中,, 。 即解得。 的长为。 7.如图,在等腰梯形ABCD中,AB//CD,AD=BC,延长AB到E,使BE=DC,连结CE,若于点F,且AF平分求的值。 A B E D C F G 解答:首先,在中, 剩下的任务就是去求CF和AC之间的数量关系,如去求出CF用AC表示的代数式。 为此,去研究相应的条件:①由ABCD为等腰梯形,BECD为平行四边形(BE//CD,BE=CD),可知:AC=BD=EC;②由知 且AF平分得是等腰三角形, 设AF交BD于点G,则 ③由BG//EC,知∽, 如此一来, 当然就有。 8.如图,把一副三角板如图(1)放置,其中,,斜边把三角板DCE绕点C顺时针旋转15°得到如图(2), 这时AB与相交于点,与AB相交于点F。 (1)求的度数; (2)求线段的长; (3)若把三角形绕着点C顺时针再旋转30°得到,这时点B在的内部,外部,还是边上?证明你的判断。 解答:分析:对于(1),如图(3),设CB与相交于点G,则可通过与内角的关系,求得的值;对于(2),可先推出,并导出的长; 对于(3),设直线CB交于,应在中计算出的长,为此为基础进行判断。 解:(1)设CB与相交于点G,如图(3),则: A C B F O G 。 (2)连结, 又 。 在 (3) 。 (3)点B在内部,理由如下: 设BC(或延长线)交于点, 在, 又,即点B在内部。 9.(2009年清远)如图,已知是的直径,过点作弦的平行线,交过点的切线于点,连结. (1)求证:;(2)若,,求的长. 【答案】(1)证明: 是直径 是的切线,切点为 (2) A E D B C F G 10.(2010河南) (1)操作发现 :如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.(2)问题解决保持(1)中的条件不变,若DC=2DF,求的值; (3)类比探求:保持(1)中条件不变,若DC=nDF,求的值. 【答案】⑴同意,连接EF,则∠EGF=∠D=90°,EG=AE=ED,EF=EF. ∴ Rt△EGF≌Rt△EDF. ∴ GF=DF. ⑵ 由⑴知,GF=DF.设DF=x,BC=y,则有GF=x,AD=y. ∵DC=2DF,∴CF=x,DC=AB=BG=2x. ∴BF=BG+GF=3x. 在Rt△BCF中,BC2+CF2=BF2,即y2+x2=(3x)2. ∴y=2x,∴. ⑶由⑴知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y. ∵DC=n·DF,∴DC=AB=BG=nx. ∴CF=(n-1)x,BF=BG+GF=(n+1)x. 在Rt△BCF中,BC2+CF2=BF2,即y2+[(n-1)x]2=[(n+1)x]2. ∴y=2x.∴(或) 11.如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G. (1)求证:点F是BD中点; (2)求证:CG是⊙O的切线; (3)若FB=FE=2,求⊙O的半径. [解析] (1)证明:∵CH⊥AB,DB⊥AB, ∴△AEH∽AFB,△ACE∽△ADF ∴,∵HE=EC,∴BF=FD (2)方法一:连接CB、OC, ∵AB是直径,∴∠ACB=90°∵F是BD中点,∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO ∴∠OCF=90°,∴CG是⊙O的切线 (3)解:由FC=FB=FE得:∠FCE=∠FEC 可证得:FA=FG,且AB=BG 由切割线定理得:(2+FG)2=BG×AG=2BG2 在Rt△BGF中,由勾股定理得:BG2=FG2-BF2 由、得:FG2-4FG-12=0 解之得:FG1=6,FG2=-2(舍去) ∴AB=BG= ∴⊙O半径为2 12 . .如图,已知,以为直径,为圆心的半圆交于点,点为弧CF的中点,连接交于点,为△ABC的角平分线,且,B DA OA HA CA EA MA FA A 垂足为点. (1)求证:是半圆的切线; (2)若,,求的长. 解答:(1)证明:连接EC,∵AD⊥BE于H,∠1=∠2, ∴∠3=∠4 ∴∠4=∠5=∠3, 又∵E为弧CF中点, ∴∠6=∠7, ∵BC是直径, ∴∠E=90°, ∴∠5+∠6=90°, 又∵∠AHM=∠E=90°, ∴AD∥CE, ∴∠2=∠6=∠1, ∴∠3+∠7=90°, 又∵BC是直径, ∴AB是半圆O的切线; (2)∵,。 由(1)知,,∴. 在中,于,平分, ∴,∴. 由∽,得. ∴, ∴ 13.(2011成都)已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB.⊙O及CB的延长线相交于点E、F、G、H. (1)求证:AE=CK; (2)如果AB=a,AD=(a为大于零的常数),求BK的长: (3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长. 解答:(1)证明:∵四边形据ABCD是矩形, ∴AD=BC,∵BK⊥AC,DH∥KB, ∴∠BKC=∠AED=90°,∴△BKC≌△ADE,∴AE=CK; (2)∵AB=a,AD==BC,∴ ∵BK⊥AC,∴△BKC∽△ABC,∴, ∴, ∴BK=a,∴BK=a. (3)连接OF,∵ABCD为矩形, ∴, ∴EF=ED=×6=3,∵F是EG的中点, ∴GF=EF=3,∵△AFD≌△HBF,∴HF=FE=3+6=9, ∴GH=6,∵DH∥KB,ABCD为矩形,∴AE2=EF•ED=3×6=18,∴AE=3, ∵△AED∽△HEC,∴,∴AE=AC,∴AC= 则AO=. 14.(2011•綦江县)如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE. (1)求证:△ACD≌△BCE; (2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长. 解答:解:(1)∵△ABC与△DCE是等边三角形, ∴AC=BC,DC=EC,∠ACB=∠DCE=60°, ∴∠ACD+∠DCB=∠ECB+∠DCB=60°, ∴∠ACD=∠BCE, ∴△ACD≌△BCE(SAS); (2)过点C作CH⊥BQ于H, ∵△ABC是等边三角形,AO是角平分线, ∴∠DAC=30°, ∵△ACD≌△BCE, ∴∠QBC=∠DAC=30°, ∴CH=BC=×8=4, ∵PC=CQ=5,CH=4, ∴PH=QH=3, ∴PQ=6. 15. (2010湖北省荆门 ) 如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC∶CA=4∶3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点 (1)求证:AC·CD=PC·BC; 第15题图 (2)当点P运动到AB弧中点时,求CD的长; (3)当点P运动到什么位置时,△PCD的面积最大?并求这个最大面积S. 答案23.解:(1)∵AB为直径,∴∠ACB=90°.又∵PC⊥CD,∴∠PCD=90°. 而∠CAB=∠CPD,∴△ABC∽△PCD.∴. ∴AC·CD=PC·BC; (2)当点P运动到AB弧中点时,过点B作BE⊥PC于点E. ∵P是AB中点,∴∠PCB=45°,CE=BE=BC=2. 又∠CAB=∠CPB,∴tan∠CPB=tan∠CAB=.∴PE===. 从而PC=PE+EC=.由(1)得CD=PC= (3)当点P在AB上运动时,S△PCD=PC·CD.由(1)可知,CD=PC. ∴S△PCD=PC2.故PC最大时,S△PCD取得最大值; 而PC为直径时最大,∴S△PCD的最大值S=×52=. 16.(2010 安徽芜湖)如图,BD是⊙O的直径,OA⊥OB,M是劣弧上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于点N。 (1)求证:PM=PN; (2)若BD=4,PA=AO,过B点作BC∥MP交⊙O于C点,求BC的长. 【答案】(1)证明:连结OM,∵ MP是⊙O的切线,∴OM⊥MP ∴∠OMD +∠DMP=90° ∵OA⊥OB,∠OND +∠ODM=90° ∵∠MNP=∠OND, ∠ODN=∠OMD ∴∠DMP=∠MNP ∴PM=PN (2)解:设BC交OM于E, ∵BD=4, ∴OA=OB=2, ∴PA=OA=3 ∴PO=5 ∵BC∥MP, OM⊥MP, ∴OM⊥BC, ∴BE=BC ∵∠BOM +∠MOP=90°,在Rt△OMP中,∠MPO +∠MOP=90° ∴∠BOM=∠MPO.又∵∠BEO=∠OMP=90° ∴△OMP∽△BEO ∴ ∴,∴BE= ∴BC= E A D B C N M 17.(2010福建宁德)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM. ⑴ 求证:△AMB≌△ENB; ⑵ ①当M点在何处时,AM+CM的值最小; ②当M点在何处时,AM+BM+CM的值最小,并说明理由; ⑶ 当AM+BM+CM的最小值为时,求正方形的边长. 【答案】解:⑴∵△ABE是等边三角形, ∴BA=BE,∠ABE=60°. ∵∠MBN=60°, ∴∠MBN-∠ABN=∠ABE-∠ABN. 即∠BMA=∠NBE. 又∵MB=NB,∴△AMB≌△ENB(SAS). ⑵①当M点落在BD的中点时,AM+CM的值最小. F E A D B C N M ②如图,连接CE,当M点位于BD与CE的交点处时, AM+BM+CM的值最小. 理由如下:连接MN.由⑴知,△AMB≌△ENB, ∴AM=EN. ∵∠MBN=60°,MB=NB, ∴△BMN是等边三角形. ∴BM=MN. ∴AM+BM+CM=EN+MN+CM. 根据“两点之间线段最短”,得EN+MN+CM=EC最短 ∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长. ⑶过E点作EF⊥BC交CB的延长线于F, ∴∠EBF=90°-60°=30°. 设正方形的边长为x,则BF=x,EF=. 在Rt△EFC中, ∵EF2+FC2=EC2,∴()2+(x+x)2=. 解得,x=(舍去负值). ∴正方形的边长为.查看更多