【数学】2020届一轮复习(理)通用版考点测试40算法初步作业
考点测试40 算法初步
高考概览
考纲研读
1.了解算法的含义,了解算法的思想
2.理解程序框图的三种基本逻辑结构:顺序、条件、循环
3.了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义
一、基础小题
1.给出如图程序框图,其功能是( )
A.求a-b的值 B.求b-a的值
C.求|a-b|的值 D.以上都不对
答案 C
解析 求|a-b|的值.
2.已知一个算法:
①m=a;
②如果b
5,跳出循环,故输出A=31,而31=25-1,选B.
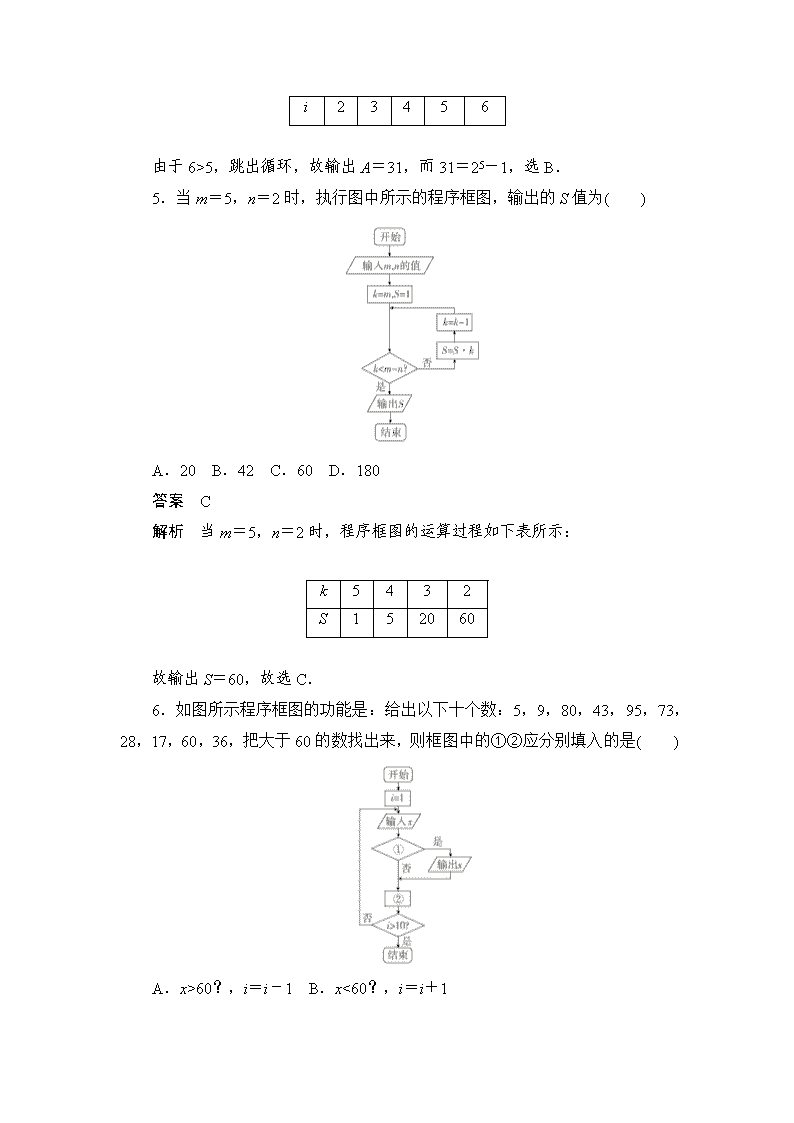
5.当m=5,n=2时,执行图中所示的程序框图,输出的S值为( )
A.20 B.42 C.60 D.180
答案 C
解析 当m=5,n=2时,程序框图的运算过程如下表所示:
k
5
4
3
2
S
1
5
20
60
故输出S=60,故选C.
6.如图所示程序框图的功能是:给出以下十个数:5,9,80,43,95,73,28,17,60,36,把大于60的数找出来,则框图中的①②应分别填入的是( )
A.x>60?,i=i-1 B.x<60?,i=i+1
C.x>60?,i=i+1 D.x<60?,i=i-1
答案 C
解析 对于A,D,由于i=i-1,则会进入死循环,而对于B,选出的数小于60.故选C.
7.在十进制中,2004=4×100+0×101+0×102+2×103,那么在五进制中数码2004折合成十进制为( )
A.29 B.254 C.602 C.2004
答案 B
解析 2004=4×50+0×51+0×52+2×53=254,故选B.
8.当x=0.2时,用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1的值时,需要做乘法和加法的次数分别是( )
A.6,6 B.5,6 C.5,5 D.6,5
答案 A
解析 由f(x)=(((a6x+a5)x+a4)x+…+a1)x+a0,所以共需要6次加法和6次乘法,故选A.
9.已知一个算法的程序框图如图所示,当输出的结果为0时,输入的实数x的值为( )
A.-3 B.-3或9
C.3或-9 D.-9或-3
答案 B
解析 本算法框图的本质为求函数y=
的零点,分情况求此分段函数的零点,易解得x=-3或x=9,故选B.
10.如图所示的程序框图的算法思路源于我国古代著名的“孙子剩余定理”,
其中“Mod(N,m)=n”表示正整数N除以正整数m后的余数为n,例如:Mod(10,3)=1.执行该程序框图,则输出的i=( )
A.23 B.38 C.44 D.58
答案 A
解析 检验选项A:i=23,Mod(23,3)=2,Mod(23,5)=3,Mod(23,7)=2,满足题意,故选A.
11.如图是“二分法”解方程的流程图,在①~④处应填写的内容分别是( )
A.f(a)f(m)<0;a=m;是;否
B.f(b)f(m)<0;b=m;是;否
C.f(b)f(m)<0;m=b;是;否
D.f(b)f(m)<0;b=m;否;是
答案 B
解析 因为题图是“二分法”解方程的流程图,
所以判断框的内容是根的存在性定理的应用,所以填f(b)f(m)<0;是,则直接验证精度,否,则先在赋值框中实现b=m的交换,再验证精度,满足精度则输出结果,结束程序,所以③处填“是”,④处填“否”,在①~④处应填写的内容分别是f(b)f(m)<0;b=m;是;否.
12.下图是用模拟方法估计圆周率π值的程序框图,P表示估计结果,则图中空白框内应填入( )
A.P= B.P=
C.P= D.P=
答案 D
解析 利用几何概型,构造一个边长为1的正方形及其内一个半径为1、圆心角为90°的扇形,易知扇形的面积S≈,又由面积公式得S=π×12≈,解得π≈,故选D.
二、高考小题
13.(2018·全国卷Ⅱ)为计算S=1-+-+…+-,设计了下面的程序框图,则在空白框中应填入( )
A.i=i+1 B.i=i+2
C.i=i+3 D.i=i+4
答案 B
解析 由S=1-+-+…+-,知程序框图先对奇数项累加,偶数项累加,最后再相减.因此在空白框中应填入i=i+2,选B.
14.(2018·北京高考)执行如图所示的程序框图,输出的s值为( )
A. B. C. D.
答案 B
解析 k=1,s=1;s=1+(-1)1×=1-=,k=2,2<3;s=+(-1)2×=+=,k=3,此时跳出循环,所以输出.故选B.
15.(2018·天津高考)阅读下边的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为( )
A.1 B.2 C.3 D.4
答案 B
解析 第一次循环T=1,i=3;第二次循环T=1,i=4;第三次循环T=2,i=5,满足条件i≥5,结束循环.故选B.
16.(2017·全国卷Ⅰ)下面程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在和两个空白框中,可以分别填入( )
A.A>1000?和n=n+1
B.A>1000?和n=n+2
C.A≤1000?和n=n+1
D.A≤1000?和n=n+2
答案 D
解析 本题求解的是满足3n-2n>1000的最小偶数n,可判断出循环结构为当型循环结构,即满足条件要执行循环体,不满足条件要输出结果,
所以判断语句应为A≤1000?,另外,所求为满足不等式的偶数解,因此中语句应为n=n+2.故选D.
17.(2017·全国卷Ⅲ)执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5 B.4 C.3 D.2
答案 D
解析 要求的是最小值,观察选项,发现选项中最小的为2,不妨将2代入检验.当输入的N为2时,第一次循环,S=100,M=-10,t=2;第二次循环,S=90,M=1,t=3,此时退出循环,输出S=90,符合题意.故选D.
18.(2017·天津高考)阅读下面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为( )
A.0 B.1 C.2 D.3
答案 C
解析 执行程序框图,输入N的值为24时,24能被3整除,执行是,N=8,8≤3不成立,继续执行循环体;8不能被3整除,执行否,N=7,7≤3不成立,继续执行循环体;7不能被3整除,执行否,N=6,6≤3不成立,继续执行循环体;6能被3整除,执行是,N=2,2≤3成立,退出循环,输出N的值为2.故选C.
19.(2017·山东高考)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )
A.0,0 B.1,1 C.0,1 D.1,0
答案 D
解析 第一次输入x=7,判断条件,4>7不成立,执行否,判断条件,7÷2=,7不能被2整除,执行否,b=3,判断条件,9>7成立,执行是,输出a=1.
第二次输入x=9,判断条件,4>9不成立,执行否,判断条件,9÷2=,9不能被2整除,执行否,b=3,判断条件,9>9不成立,执行否,判断条件,9÷3=3,9能被3整除,执行是,输出a=0.故选D.
三、模拟小题
20.(2018·衡阳二模)1927年德国汉堡大学的学生考拉兹提出一个猜想:对于每一个正整数,如果它是奇数,对它乘3再加1,如果它是偶数,对它除以2,这样循环,最终结果都能得到1.虽然该猜想看上去很简单,但有的数学家认为“该猜想任何程度的解决都是现代数学的一大进步”.
如图是根据考拉兹猜想设计的一个程序框图,则①处应填写的条件及输出的结果分别为( )
A.a是偶数? 6 B.a是偶数? 8
C.a是奇数? 5 D.a是奇数? 7
答案 D
解析 阅读考拉兹提出的猜想,结合程序框图可得①处应填写的条件是“a是奇数?”,运行情况为
a
10
5
16
8
4
2
1
i
1
2
3
4
5
6
7
所以输出的结果为i=7.故选D.
21.(2018·郑州质检一)我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
A.5 B.4 C.3 D.2
答案 B
解析 初始a=1,A=1,S=0,n=1,第一次循环:S=0+1+1=2,S小于10,进入下一次循环;第二次循环:n=n+1=2,a=,A=2,S=2++2=,S小于10,进入下一次循环;第三次循环:n=n+1=3,a=,A=4,S=++4=,S小于10,进入下一次循环;第四次循环:n=n+1=4,a=,A=8,S=++8≥10,循环结束,此时n=4,故选B.
22.(2018·合肥质检一)执行如图所示程序框图,若输入的n等于10,则输出的结果是( )
A.2 B.-3 C.- D.
答案 C
解析 a=2,i=1,满足i≤n=10,进入循环体,第一次循环:a==-3,i=2;满足i≤n=10,第二次循环:a==-,i=3;满足i≤n=10,第三次循环:a==,i=4;满足i≤n=10,第四次循环:a==2,i=5;…可看出a的取值周期性变化,且周期为4.可知当i=11时与i=3时a的取值相同,即a=-,此时,不满足i≤n=10,跳出循环体,输出a=-,故选C
.
23.(2018·贵阳模拟)我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目:“一百馒头一百僧大僧三个更无争,小僧三人分一个,大、小和尚各几丁?”如图所示的程序框图反映了此题的一个求解算法,则输出n的值为( )
A.20 B.25 C.30 D.35
答案 B
解析 开始:n=20;第一步:m=80,S=60+≠100,n=21;第二步:m=79,S=63+≠100,n=22;第三步:m=78,S=66+=92≠100,n=23;第四步:m=77,S=69+≠100,n=24;第五步:m=76,S=72+≠100,n=25;第六步:m=75,S=75+=100,此时S=100退出循环,输出n=25.故选B.
24.(2018·南昌摸底)执行如图所示的程序框图,输出n的值为( )
A.1 B.2 C.3 D.4
答案 C
解析 依据框图,可知n=1时,f(x)=(x)′=1,它是偶函数,满足f(x)=f(-x),又方程f(x)=0无解,则n=1+1=2;此时,f(x)=(x2)′=2x,不满足f(x)=f(-x),则n=2+1=3;再次循环,f(x)=(x3)′=3x2,满足f(x)=f(-x),且方程f(x)=0有解x=0,跳出循环体,则输出n的值为3,故选C.
25.(2018·深圳调研)九连环是我国一种传统的智力玩具,其构造如图1所示,要将9个圆环全部从框架上解下(或套上),无论是哪种情形,都需要遵循一定的规则.解下(或套上)全部9个圆环所需的最少移动次数可由如图2所示的程序框图得到,执行该程序框图,则输出的结果为( )
A.170 B.256 C.341 D.682
答案 C
解析 由算法框图,可知i,S的变化情况如下:
i
2
3
4
5
6
7
8
9
S
2
5
10
21
42
85
170
341
故选C.
26.(2018·邯郸摸底)我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算该木棍被截取7天后所剩的长度(单位:尺),则①②③处可分别填入的是( )
①
②
③
A
i≤7?
s=s-
i=i+1
B
i≤128?
s=s-
i=2i
C
i≤7?
s=s-
i=i+1
D
i≤128?
s=s-
i=2i
答案 B
解析 该程序框图的功能是计算木棍被截取7天后剩余部分的长度,则在程序运行过程中,应该有:第1次循环,s=1-,i=4;第2次循环,s=1--,i=8;第3次循环,s=1---,i=16;…;第7次循环,s=1---…-,i=256,此时应跳出循环体,据此判断可知在判断框①处填入“i≤128?”,执行框②处应填入“s=s-”,③处应填入“i=2i”,故选B.
本考点在近三年高考中未涉及此题型.
考点测试41 复数
高考概览
考纲研读
1.理解复数的基本概念
2.理解复数相等的充要条件
3.了解复数的代数表示法及其几何意义
4.会进行复数代数形式的四则运算
5.了解复数代数形式的加、减运算的几何意义
一、基础小题
1.设z1=2+bi,z2=a+i,当z1+z2=0时,复数a+bi=( )
A.1+i B.2+i C.3 D.-2-i
答案 D
解析 ∵z1+z2=(2+bi)+(a+i)=(2+a)+(b+1)i=0,∴∴∴a+bi=-2-i,故选D.
2.若(1+i)+(2-3i)=a+bi(a,b∈R,i是虚数单位),则a,b的值分别等于( )
A.3,-2 B.3,2 C.3,-3 D.-1,4
答案 A
解析 由于(1+i)+(2-3i)=3-2i,所以3-2i=a+bi(a,b∈R),由复数相等定义,a=3,且b=-2,故选A.
3.若复数z满足z+(3-4i)=1,则z的虚部是( )
A.-2 B.4 C.3 D.-4
答案 B
解析 z=1-(3-4i)=-2+4i,所以z的虚部是4,故选B.
4.如图,在复平面内,点A表示复数z,由图中表示z的共轭复数的点是( )
A.A B.B
C.C D.D
答案 B
解析 表示复数z的点A与表示z的共轭复数的点关于x轴对称,∴B点表示.选B.
5.已知复数z=1-i,则=( )
A.2 B.-2 C.2i D.-2i
答案 A
解析 ==2,故选A.
6.已知z=(i是虚数单位),则复数z的实部是( )
A.0 B.-1 C.1 D.2
答案 A
解析 因为z===i,所以复数z的实部为0,故选A.
7.复数=( )
A.--i B.-+i
C.-i D.+i
答案 C
解析 ==
===-i.
8.设i是虚数单位,复数为纯虚数,则实数a为( )
A.2 B.-2 C.- D.
答案 A
解析 解法一:因为=
=为纯虚数,所以2-a=0,a=2.
解法二:令=mi(m≠0),∴1+ai=(2-i)mi=m+2mi.∴∴a=2.
9.在复平面内,向量对应的复数是2+i,向量对应的复数是-1-3i,则向量对应的复数为( )
A.1-2i B.-1+2i
C.3+4i D.-3-4i
答案 D
解析 =-=-1-3i-2-i=-3-4i,故选D.
10.设z是复数,则下列命题中的假命题是( )
A.若z2≥0,则z是实数 B.若z2<0,则z是虚数
C.若z是虚数,则z2≥0 D.若z是纯虚数,则z2<0
答案 C
解析 设z=a+bi(a,b∈R),z2=a2-b2+2abi,由z2≥0,得即或所以a=0时b=0,b=0时a∈R.故z是实数,所以A为真命题;由于实数的平方不小于0,所以当z2<0时,z一定是虚数,且为纯虚数,故B为真命题;由于i2=-1<0,故C为假命题,D为真命题.
11.已知是复数z的共轭复数,若z·=2(+i),则z=( )
A.-1-i B.-1+i C.1+i D.1-i
答案 C
解析 设z=a+bi(a,b∈R),由z·=2(+i),有(a+bi)(a-bi)=2(a-bi+i),解得a=b=1,所以z=1+i,故选C.
12.在复平面内,复数z对应的点是Z(1,-2),则复数z的共轭复数=________.
答案 1+2i
解析 由复数z在复平面内的坐标有z=1-2i,所以共轭复数=1+2i.
二、高考小题
13.(2017·全国卷Ⅲ)设复数z满足(1+i)z=2i,则|z|=( )
A. B. C. D.2
答案 C
解析 解法一:∵(1+i)z=2i,∴z====1+i.∴|z|==.
解法二:∵(1+i)z=2i,∴|1+i|·|z|=|2i|,即 ·|z|=2,∴|z|=.
14.(2018·全国卷Ⅰ)设z=+2i,则|z|=( )
A.0 B. C.1 D.
答案 C
解析 因为z=+2i=+2i=+2i=i,所以|z|==1,故选C.
15.(2018·全国卷Ⅱ)=( )
A.--i B.-+i
C.--i D.-+i
答案 D
解析 ∵==,∴选D.
16.(2018·全国卷Ⅲ)(1+i)(2-i)=( )
A.-3-i B.-3+i
C.3-i D.3+i
答案 D
解析 (1+i)(2-i)=2-i+2i-i2=3+i,故选D.
17.(2018·浙江高考)复数(i为虚数单位)的共轭复数是( )
A.1+i B.1-i C.-1+i D.-1-i
答案 B
解析 ∵==1+i,∴的共轭复数为1-i.
18.(2018·北京高考)在复平面内,复数的共轭复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 D
解析 ∵==+i,∴其共轭复数为-i,又-i在复平面内对应的点,-在第四象限,故选D.
19.(2017·北京高考)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )
A.(-∞,1) B.(-∞,-1)
C.(1,+∞) D.(-1,+∞)
答案 B
解析 ∵复数(1-i)(a+i)=a+1+(1-a)i在复平面内对应的点在第二象限,∴∴a<-1.故选B.
20.(2017·山东高考)已知a∈R,i是虚数单位.若z=a+i,z·=4,则a=( )
A.1或-1 B.或-
C.- D.
答案 A
解析 ∵z=a+i,∴=a-i.又∵z·=4,∴(a+i)(a-i)=4,∴a2+3=4,∴a2=1,∴a=±1.故选A.
21.(2017·全国卷Ⅰ)设有下面四个命题:
p1:若复数z满足∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1,z2满足z1z2∈R,则z1=2;
p4:若复数z∈R,则∈R.
其中的真命题为( )
A.p1,p3 B.p1,p4 C.p2,p3 D.p2,p4
答案 B
解析 对于命题p1,设z=a+bi(a,b∈R),由==∈R,得b=0,则z∈R成立,故正确;对于命题p2,设z=a+bi(a,b∈R),由z2=(a2-b2)+2abi∈R,得a·b=0,则a=0或b=0,复数z为实数或纯虚数,故错误;对于命题p3,设z1=a+bi(a,b∈R),z2=c+di(c,d∈R),由z1·z2=(ac-bd)+(ad+bc)i∈R,得ad+bc=0,不一定有z1=2,故错误;对于命题p4,设z=a+bi(a,b∈R),则由z∈R,得b=0,所以=a∈R成立,故正确.故选B.
22.(2018·天津高考)i是虚数单位,复数=________.
答案 4-i
解析 ===4-i.
23.(2016·天津高考)已知a,b∈R,i是虚数单位.若(1+i)·(1-bi)=a,则的值为________.
答案 2
解析 由(1+i)(1-bi)=a,得1+b+(1-b)i=a,则解得所以=2.
24.(2017·浙江高考)已知a,b∈R,(a+bi)2=3+4i(i是虚数单位),则a2+b2=________,ab=________.
答案 5 2
解析 解法一:∵(a+bi)2=a2-b2+2abi,a,b∈R,
∴⇒⇒
∴a2+b2=2a2-3=5,ab=2.
解法二:由解法一知ab=2,
又|(a+bi)2|=|3+4i|=5,∴a2+b2=5.
三、模拟小题
25.(2018·郑州质检一)复数(i为虚数单位)的值为( )
A.-1-3i B.-1+3i
C.1+3i D.1-3i
答案 A
解析 ==-1-3i,故选A.
26.(2018·唐山模拟)复数z=的共轭复数为( )
A.1+2i B.1-2i C.2-2i D.-1+2i
答案 B
解析 因为z===1+2i,所以=1-2i.
27.(2018·沈阳质检一)已知i为虚数单位,复数的共轭复数在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 B
解析 因为==--i,所以其共轭复数为-+i,在复平面内所对应的点为-,,在第二象限,故选B.
28.(2018·长春质检二)已知复数z=1+i(i是虚数单位),则z2+z=( )
A.1-2i B.1+3i C.1-3i D.1+2i
答案 B
解析 z2+z=(1+i)2+1+i=1+2i+i2+1+i=1+3i.故选B.
29.(2018·湖北八市联考)设复数z=(i为虚数单位),则下列命题错误的是( )
A.|z|=
B.=1-i
C.z的虚部为i
D.z在复平面内对应的点位于第一象限
答案 C
解析 依题意,有z==1+i,则其虚部为1,故选C.
30.(2018·石家庄质检二)已知复数z满足zi=i+m(i为虚数单位,m∈R),若z的虚部为1,则复数z在复平面内对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 A
解析 依题意,设z=a+i(a∈R),则由zi=i+m,得ai-1=i+m,从而故z=1+i,在复平面内对应的点为(1,1),在第一象限,故选A.
31.(2018·太原模拟)设复数z满足=i(i为虚数单位),则z的共轭复数为( )
A.i B.-i C.2i D.-2i
答案 A
解析 由=i,整理得(1+i)z=1-i,z===-i,所以z的共轭复数为i.故选A.
32.(2018·南昌一模)欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”,根据欧拉公式可知,ei表示的复数位于复平面内的( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 A
解析 由欧拉公式ei=cos+isin=+i,所以ei表示的复数位于复平面内的第一象限.选A.
33.(2018·衡阳三模)若复数z满足z+i=(i为虚数单位),则复数z的虚部为( )
A.2 B.2i C.-2 D.-2i
答案 C
解析 由z+i=,得z+i=-i,z=-2i,故复数z的虚部为-2,故选C.
34.(2018·青岛模拟)在复平面内,设复数z1,z2对应的点关于虚轴对称,z1=1+2i(i是虚数单位),则z1z2=( )
A.5 B.-5 C.-1-4i D.-1+4i
答案 B
解析 由题意z2=-1+2i,所以z1z2=(1+2i)(-1+2i)=-1+4i2=-5.故选B.
一、高考大题
本考点在近三年高考中未涉及此题型.
二、模拟大题
1.(2018·成都诊断)已知关于t的一元二次方程t2+(2+i)t+2xy+(x-y)i=0(x,y∈R).
(1)当方程有实根时,求点(x,y)的轨迹方程;
(2)求方程的实根的取值范围.
解 (1)设实根为m,则m2+(2+i)m+2xy+(x-y)i=0,
即(m2+2m+2xy)+(m+x-y)i=0.
根据复数相等的充要条件得
由②得m=y-x,代入①得(y-x)2+2(y-x)+2xy=0,
即(x-1)2+(y+1)2=2.
故点(x,y)的轨迹方程为(x-1)2+(y+1)2=2.
(2)由(1)知点(x,y)的轨迹是一个圆,圆心为(1,-1),半径r=,
设方程的实根为m,
则直线m+x-y=0与圆(x-1)2+(y+1)2=2有公共点,
所以≤,即|m+2|≤2,即-4≤m≤0.
故方程的实根的取值范围是[-4,0].
2.(2018·九江高二质检)已知M={1,(m2-2m)+(m2+m-2)i},P={-1,1,4i},若M∪P=P,求实数m的值.
解 ∵M∪P=P,∴M⊆P.
即(m2-2m)+(m2+m-2)i=-1或(m2-2m)+(m2+m-2)i=4i.
当(m2-2m)+(m2+m-2)i=-1时,
有解得m=1;
当(m2-2m)+(m2+m-2)i=4i时,
有解得m=2.
综上可知m=1或m=2.