- 2021-05-22 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学文科模拟题1及答案
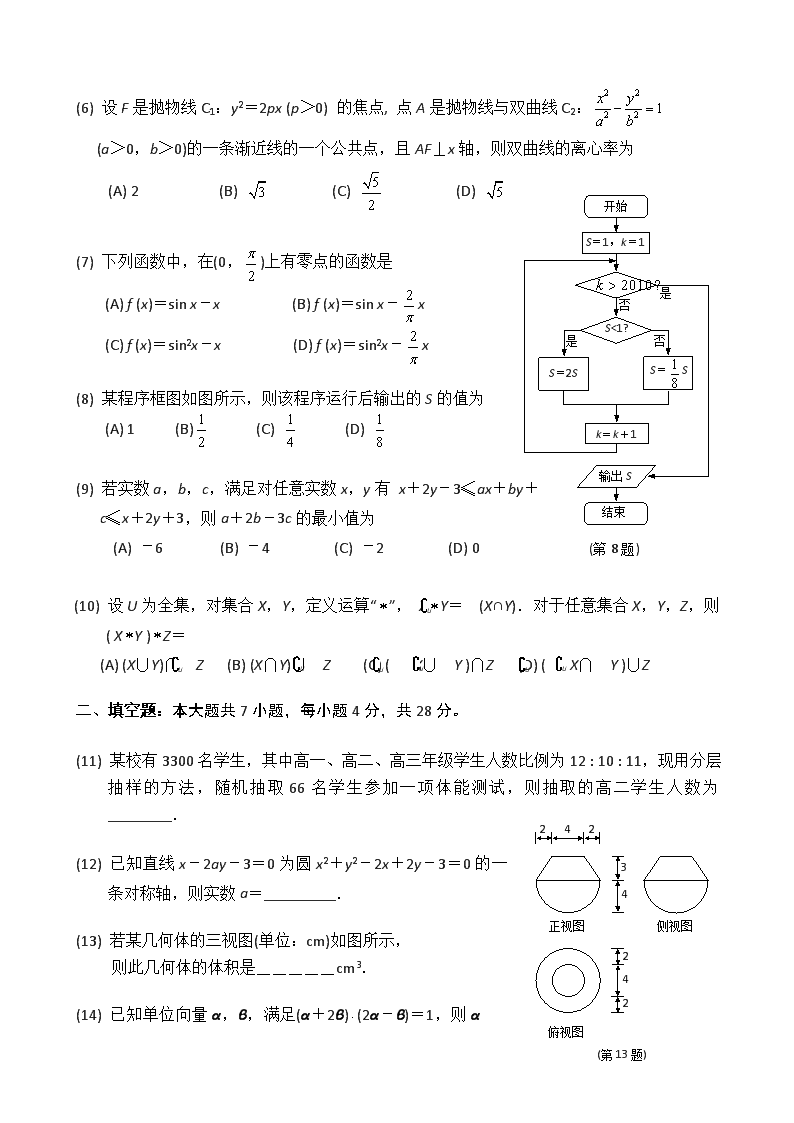
2011年高考数学[文科]模拟题1 参考公式: 球的表面积公式 S = 4R2 球的体积公式 其中R表示球的半径 锥体的体积公式 V = Sh 其中S表示锥体的底面积,h表示锥体的高 柱体的体积公式 V = Sh 其中S表示柱体的底面积,h表示柱体的高 台体的体积公式 其中S1,S2分别表示台体的上、下底面积, h表示台体的高 如果事件A,B互斥,那么P(A+B) = P(A) + P(B) 一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。 (1) 已知函数f (x)= 则 f (0)+f (-1)= (A) 8 (B) (C) 2 (D) (2) 已知i为虚数单位,则= (A) 1+3i (B) 1-3i (C) 3-i (D) 3+i (3) “sin x=1”是 “cos x=0”的 (A) 充分而不必要条件 (B) 必要而不充分条件 (C) 充分必要条件 (D) 既不充分也不必要条件 (4) 在等比数列{an}中,若a2+a3=4,a4+a5=16,则a8+a9= (A) 128 (B) -128 (C) 256 (D) -256 (5) 设l,m是不同的直线,α,β,γ是不同的平面,则下列命题正确的是 (A) 若l⊥m,m⊥α,则l⊥α或 l∥α (B) 若l⊥γ,α⊥γ,则l∥α或 lα (C) 若l∥α,m∥α,则l∥m或 l与m相交 (D) 若l∥α,α⊥β,则l⊥β或 lβ (6) 设F是抛物线C 1:y2=2px (p>0) 的焦点, 点A是抛物线与双曲线C2: (a>0,b>0)的一条渐近线的一个公共点,且AF⊥x轴,则双曲线的离心率为 开始 (A) 2 (B) (C) (D) S=1,k=1 是 (7) 下列函数中,在(0,)上有零点的函数是 S<1? 否 (A) f (x)=sin x-x (B) f (x)=sin x-x 否 是 S=S S=2S (C) f (x)=sin2x-x (D) f (x)=sin2x-x (8) 某程序框图如图所示,则该程序运行后输出的S的值为 k=k+1 (A) 1 (B) (C) (D) 输出S 结束 (9) 若实数a,b,c,满足对任意实数x,y有 x+2y-3≤ax+by+c≤x+2y+3,则a+2b-3c的最小值为 (第8题) (A) -6 (B) -4 (C) -2 (D) 0 U U U U U U U (10) 设U为全集,对集合X,Y,定义运算“”, XY= (X∩Y).对于任意集合X,Y,Z,则 ( XY )Z= (A) (X∪Y)∩ Z (B) (X∩Y)∪ Z (C) ( X∪ Y )∩Z (D) ( X∩ Y )∪Z 二、填空题:本大题共7小题,每小题4分,共28分。 242 3 4 2 2 4 正视图 俯视图 侧视图 (第13题) (11) 某校有3300名学生,其中高一、高二、高三年级学生人数比例为12 : 10 : 11,现用分层抽样的方法,随机抽取66名学生参加一项体能测试,则抽取的高二学生人数为________. (12) 已知直线x-2ay-3=0为圆x2+y2-2x+2y-3=0的一条对称轴,则实数a=_________. (13) 若某几何体的三视图(单位:cm)如图所示, 则此几何体的体积是_____cm3. (14) 已知单位向量α,β,满足(α+2β)(2α-β)=1,则α 与β的夹角的余弦值为______. (第15题) H G F E D C B A (15) 如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为________. (16) 定义在R上的偶函数f (x)满足f (x+1)=f (1-x).若当0≤x<1时,f (x)=2x,则f (log26)=________. (17) 甲、乙两队各有3个队员,已知甲队的每个队员分别与乙队的每个队员各握手一次 (同队的队员之间不握手),则在任意的两次握手中恰有3个队员参与的概率为_______. 三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。 (18) (本题满分14分)在锐角△ABC中,cos B+cos (A-C)=sin C. (Ⅰ) 求角A的大小; (Ⅱ) 当BC=2时,求△ABC面积的最大值. (19) (本题满分14分) 设首项为a1,公差为d的等差数列{an}的前n项和为Sn. 已知a7=-2,S5=30. (Ⅰ) 求a1及d; (Ⅱ) 若数列{bn}满足an= (n∈N*), 求数列{bn}的通项公式. B1 D A B C C1 D1 (第20题) O (20) (本题满分14分) 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=,AD=3,BB1=1. (Ⅰ) 设O是线段BD的中点, 求证:C1O∥平面AB1D1; (Ⅱ) 求直线AB1与平面ADD1所成的角. (21) (本题满分15分) 已知实数a满足1<a≤2,设函数f (x)=x3-x2+ax. (Ⅰ) 当a=2时,求f (x)的极小值; (Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同, 求证:g(x)的极大值小于等于10. x y O (第22题) B A D B1 A1 D1 (22) (本题满分15分) 已知直线l1:x=my与抛物线C:y2=4x交于O (坐标原点),A两点,直线l2:x=my+m 与抛物线C交于B,D两点. (Ⅰ) 若 | BD | = 2 | OA |,求实数m的值; (Ⅱ) 过A,B,D分别作y轴的垂线,垂足分别为A1,B1,D1.记S1,S2分别为三角形OAA1和四边形BB1D1D的面积, 求的取值范围. 说明: 一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分参考制订相应的评分细则。 二、对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容与难度,可视影响的程度决定后续部分的给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分。 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。 四、只给整数分数。选择题和填空题不给中间分(第11题除外)。 五、未在规定区域内答题,每错一个区域扣卷面总分1分。 2011年高考数学[文科]模拟题1参考答案 一、选择题:本题考查基本知识和基本运算。每小题5分,满分50分。 (1) C (2) A (3) A (4) C (5) B (6) D (7) D (8) C (9) B (10) B 二、填空题: 本题考查基本知识和基本运算。每小题4分,满分28分。 (11) 20 (12) 1 (13) (14) (15) (16) (17) 三、解答题:本大题共5小题,共72分。 (18) 本题主要考查三角变换、余弦定理、三角形面积公式、均值不等式等基础知识,同时考查三角运算求解能力。满分14分。 (Ⅰ) 解:因为cos B+cos (A-C)=sin C, 所以-cos (A+C)+cos (A-C)=sin C,得 2sin A sin C=sinC, 故sin A=. 因为△ABC为锐角三角形, 所以A=60°.………………………………………7分 (Ⅱ) 解:设角A,B,C所对的边分别为a,b,c. 由题意知 a=2, 由余弦定理得 4=b2+c2-2bccos60°=b2+c2-bc≥bc, 所以△ABC面积=bcsin60°≤, 且当△ABC为等边三角形时取等号, 所以△ABC面积的最大值为. ………………………14分 (19) 本题主要考查等差数列通项、求和公式、数列前n项和与通项的关系等基础知识,同时考查运算求解能力及抽象概括能力。满分14分。 (Ⅰ) 解:由题意可知 得 ………………………………………6分 (Ⅱ) 解:由(Ⅰ)得 an=10+(n-1)(-2)=12-2n, 所以 b1+2b2+3b3+…+nbn=nan=n(12-2n), 当n=1时,b1=10, 当n≥2时,b1+2b2+3b3+…+(n-1)bn-1=(n-1)[12-2(n-1)], 所以nbn= n(12-2n)-(n-1)[12-2(n-1)]=14-4n, 故bn=-4. 当n=1时也成立. 所以bn=-4 (n∈N*). ……………………………14分 (20) 本题主要考查空间线线、线面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。满分14分。 A1 B1 D A B C C1 D1 (第20题) O F E (Ⅰ) 证明:取B1D1的中点E,连结C1E,OA,则A,O,C共线,且 C1E=OA, 因为BCD-B1C1D1为三棱柱, 所以平面BCD∥平面B1C1D1, 故C1E∥OA, 所以C1EAO为平行四边形, 从而C1O∥EA. 又因为C1O平面AB1D1, EA平面AB1D1, 所以C1O∥平面AB1D1.………………………………………………7分 (Ⅱ) 解:过B1在平面B1C1D1内作B1A1∥C1D1,使B1A1=C1D1. 连结A1D1,AA1. 过B1作A1D1的垂线,垂足为F, 则B1F⊥平面ADD1, 所以∠B1AF为AB1与平面ADD1所成的角. 在Rt△A1B1F中,B1F=A1B1sin 60°=. 在Rt△AB1F中,AB1=, 故sin∠B1AF ==. 所以∠B1AF=45°. 即直线AB1与平面ADD1所成角的大小为45°. …………………14分 (21) 本题主要考查函数的极值概念、导数运算法则、导数应用等基础知识,同时考查抽象概括、运算求解能力和创新意识。满分15分。 (Ⅰ)解:当a=2时,f ′(x)=x2-3x+2=(x-1)(x-2). 列表如下: x (-,1) 1 (1,2) 2 (2,+) f ′(x) + 0 - 0 + f (x) 单调递增 极大值 单调递减 极小值 单调递增 所以,f (x)的极小值为f (2)=.…………………………………6分 (Ⅱ) 解:f ′(x)=x2-(a+1)x+a=(x-1)(x-a). 由于a>1, 所以f (x)的极小值点x=a,则g(x)的极小值点也为x=a. 而g ′ (x)=12x2+6bx-6(b+2)=6(x-1)(2x+b+2), 所以, 即b=-2(a+1). 又因为1<a≤2, 所以 g(x)极大值=g(1) =4+3b-6(b+2) =-3b-8 =6a-2 ≤10. 故g(x)的极大值小于等于10.…………………………15分 (22) 本题主要考查直线与抛物线的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力。满分15分。 (Ⅰ) 解: 设B(x1,y1), D(x2,y2), 由 得 , 由Δ,得或, 且y1+y2=4m, y1y2=-4m. 又由 得 y2-4my=0, 所以y=0或4m. 故A (4m2,4m). 由 | BD |=2 | OA |,得 (1+m2)(y1-y2)2=4 (16m4+16m2), 而 (y1-y2)2=16m2+16m, 故m=. ………………………… 6分 (Ⅱ) 解: 由(Ⅰ)得 x1+x2=m(y1+y2)+2m=4m2+2m. 所以= = = =. 令=t, 因为或, 所以-1<t<0或t>0. 故 =, 所以 0<<1 或 >1, 即 0<<1 或 >1. 所以,的取值范围是(0,1)∪(1,+∞). ………………………15分查看更多