2020年山东省济南市市中区育英中学中考数学模拟试卷(三)
2020年山东省济南市市中区育英中学中考数学模拟试卷(三)
一、选择题(共12小题,每小题3分,满分36分)
1. −56的绝对值是( )
A.−65 B.65 C.56 D.−56
2. 为应对疫情,许多企业跨界抗疫,生产口罩.截至2月29日,全国口罩日产量达到116000000只.将116000000用科学记数法表示应为( )
A.116×106 B.11.6×107 C.1.16×107 D.1.16×108
3. 如图所示,正三棱柱的俯视图是( )
A. B. C. D.
4. 已知直线l1 // l2,将一块含30∘角的直角三角板ABC按如图方式放置,若∠1=85∘,则∠2等于( )
A.35∘ B.45∘ C.55∘ D.65∘
5. 下列式子运算正确的是( )
A.t2+t4=t6 B.(3x2)3=9x5
C.m8÷m4=m2 D.(x−12)2=x2−x+14
6. 如表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.众数是177 B.平均数是170 C.中位数是173.5 D.方差是135
7. 下列图案中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
8. 若关于x的一元二次方程x2−4x+c=0有实数根,则常数c的值不可能为( )
A.−4 B.4 C.−16 D.16
9. 如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45∘,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60∘和30∘,则该电线杆PQ的高度( )
A.6+23 B.6+3 C.10−3 D.8+3
10. 如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连接AE、AF.若AB=6,∠B=60∘,则阴影部分的面积为( )
A.93−3π B.93−2π C.183−9π D.183−6π
11. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若AE=2,AD=6,则两个三角形重叠部分的面积为(
第25页 共28页 ◎ 第26页 共28页
)
A.2 B.3−2 C.3−1 D.3−3
12. 二次函数y=x2+mx−n的对称轴为x=2.若关于x的一元二次方程x2+mx−n=0在−1
0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=210.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=kx(x>0)的图象于点C.
①连接AC,求△ABC的面积;
②在图上连接OC交AB于点D,求ADBD的值.
【问题探究】
(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90∘,点B,D,E在同一直线上,连接AD,BD.
①请探究AD与BD之间的位置关系:________;
②若AC=BC=10,DC=CE=2,则线段AD的长为________;
【拓展延伸】
(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90∘,AC=21,BC=7,CD=3,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0∘≤α<360∘),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.
如图1,直线y=−43x+n交x轴于点A,交y轴于点C(0, 4),抛物线y=23x2+bx+c经过点A,交y轴于点B(0, −2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
1求抛物线的解析式;
2当△BDP为等腰直角三角形时,求线段PD的长;
3如图2,将△BDP绕点B逆时针旋转,得到△BD′P′,且旋转角∠PBP′=∠OAC,当点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
第25页 共28页 ◎ 第26页 共28页
参考答案与试题解析
2020年山东省济南市市中区育英中学中考数学模拟试卷(三)
一、选择题(共12小题,每小题3分,满分36分)
1.
【答案】
C
【考点】
绝对值
【解析】
直接利用绝对值的定义得出答案.
【解答】
−56的绝对值是:56.
2.
【答案】
D
【考点】
科学记数法--表示较大的数
【解析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】
将116000000用科学记数法表示应为1.16×108.
3.
【答案】
B
【考点】
简单几何体的三视图
【解析】
正三棱柱从上面看到的图形即俯视图.
【解答】
俯视图是从上面看所得到的图形,看见的棱用实线表示,看不见的用虚线表示,
4.
【答案】
D
【考点】
平行线的性质
【解析】
利用对顶角相等及三角形内角和定理,可求出∠4的度数,由直线l1 // l2,利用“两直线平行,内错角相等”可求出∠2的度数.
【解答】
解:如图,
∵ 直线l1 // l2,
∴ ∠1=∠5=∠3=85∘,
又∵ ∠A+∠3+∠4=180∘,∠A=30∘,
∴ ∠4=65∘,
∴ ∠2=∠4=65∘.
故选D.
5.
【答案】
D
【考点】
同底数幂的除法
完全平方公式
幂的乘方与积的乘方
合并同类项
【解析】
分别根据合并同类项法则,积的乘方运算法则,同底数幂的除法法则以及完全平方公式逐一判断即可.
【解答】
A.t2与t4不是同类项,所以不能合并,故本选项不合题意;
B.(3x2)3=9x6,故本选项不合题意;
C.m8÷m4=m4,故本选项不合题意;
D.(x−12)2=x2−x+14,正确.
6.
【答案】
D
【考点】
加权平均数
中位数
众数
方差
【解析】
根据平均数、方差、中位数和众数的定义分别进行解答,即可求出答案.
【解答】
A、这组数据中177出现次数最多,即众数为177,此选项正确;
B、这组数据的平均数是:(140+160+169+170×2+177×3+180×2)÷10=170,此选项正确;
C、∵ 共有10个数,
∴
第25页 共28页 ◎ 第26页 共28页
中位数是第5个和6个数的平均数,
∴ 中位数是(170+177)÷2=173.5;此选项正确;
D、方差=110[(140−170)2+(160−170)2+(169−170)2+2×(170−170)2+3×(177−170)2+2×(180−170)2]=134.8;此选项错误;
7.
【答案】
A
【考点】
中心对称图形
轴对称图形
【解析】
根据轴对称图形与中心对称图形的概念求解.
【解答】
A、是中心对称图形,是轴对称图形,故此选项符合题意;
B、不是中心对称图形,是轴对称图形,故此选项不合题意;
C、是中心对称图形,不是轴对称图形,故此选项不符合题意;
D、不是中心对称图形,不是轴对称图形,故此选项不合题意;
8.
【答案】
D
【考点】
根的判别式
【解析】
利用判别式的意义得到△=(−4)2−4c≥0,解不等式得到c的范围,然后对各选项进行判断.
【解答】
根据题意得△=(−4)2−4c≥0,
解得c≤4.
9.
【答案】
A
【考点】
解直角三角形的应用-仰角俯角问题
【解析】
延长PQ交直线AB于点E,设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE−BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
【解答】
∵ ∠PBE=60∘
∴ ∠BPE=30∘
在直角△BPE中,BE=33PE=33x米,
∵ AB=AE−BE=6米,
则x−33x=6,
解得:x=9+33.
则BE=(33+3)米.
在直角△BEQ中,QE=33BE=33(33+3)=(3+3)米.
∴ PQ=PE−QE=9+33−(3+3)=6+23(米).
答:电线杆PQ的高度是6+23米.
故选:A.
10.
【答案】
A
【考点】
菱形的性质
扇形面积的计算
等边三角形的性质与判定
【解析】
连接AC,根据菱形的性质求出∠BCD和BC=AB=6,求出AE长,再根据三角形的面积和扇形的面积求出即可.
【解答】
连接AC,
∵ 四边形ABCD是菱形,
∴ AB=BC=6,
∵ ∠B=60∘,E为BC的中点,
∴ CE=BE=3=CF,△ABC是等边三角形,AB // CD,
∵ ∠B=60∘,
∴ ∠BCD=180∘−∠B=120∘,
由勾股定理得:AE=62−32=33,
∴ S△AEB=S△AEC=12×6×33×12=4.53=S△AFC,
∴ 阴影部分的面积S=S△AEC+S△AFC−S扇形CEF=4.53+4.53−120π×32360=93−3π,
11.
【答案】
D
【考点】
全等三角形的性质
等腰直角三角形
【解析】
本题考查全等三角形的判定和性质、等腰直角三角形的性质、勾股定理、角平分线的性质等知识.
【解答】
第25页 共28页 ◎ 第26页 共28页
解:如图,设AB交CD于O,连结BD,作OM⊥DE于M,ON⊥BD于N.
∵ ∠ECD=∠ACB=90∘,
∴ ∠ECA=∠DCB,
∵ CE=CD,CA=CB,
∴ △ECA≅△DCB,
∴ ∠E=∠CDB=45∘,AE=BD=2,
∵ ∠EDC=45∘,
∴ ∠ADB=∠ADC+∠CDB=90∘,
在Rt△ADB中,AB=AD2+DB2=22,
∴ AC=BC=2,
∴ S△ABC=12×2×2=2,
∵ OD平分∠ADB,OM⊥DE于M,ON⊥BD于N,
∴ OM=ON,
∵ S△AODS△DOB=OAOB=12⋅AD⋅OM12⋅DB⋅ON=62=3,
∴ S△AOC=2×33+1=3−3.
故选D.
12.
【答案】
C
【考点】
抛物线与x轴的交点
二次函数的性质
【解析】
根据对称轴求出m的值,从而得到x=−1、6时的函数y=x2−4x值,再根据一元二次方程x2+mx−n=0在−1−4,
所以不等式组的解集为x≥1,
所以最小整数解是1.
【考点】
一元一次不等式组的整数解
解一元一次不等式组
【解析】
首先解不等式组中的每个不等式,然后确定两个不等式的解集的公共部分,即可确定不等式组的解集.然后即可确定最小的整数解即可.
【解答】
2x+3≥5x−42−4,
所以不等式组的解集为x≥1,
所以最小整数解是1.
【答案】
证明:∵ 四边形ABCD是平行四边形,
∴ AB // CD,AB=CD,
∴ ∠ABE=∠CDF,
在△ABE和△DCF中,
∠BAE=∠DCFAB=CD∠ABE=∠CDF
∴ △ABE≅△DCF(ASA),
∴ BE=DF,
∴ BE+EF=DF+EF,
即BF=DE.
【考点】
全等三角形的性质与判定
平行四边形的性质
【解析】
欲证明BF=DE,只要证明△ABE≅△DCF即可.
【解答】
证明:∵ 四边形ABCD是平行四边形,
∴ AB // CD,AB=CD,
∴ ∠ABE=∠CDF,
在△ABE和△DCF中,
∠BAE=∠DCFAB=CD∠ABE=∠CDF
∴ △ABE≅△DCF(ASA),
∴ BE=DF,
∴ BE+EF=DF+EF,
即BF=DE.
【答案】
原计划每天制作12件手工品
【考点】
分式方程的应用
【解析】
关键描述语为:“提前10天完成任务”;等量关系为:原计划天数=实际生产天数+10.
【解答】
设原计划每天制作x件手工品,
可得:360x=3601.5x+10,
解得:x=12,
经检验x=12是原方程的解,
【答案】
证明:
∵ CD是⊙O的切线,切点为C,
∴ OC⊥DE,
∵ BE⊥DE,
∴ CO // BE,
∴ ∠OCB=∠EBC,
又∵ 且OC=OB,
∴ ∠OCB=∠OBC;
∴ ∠OBC=∠EBC,
∴ BC平分∠ABE;
∵ AB是⊙O的直径,
∴ ∠ACB=90∘,
∵ ∠A=60∘,
∴ ∠ABC=30∘,
∵ ⊙O的半径为2,
∴ AB=4,
∴ AC=2,
∴ BC=AB2−AC2=23,
∵ BC平分∠ABE,
∴ ∠CBE=30∘,
∴ CE=12BC=3.
【考点】
切线的性质
勾股定理
第25页 共28页 ◎ 第26页 共28页
含30度角的直角三角形
【解析】
(1)连接OC,利用切线的性质和已知条件证明BE // OC,进而得到内错角相等,再利用圆的半径相等得到相等的角即可证明BC平分∠ABE;
(2)由圆周角定理可知∠ACB=90∘,所以∠ABC=30∘,由(1)可知∠CBE=30∘,利用勾股定理和在直角三角形中,30∘角所对的直角边等于斜边的一半即可求出CE的长.
【解答】
证明:
∵ CD是⊙O的切线,切点为C,
∴ OC⊥DE,
∵ BE⊥DE,
∴ CO // BE,
∴ ∠OCB=∠EBC,
又∵ 且OC=OB,
∴ ∠OCB=∠OBC;
∴ ∠OBC=∠EBC,
∴ BC平分∠ABE;
∵ AB是⊙O的直径,
∴ ∠ACB=90∘,
∵ ∠A=60∘,
∴ ∠ABC=30∘,
∵ ⊙O的半径为2,
∴ AB=4,
∴ AC=2,
∴ BC=AB2−AC2=23,
∵ BC平分∠ABE,
∴ ∠CBE=30∘,
∴ CE=12BC=3.
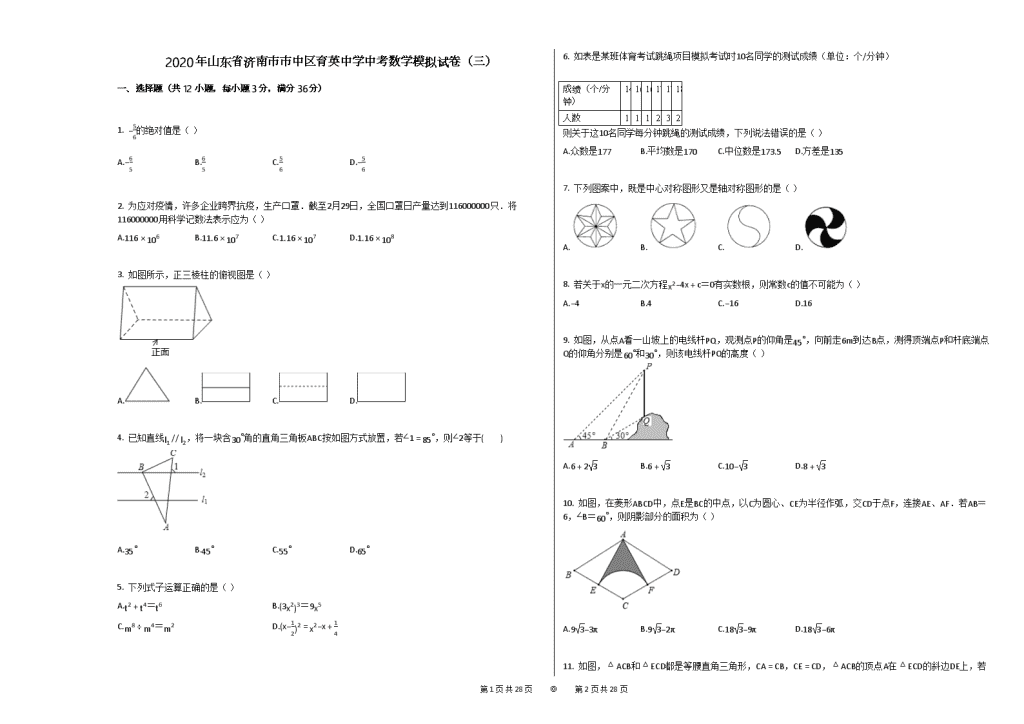
【答案】
50,108
因为阅读5本的有2人,阅读8本的有3人,所以可设A、B表示阅读5本的学生,C、D、E表示阅读8本的学生,画树状图得:
∵ 共有20种等可能的结果,抽得这两名学生阅读的本数均为8本的有6种情况,
∴ P(两名学生都读8本)=6÷20=310.
【考点】
折线统计图
扇形统计图
列表法与树状图法
【解析】
(1)由阅读中外名著本数为6本的有30人,占60%,可求得总人数;用阅读中外名著本数为7本的人数除以总人数得到其所占的百分比,再乘以360∘,则可求得扇形的圆心角的度数;用总人数减去阅读本数为5、6、7本的人数,得到阅读本数为8本的人数,即可补全折线图;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与这两名学生阅读的本数均为8的情况,再利用概率公式求解即可求得答案.
【解答】
该班学生共有30÷60%=50名,
圆心角的度数是15÷50×360∘=108∘,
50−2−30−15=3(人)
补全如图:
因为阅读5本的有2人,阅读8本的有3人,所以可设A、B表示阅读5本的学生,C、D、E表示阅读8本的学生,画树状图得:
∵ 共有20种等可能的结果,抽得这两名学生阅读的本数均为8本的有6种情况,
∴ P(两名学生都读8本)=6÷20=310.
【答案】
过点A作AH⊥x轴,垂足为点H,AH交OC于点M,如图所示.
∵
第25页 共28页 ◎ 第26页 共28页
OA=AB,AH⊥OB,
∴ OH=BH=12OB=2,
∴ AH=OA2−OH2=40−4=6,
∴ 点A的坐标为(2, 6).
∵ A为反比例函数y=kx图象上的一点,
∴ k=2×6=12;
①∵ BC⊥x轴,OB=4,点C在反比例函数y=12x上,
∴ BC=124=3.
∵ AH⊥OB,
∴ AH // BC,
∴ 点A到BC的距离=BH=2,
∴ S△ABC=12×3×2=3;
②∵ BC⊥x轴,OB=4,点C在反比例函数y=12x上,
∴ BC=124=3.
∵ AH // BC,OH=BH,
∴ MH=12BC=32,
∴ AM=AH−MH=92.
∵ AM // BC,
∴ △ADM∽△BDC,
∴ ADDB=AMBC=32.
【考点】
反比例函数综合题
【解析】
(1)过点A作AH⊥x轴,垂足为点H,AH交OC于点M,利用等腰三角形的性质可得出DH的长,利用勾股定理可得出AH的长,进而可得出点A的坐标,再利用反比例函数图象上点的坐标特征即可求出k值;
(2)①由三角形面积公式可求解;
②由OB的长,利用反比例函数图象上点的坐标特征可得出BC的长,利用三角形中位线定理可求出MH的长,进而可得出AM的长,由AM // BC可得出△ADM∽△BDC,利用相似三角形的性质即可求出ADDB的值.
【解答】
过点A作AH⊥x轴,垂足为点H,AH交OC于点M,如图所示.
∵ OA=AB,AH⊥OB,
∴ OH=BH=12OB=2,
∴ AH=OA2−OH2=40−4=6,
∴ 点A的坐标为(2, 6).
∵ A为反比例函数y=kx图象上的一点,
∴ k=2×6=12;
①∵ BC⊥x轴,OB=4,点C在反比例函数y=12x上,
∴ BC=124=3.
∵ AH⊥OB,
∴ AH // BC,
∴ 点A到BC的距离=BH=2,
∴ S△ABC=12×3×2=3;
②∵ BC⊥x轴,OB=4,点C在反比例函数y=12x上,
∴ BC=124=3.
∵ AH // BC,OH=BH,
∴ MH=12BC=32,
∴ AM=AH−MH=92.
∵ AM // BC,
∴ △ADM∽△BDC,
∴ ADDB=AMBC=32.
【答案】
AD⊥BD,4
若点D在BC右侧,
如图,过点C作CF⊥AD于点F,
∵
第25页 共28页 ◎ 第26页 共28页
∠ACB=∠DCE=90∘,AC=21,BC=7,CD=3,CE=1.
∴ ∠ACD=∠BCE,ACBC=3=CDCE
∴ △ACD∽△BCE
∴ ∠ADC=∠BEC,
∵ CD=3,CE=1
∴ DE=DC2+CE2=2
∵ ∠ADC=∠BEC,∠DCE=∠CFD=90∘
∴ △DCE∽△CFD,
∴ DEDC=DCCF=CEDF
即23=3CF=1DF
∴ CF=32,DF=32
∴ AF=AC2−CF2=532
∴ AD=DF+AF=33
若点D在BC左侧,
∵ ∠ACB=∠DCE=90∘,AC=21,BC=7,CD=3,CE=1.
∴ ∠ACD=∠BCE,ACBC=3=CDCE
∴ △ACD∽△BCE
∴ ∠ADC=∠BEC,
∴ ∠CED=∠CDF
∵ CD=3,CE=1
∴ DE=DC2+CE2=2
∵ ∠CED=∠CDF,∠DCE=∠CFD=90∘
∴ △DCE∽△CFD,
∴ DEDC=DCCF=CEDF
即23=3CF=1DF
∴ CF=32,DF=32
∴ AF=AC2−CF2=532
∴ AD=AF−DF=23
【考点】
几何变换综合题
【解析】
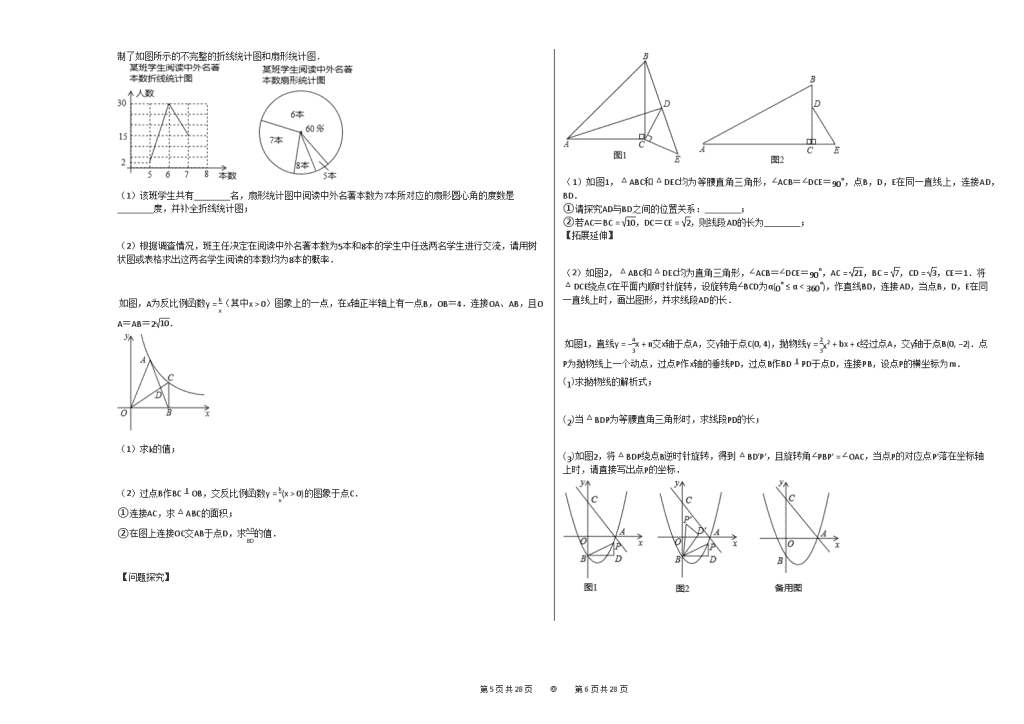
【问题探究】
(1)①由“SAS”可证△ACD≅△BCE,可得∠ADC=∠BEC=45∘,可得AD⊥BD;
②过点C作CF⊥AD于点F,由勾股定理可求DF,CF,AF的长,即可求AD的长;
【拓展延伸】
(2)分点D在BC左侧和BC右侧两种情况讨论,根据勾股定理和相似三角形的性质可求解.
【解答】
∵ △ABC和△DEC均为等腰直角三角形,
∴ AC=BC,CE=CD,∠ABC=∠DEC=45∘=∠CDE
∵ ∠ACB=∠DCE=90∘,
∴ ∠ACD=∠BCE,且AC=BC,CE=CD
∴ △ACD≅△BCE(SAS)
∴ ∠ADC=∠BEC=45∘
∴ ∠ADE=∠ADC+∠CDE=90∘
∴ AD⊥BD
故答案为:AD⊥BD
②如图,过点C作CF⊥AD于点F,
∵ ∠ADC=45∘,CF⊥AD,CD=2
∴ DF=CF=1
∴ AF=AC2−CF2=3
∴ AD=AF+DF=4
故答案为:4
【拓展延伸】
若点D在BC右侧,
如图,过点C作CF⊥AD于点F,
∵
第25页 共28页 ◎ 第26页 共28页
∠ACB=∠DCE=90∘,AC=21,BC=7,CD=3,CE=1.
∴ ∠ACD=∠BCE,ACBC=3=CDCE
∴ △ACD∽△BCE
∴ ∠ADC=∠BEC,
∵ CD=3,CE=1
∴ DE=DC2+CE2=2
∵ ∠ADC=∠BEC,∠DCE=∠CFD=90∘
∴ △DCE∽△CFD,
∴ DEDC=DCCF=CEDF
即23=3CF=1DF
∴ CF=32,DF=32
∴ AF=AC2−CF2=532
∴ AD=DF+AF=33
若点D在BC左侧,
∵ ∠ACB=∠DCE=90∘,AC=21,BC=7,CD=3,CE=1.
∴ ∠ACD=∠BCE,ACBC=3=CDCE
∴ △ACD∽△BCE
∴ ∠ADC=∠BEC,
∴ ∠CED=∠CDF
∵ CD=3,CE=1
∴ DE=DC2+CE2=2
∵ ∠CED=∠CDF,∠DCE=∠CFD=90∘
∴ △DCE∽△CFD,
∴ DEDC=DCCF=CEDF
即23=3CF=1DF
∴ CF=32,DF=32
∴ AF=AC2−CF2=532
∴ AD=AF−DF=23
【答案】
解:(1)∵ 点C(0, 4)在直线y=−43x+n上,
∴ n=4,
∴ y=−43x+4,
令y=0,
∴ x=3,
∴ A(3, 0).
∵ 抛物线y=23x2+bx+c经过点A,
交y轴于点B(0, −2).
∴ c=−2,
6+3b−2=0,
∴ b=−43,
∴ 抛物线解析式为y=23x2−43x−2;
(2)∵ 点P的横坐标为m,
∴ P(m, 23m2−43m−2),
当△BDP为等腰直角三角形时,PD=BD.
①当点P在直线BD上方时,
PD=23m2−43m,
若点P在y轴左侧,
则m<0,BD=−m,
∴ 23m2−43m=−m,
解得m1=0(舍去),m2=12(舍去);
若点P在y轴右侧,
则m>0,BD=m,
∴ 23m2−43m=m,
解得m1=0(舍去),m2=72.
②当点P在直线BD下方时,
m>0,BD=m,PD=−23m2+43m,
∴ −23m2+43m=m,
解得m1=0(舍去),m2=12.
综上所述,m=72或12.
即当△BDP
第25页 共28页 ◎ 第26页 共28页
为等腰直角三角形时,线段PD的长为72或12.
3∵ ∠PBP′=∠OAC,OA=3,OC=4,
∴ AC=5,
∴ sin∠PBP′=45,cos∠PBP′=35,
①当点P′落在x轴上时,过点D′作D′N⊥x轴,垂足为N,交BD于点M,
∠DBD′=∠ND′P′=∠PBP′,
如图1,
ND′−MD′=2,
∴ 35(23m2−43m)−(−45m)=2,
∴ m=5(舍),或m=−5,
如图2,
ND′+MD′=2,
∴ 35(23m2−43m)+45m=2,
∴ m=5,或m=−5(舍),
∴ P(−5, 45+43)或P(5, −45+43),
②当点P′落在y轴上时,如图3,
过点D′作D′M⊥x轴,交BD于M,过点P′作P′N⊥y轴,交MD′的延长线于点N,
∴ ∠DBD′=∠ND′P′=∠PBP′,
∵ P′N=BM,
∴ 45(23m2−43m)=35m,
∴ m=258,
∴ P(258, 1132).
∴ P(−5, 45+43)或P(5, −45+43)或P(258, 1132).
【考点】
二次函数综合题
【解析】
(1)先确定出点A的坐标,再用待定系数法求出抛物线解析式;
(2)由△BDP为等腰直角三角形,判断出BD=PD,建立m的方程计算出m,从而求出PD;
(3)分点P′落在x轴和y轴两种情况计算即可.
【解答】
解:(1)∵ 点C(0, 4)在直线y=−43x+n上,
∴ n=4,
∴ y=−43x+4,
令y=0,
∴ x=3,
∴ A(3, 0).
∵ 抛物线y=23x2+bx+c经过点A,
交y轴于点B(0, −2).
∴ c=−2,
6+3b−2=0,
∴ b=−43,
∴ 抛物线解析式为y=23x2−43x−2;
(2)∵ 点P的横坐标为m,
∴
第25页 共28页 ◎ 第26页 共28页
P(m, 23m2−43m−2),
当△BDP为等腰直角三角形时,PD=BD.
①当点P在直线BD上方时,
PD=23m2−43m,
若点P在y轴左侧,
则m<0,BD=−m,
∴ 23m2−43m=−m,
解得m1=0(舍去),m2=12(舍去);
若点P在y轴右侧,
则m>0,BD=m,
∴ 23m2−43m=m,
解得m1=0(舍去),m2=72.
②当点P在直线BD下方时,
m>0,BD=m,PD=−23m2+43m,
∴ −23m2+43m=m,
解得m1=0(舍去),m2=12.
综上所述,m=72或12.
即当△BDP为等腰直角三角形时,线段PD的长为72或12.
3∵ ∠PBP′=∠OAC,OA=3,OC=4,
∴ AC=5,
∴ sin∠PBP′=45,cos∠PBP′=35,
①当点P′落在x轴上时,过点D′作D′N⊥x轴,垂足为N,交BD于点M,
∠DBD′=∠ND′P′=∠PBP′,
如图1,
ND′−MD′=2,
∴ 35(23m2−43m)−(−45m)=2,
∴ m=5(舍),或m=−5,
如图2,
ND′+MD′=2,
∴ 35(23m2−43m)+45m=2,
∴ m=5,或m=−5(舍),
∴ P(−5, 45+43)或P(5, −45+43),
②当点P′落在y轴上时,如图3,
过点D′作D′M⊥x轴,交BD于M,过点P′作P′N⊥y轴,交MD′的延长线于点N,
∴ ∠DBD′=∠ND′P′=∠PBP′,
∵ P′N=BM,
∴ 45(23m2−43m)=35m,
∴ m=258,
∴ P(258, 1132).
∴ P(−5, 45+43)或P(5, −45+43)或P(258, 1132).
第25页 共28页 ◎ 第26页 共28页