- 2021-02-26 发布 |
- 37.5 KB |
- 34页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2015年数学理高考课件2-13 定积分与微积分基本定理
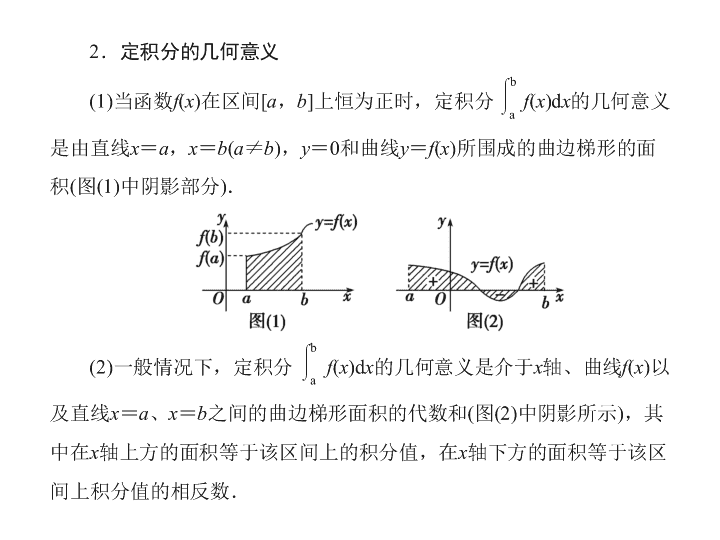
[ 最新考纲展示 ] 1 . 了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念. 2. 了解微积分基本定理的含义. 第十三节 定积分与微积分基本定理 定积分 答案: D 答案: D 微积分基本定理 F ( b ) - F ( a ) ____________________[ 通关方略 ]____________________ 利用微积分基本定理 ( 即牛顿 — 莱布尼兹公式 ) 求定积分,关键是找到满足 F ′ ( x ) = f ( x ) 的函数 F ( x ) ,即找被积函数 f ( x ) 的原函数 F ( x ) ,利用求导运算与求原函数运算互为逆运算的关系,运用基本初等函数求导公式和导数四则运算法则从反方向上求出 F ( x ) . 答案: C 答案: A 定积分计算 答案: e π - 1 反思总结 1 . 利用微积分基本定理求定积分,其关键是求出被积函数的原函数,求一个函数的原函数与求一个函数的导数是互逆运算,因此应注意掌握一些常见函数的导数. 2 .根据积分的几何意义可利用面积求积分. 利用定积分求平面图形的面积 [ 答案 ] D 反思总结 利用定积分求曲边梯形面积的步骤 (1) 画出曲线的草图. (2) 借助图形,确定被积函数,求出交点坐标,确定积分的上、下限. (3) 将 “ 曲边梯形 ” 的面积表示成若干个定积分的和或差. (4) 计算定积分,写出答案. 变式训练 2 .不等式 x 2 - 2 x <0 表示的平面区域与抛物线 y 2 = 4 x 围成的封闭区域的面积是 ________ . 定积分在物理中的应用 [ 解析 ] 由于 F ( x ) 与位移方向成 30° 角.如图: F 在位移方向上的分力 F ′ = F · cos 30° , [ 答案 ] C 变式训练 3 . (2014 年广州模拟 ) 物体 A 以 v = 3 t 3 + 1(m/s) 的速度在一直线 l 上运动,物体 B 在直线 l 上,且在物体 A 的正前方 5 m 处,同时以 v = 10 t (m/s) 的速度与 A 同向运动,出发后物体 A 追上物体 B 所用的时间 t (s) 为 ( ) A . 3 B . 4 C . 5 D . 6 答案: C —— 定积分的创新交汇问题 定积分的考查是各地高考命题的热点,近几年将定积分与概率、数列、二项式定理等知识交汇命题是高考题一大热点,归纳起来有如下几个角度: 定积分与概率计算交汇命题 由题悟道 作出可行域利用定积分计算出所需部分平面图形的面积,然后求出概率. 定积分与数列交汇命题 [ 答案 ] ln 101 由题悟道 利用定积分求出数列通项后,借助于数列裂项求和的方法可求和. 答案: A 2. 如图,圆 O : x 2 + y 2 = π 2 内的正弦曲线 y = sin x 与 x 轴围成的区域记为 M ( 图中阴影部分 ) ,随机往圆 O 内投一个点 A ,则点 A 落在区域 M 内的概率是 ________ . 本小节结束 请按 ESC 键返回查看更多