历届数学高考中的试题精选空间向量与立体几何

历届数学高考中的试题精选空间向量与立体几何

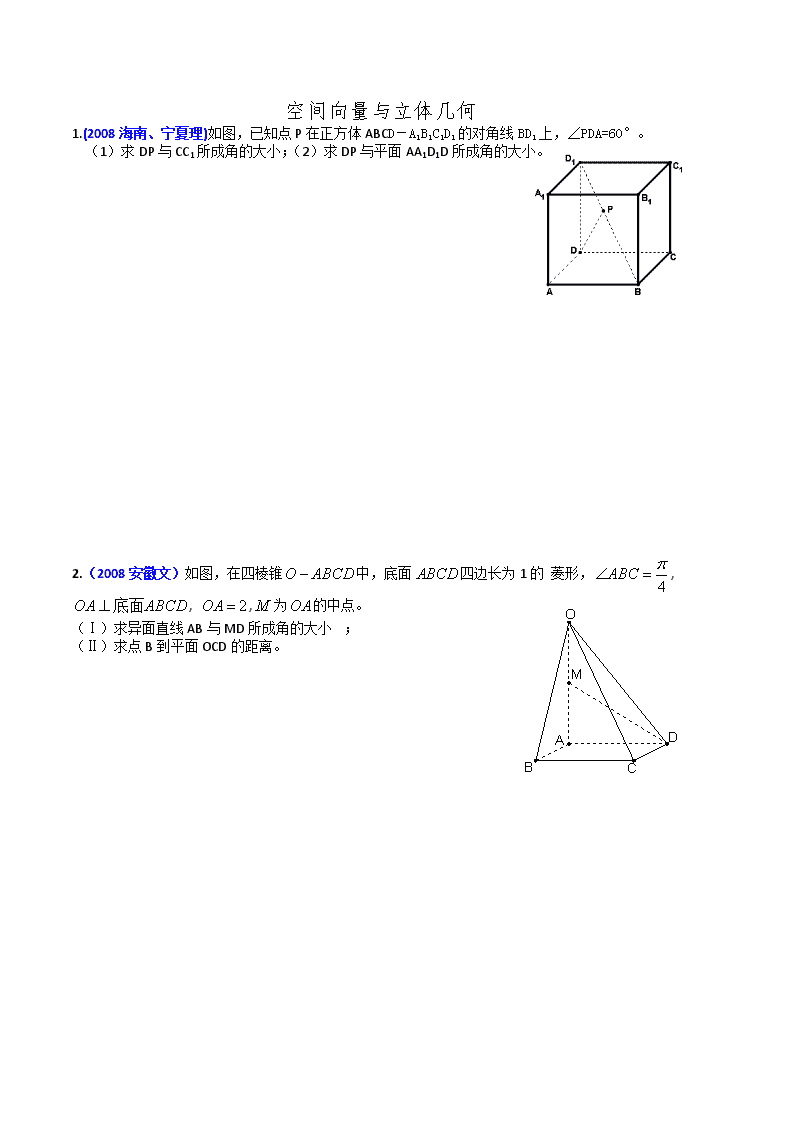
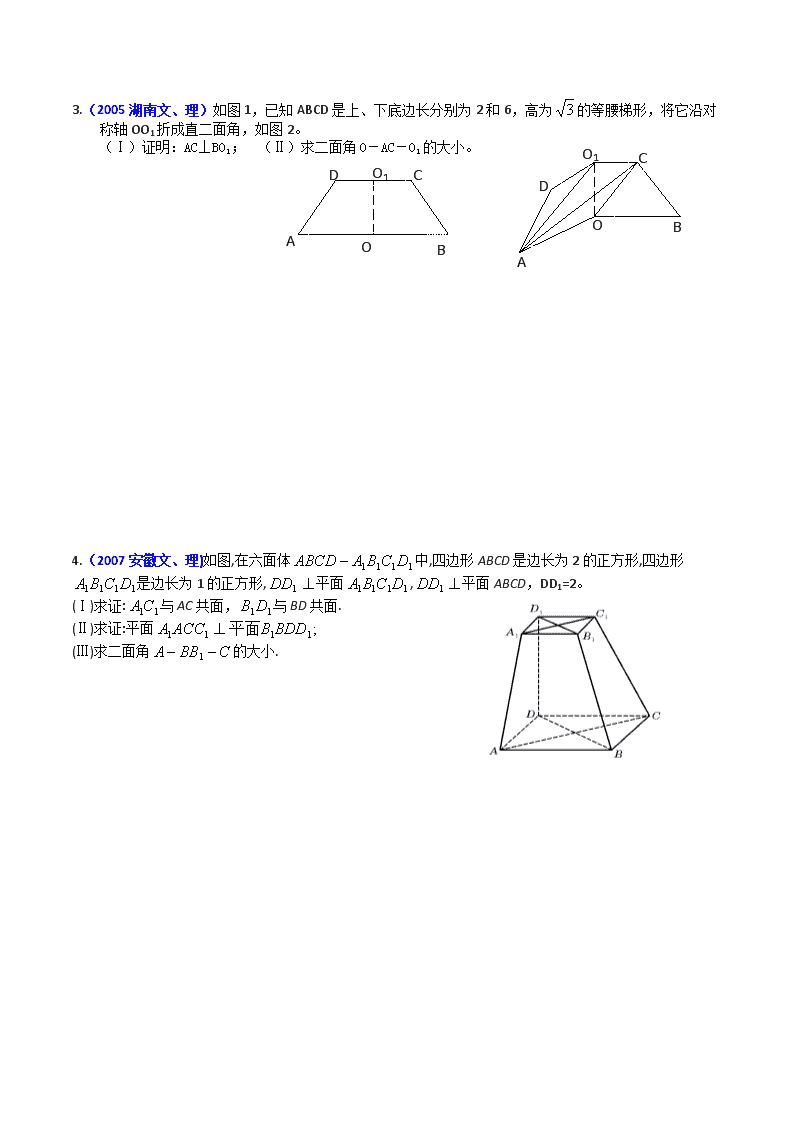
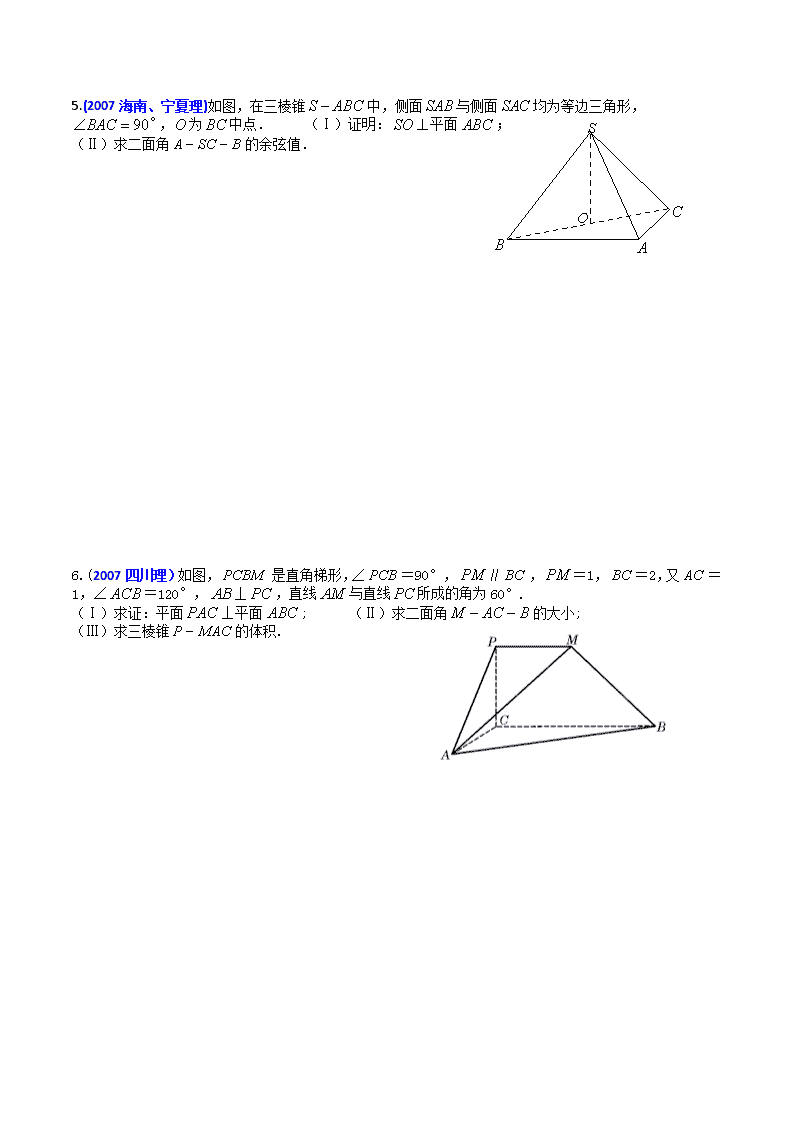
‎ 空间向量与立体几何 ‎ ‎1.(2008海南、宁夏理)如图，已知点P在正方体ABCD－A1B‎1C1D1的对角线BD1上，∠PDA=60°。‎ ‎（1）求DP与CC1所成角的大小；（2）求DP与平面AA1D1D所成角的大小。‎ ‎2.（2008安徽文）如图，在四棱锥中，底面四边长为1的 菱形，, , ,为的中点。‎ ‎（Ⅰ）求异面直线AB与MD所成角的大小；‎ ‎（Ⅱ）求点B到平面OCD的距离。‎ A B C D O O1‎ A B O C O1‎ D ‎3.（2005湖南文、理）如图1，已知ABCD是上、下底边长分别为2和6，高为的等腰梯形，将它沿对称轴OO1折成直二面角，如图2。‎ ‎　　（Ⅰ）证明：AC⊥BO1； （Ⅱ）求二面角O－AC－O1的大小。‎ ‎4.（2007安徽文、理)如图,在六面体中,四边形ABCD是边长为2的正方形,四边形是边长为1的正方形,平面,平面ABCD，DD1=2。‎ ‎(Ⅰ)求证:与AC共面，与BD共面. ‎ ‎(Ⅱ)求证:平面 ‎ ‎(Ⅲ)求二面角的大小.‎ ‎5.(2007海南、宁夏理)如图，在三棱锥中，侧面与侧面均为等边三角形，，为中点． （Ⅰ）证明：平面；‎ ‎（Ⅱ）求二面角的余弦值．‎ ‎6.(2007四川理）如图，是直角梯形，∠＝90°，∥，＝1，＝2，又＝1，∠＝120°，⊥，直线与直线所成的角为60°. ‎ ‎（Ⅰ）求证：平面⊥平面; （Ⅱ）求二面角的大小;‎ ‎（Ⅲ）求三棱锥的体积.‎ A B M N C l2‎ l1‎ H ‎7.(2006全国Ⅰ卷文、理)如图，、是互相垂直的异面直线,MN是它们的公垂线段.点A、B在上，C在上，。 （Ⅰ）证明AC⊥NB；‎ ‎(Ⅱ)若，求与平面ABC所成角的余弦值。‎ ‎8.（2006福建文、理）如图，四面体ABCD中，O、E分别是BD、BC的中点，‎ ‎（I）求证：平面BCD； （II）求异面直线AB与CD所成角的大小；‎ ‎（III）求点E到平面ACD的距离。‎ 历届高考中的“空间向量与立体几何”试题选讲(参考答案)‎ ‎1．解：如图，以为原点，为单位长建立空间直角坐标系．‎ 则，．连结，．‎ 在平面中，延长交于．设，‎ 由已知，由 A B C D P x y z H 可得．解得，所以．‎ ‎（Ⅰ）因为，‎ 所以．即与所成的角为．‎ ‎（Ⅱ）平面的一个法向量是．‎ 因为，‎ 所以．‎ 可得与平面所成的角为．‎ ‎2．解：作于点P,如图,分别以AB,AP,AO所在直线为轴建立坐标系,‎ ‎(1)设与所成的角为,‎ ‎ , ‎ 与所成角的大小为 ‎(2) ‎ 设平面OCD的法向量为,则 即 取,解得 设点B到平面OCD的距离为,则为在向量上的投影的绝对值,‎ ‎ , .‎ 所以点B到平面OCD的距离为 ‎3．解:（I）证明 由题设知OA⊥OO1，OB⊥OO1. ‎ ‎ 所以∠AOB是所折成的直二面角的平面角，‎ ‎ 即OA⊥OB. 故可以O为原点，OA、OB、OO1‎ ‎ 所在直线分别为轴、y轴、z轴建立空间直角坐标系，‎ ‎ 如图3，则相关各点的坐标是A（3，0，0），‎ ‎ B（0，3，0），C（0，1，）,O1（0，0，）. ‎ 从而，‎ ‎ 所以AC⊥BO1. ‎ ‎（II）解：因为所以BO1⊥OC，‎ 由（I）AC⊥BO1，所以BO1⊥平面OAC，是平面OAC的一个法向量.‎ 设是0平面O‎1AC的一个法向量，‎ 由 得. ‎ 设二面角O—AC—O1的大小为，由、的方向可知，>，‎ ‎ 所以cos，>=‎ ‎4.解（向量法）：以D为原点，以DA,DC,所在直线分别为x轴，y轴，z轴建立空间直角坐标系如图，则有A（2，0，0），B（2，2，0），C（0，2，0），‎ ‎（Ⅰ）证明：‎ 于是与AC共面，与BD共面.‎ ‎（Ⅱ）证明：‎ 内的两条相交直线，‎ ‎ 又平面 ‎（Ⅲ）解：‎ 设 于是 设 于是 ‎5．证明：（Ⅰ）由题设，连结，‎ 为等腰直角三角形，所以，且，‎ 又为等腰三角形，故，且，‎ 从而．所以为直角三角形，．‎ 又．‎ 所以平面．‎ ‎（Ⅱ）解：以为坐标原点，射线分别为轴、轴的正半轴，建立如图的空间直角坐标系．设，则．‎ 的中点，．‎ ‎．‎ 故等于二面角的平面角．‎ ‎，‎ 所以二面角的余弦值为．‎ ‎6．解： （Ⅰ）∵‎ ‎∴，‎ 又∵‎ ‎∴‎ ‎（Ⅱ）在平面内，过作，建立空间直角坐标系（如图）‎ 由题意有，设，‎ 则 由直线与直线所成的解为，得 ‎，即，‎ 解得 ‎∴，设平面的一个法向量为，‎ 则，取，得 平面的法向量取为 设与所成的角为，则 显然，二面角的平面角为锐角，‎ 故二面角的平面角大小为 ‎（Ⅲ）解法一：由（Ⅱ）知，为正方形 ‎∴‎ ‎（Ⅲ）解法二：取平面的法向量取为，则点A到平面的距离 ‎∵，‎ ‎∴‎ ‎7．解: 如图,建立空间直角坐标系M－xyz.令MN=1, ‎ 则有A(－1,0,0),B(1,0,0),N(0,1,0),‎ ‎(Ⅰ)∵MN是 l1、l2的公垂线, l1⊥l2, ∴l2⊥平面ABN. l2平行于z轴. ‎ 故可设C(0,1,m).于是 =(1,1,m), =(1,－1,0). ‎ ‎∴·=1+(－1)+0=0 ∴AC⊥NB.‎ A B M N C l2‎ l1‎ H x y z ‎(Ⅱ)∵ =(1,1,m), =(－1,1,m), ∴||=||, 又已知∠ACB=60°,∴△ABC为正三角形,AC=BC=AB=2. 在Rt△CNB中,NB=, 可得NC=,故C(0,1, ).‎ 连结MC,作NH⊥MC于H,设H(0,λ, λ) (λ>0). ‎ ‎∴=(0,1－λ,－λ), ‎ =(0,1, ). · = 1－λ－2λ=0, ∴λ= ,‎ ‎∴H(0, , ), 可得=(0,, － ), 连结BH,则=(－1,, ),‎ ‎∵·=0+ － =0, ∴⊥, 又MC∩BH=H,∴HN⊥平面ABC,‎ ‎∠NBH为NB与平面ABC所成的角.又=(－1,1,0),‎ ‎∴cos∠NBH= = = ‎8． (1)证明：连结OC. ∵BO=DO,AB=AD, ∴AO⊥BD. ∵BO=DO,BC=CD, ∴CO⊥BD. 在△AOC中，由已知可得AO=1,CO=.而AC=2,‎ ‎∴AO2+CO2=AC2, ∴∠AOC=90°,即AO⊥OC.‎ ‎∴AO平面BCD.‎ ‎（Ⅱ）解：以O为原点，如图建立空间直角坐标系，则B(1，0，0)，D(-1，0，0)，‎ C(0，，0)，A(0,0,1),E(,,0),‎ ‎ ‎ ‎∴‎ ‎∴异面直线AB与CD所成角的大小为 ‎（Ⅲ）解法一：设平面ACD的法向量为n=(x,y,z),则 ‎ ‎ ∴‎ 令y=1，得n=(-)是平面ACD的一个法向量.又 ‎∴点E到平面ACD的距离h=‎ ‎（Ⅲ）解法二：设点E到平面ACD的距离为h.‎ ‎,‎ ‎∴·S△ACD =·AO·S△CDE.‎ 在△ACD中，CA=CD=2,AD=,‎ ‎∴S△ACD=而AO=1, S△CDE=‎ ‎∴h=‎ ‎∴点E到平面ACD的距离为.‎ w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com