- 2021-05-10 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级数学上册第二十二章二次函数22-1二次函数的图象和性质3y=ax2+k(a≠0)教学课件新版 人教版
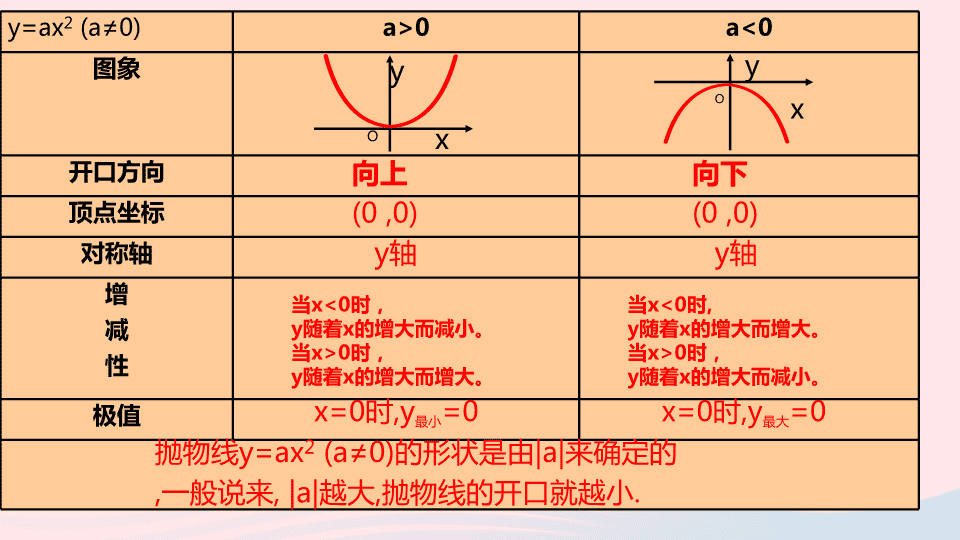
第 22 章:二次函数 22.1 二次函数的图像和性质 22.1.3 y=ax²+k (a≠0) 学习目标: 1.会用描点法画出二次函数y=ax²+k (a≠0)的图象,并通过图象归纳其性质。 2.了解抛物线y=ax² (a≠0) 与y=ax²+k (a≠0) 之间的位置关系。 3.灵活运用二次函数y=ax²+k (a≠0) 的图象及性质解决有关问题。 y=ax 2 (a≠0) a>0 a<0 图象 开口方向 顶点坐标 对称轴 增 减 性 极值 x y O y x O 向上 向下 (0 ,0) (0 ,0) y 轴 y 轴 当 x<0 时, y 随着 x 的增大而减小。 当 x>0 时, y 随着 x 的增大而增大。 当 x<0 时 , y 随着 x 的增大而增大。 当 x>0 时, y 随着 x 的增大而减小。 x=0 时 ,y 最小 =0 x=0 时 ,y 最大 =0 抛物线 y=ax 2 (a≠0) 的形状是由 |a| 来确定的 , 一般说来 , |a| 越大 , 抛物线的开口就越小 . x ….. -2 -1 0 1 2 …… y=x 2 …… 4 1 0 1 4 y=x 2 +1 …… …… y=x 2 y=x 2 +1 5 2 1 2 5 函数 y=x 2 +1 的图象与 y=x 2 的图象的位置有什么关系 ? 函数 y=x 2 +1 的图象可由 y=x 2 的图象沿 y 轴向 上 平移 1 个单位长度得到 . 函数 y=x 2 +1 的图象与 y=x 2 的图象的形状相同吗 ? 相同 x ….. -2 -1 0 1 2 …… y=x 2 …… 4 1 0 1 4 y=x 2 -2 …… …… y=x 2 y=x 2 -2 2 -1 -2 -1 2 函数 y=x 2 -2 的图象可由 y=x 2 的图象沿 y 轴向 下 平移 2 个单位长度得到 . 函数 y=x 2 -2 的图象与 y=x 2 的图象的位置有什么关系 ? 函数 y=x 2 +1 的图象与 y=x 2 的图象的形状相同吗 ? 相同 函数 y=ax 2 (a≠0) 和函数 y=ax 2 +k (a≠0) 的图象形状 ,只是位置不同;当 k>0 时,函数 y=ax 2 +k 的图象可由 y=ax 2 的图象向 平移 个单位得到,当 k〈0 时,函数 y=ax 2 +k 的图象可由 y=ax 2 的图象 向 平移 个单位得到。 y=-x 2 -2 y=-x 2 +3 y=-x 2 函数 y=-x 2 -2 的图象可由 y=-x 2 的图象沿 y 轴向 下 平移 2 个单位长度得到 . 函数 y=-x 2 +3 的图象可由 y=-x 2 的图象沿 y 轴向 上 平移 3 个单位长度得到 . 图象向上移还是向下移 , 移多少个单位长度 , 有什么规律吗 ? 上加下减 相同 上 k 下 |k| (1) 函数 y=4x 2 +5 的图象可由 y=4x 2 的图象 向 平移 个单位得到; y=4x 2 -11 的图象 可由 y=4x 2 的图象向 平移 个单位得到。 (2) 将函数 y=-3x 2 +4 的图象向 平移 个单位可得 y=-3x 2 的图象;将 y=2x 2 -7 的图象向 平移 个 单位得到 y=2x 2 的图象。将 y=x 2 -7 的图象 向 平移 个单位可得到 y=x 2 +2 的图象。 上 5 下 11 下 4 上 7 上 9 ( 3 )将抛物线 y=4x 2 向上平移 3 个单位, 所得的抛物线的函数式是 。 将抛物线 y=-5x 2 +1 向下平移 5 个单位 , 所得的抛物线的函数式是 。 y=4x 2 +3 y=-5x 2 -4 y=x 2 -2 y=x 2 +1 y=x 2 y=-x 2 -2 y=-x 2 +3 y=-x 2 当 a>0 时,抛物线 y=ax 2 +c 的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧, y 随 x 的增大而 ,在对称轴的右侧 ,y 随 x 的增大而 , 当 x= 时,取得最 值,这个值等于 ; 当 a<0 时 , 抛物线 y=ax 2 +c 的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧, y 随 x 的增大而 ,在对称轴的右侧 ,y 随 x 的增大而 ,当 x= 时,取得最 值,这个值等于 。 向上 y 轴 (0,c) 减小 增大 0 小 c 向下 y 轴 (0,c) 增大 减小 0 大 c ( 4 )抛物线 y=-3x 2 +5 的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧, y 随 x 的增大而 ,在对称轴的右侧, y 随 x 的增大而 , 当 x= 时,取得最 值,这个值等于 。 ( 5 )抛物线 y=7x 2 -3 的开口 ,对称轴是 ,顶点坐标是 ,在对称轴的左侧, y 随 x 的增大而 ,在对称轴的右侧, y 随 x 的增大而 , 当 x= 时,取得最 值,这个值等于 。 下 y 轴 (0,5) 减小 增大 0 大 5 上 y 轴 (0,-3) 减小 增大 0 小 -3 6. 二次函数 y=ax 2 +c (a≠0) 的图象经过点 A ( 1 , -1 ), B ( 2 , 5 ),则函数 y=ax 2 +c 的表达式为 。若点 C(-2,m),D ( n ,7 )也在函数的图象上,则点 C 的坐标为 点 D 的坐标为 . y=2x 2 -3 (-2,5) 或 y=ax 2 +k (a≠0) a>0 a<0 开口方向 顶点坐标 对称轴 增 减 性 极值 向上 向下 (0 ,k) (0 ,k) y 轴 y 轴 当 x<0 时, y 随着 x 的增大而减小。 当 x>0 时, y 随着 x 的增大而增大。 当 x<0 时 , y 随着 x 的增大而增大。 当 x>0 时, y 随着 x 的增大而减小。 x=0 时 ,y 最小 =k x=0 时 ,y 最大 =k 抛物线 y=ax 2 +k (a≠0) 的图象可由 y=ax 2 的图象通过上下平移得到 . (1) 已知二次函数 y=3x 2 +4, 点 A(x 1 ,y 1 ), B(x 2 ,y 2 ), C(x 3 ,y 3 ), D(x 4 ,y 4 ) 在其图象上 , 且 x 2 < x 4 <0, 0查看更多