- 2021-05-08 发布 |
- 37.5 KB |
- 5页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学之四边形周长最小值
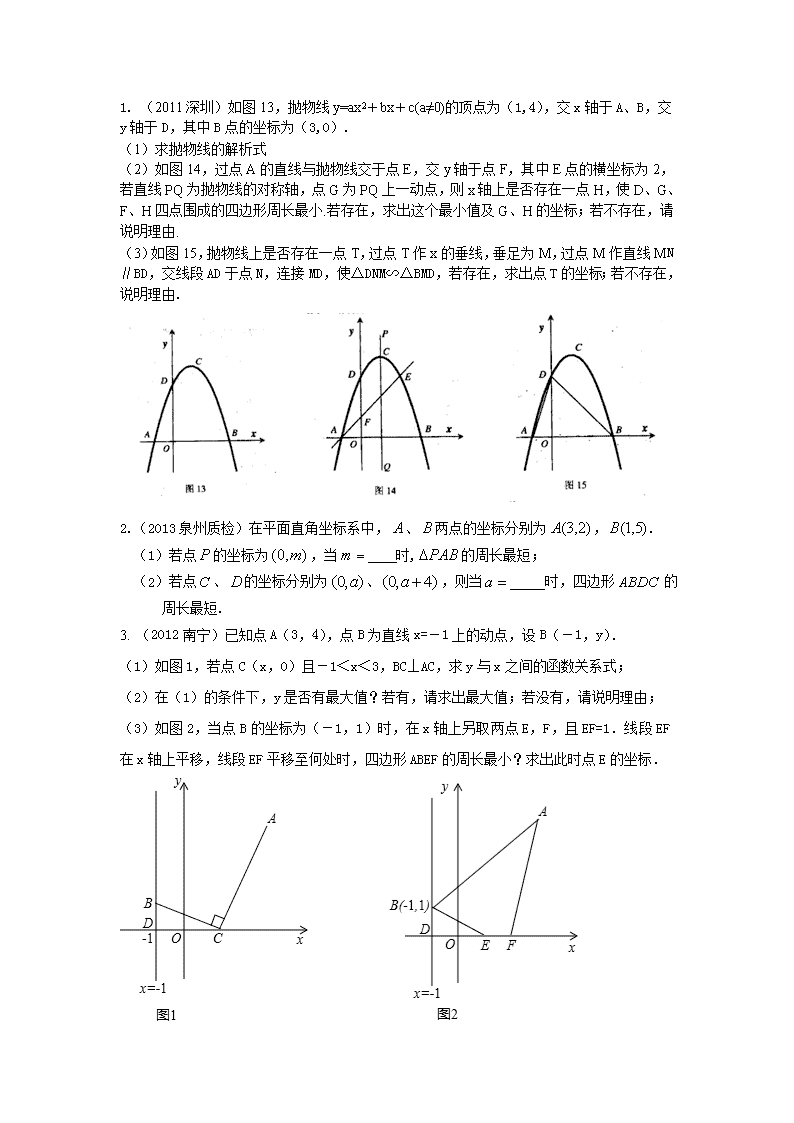
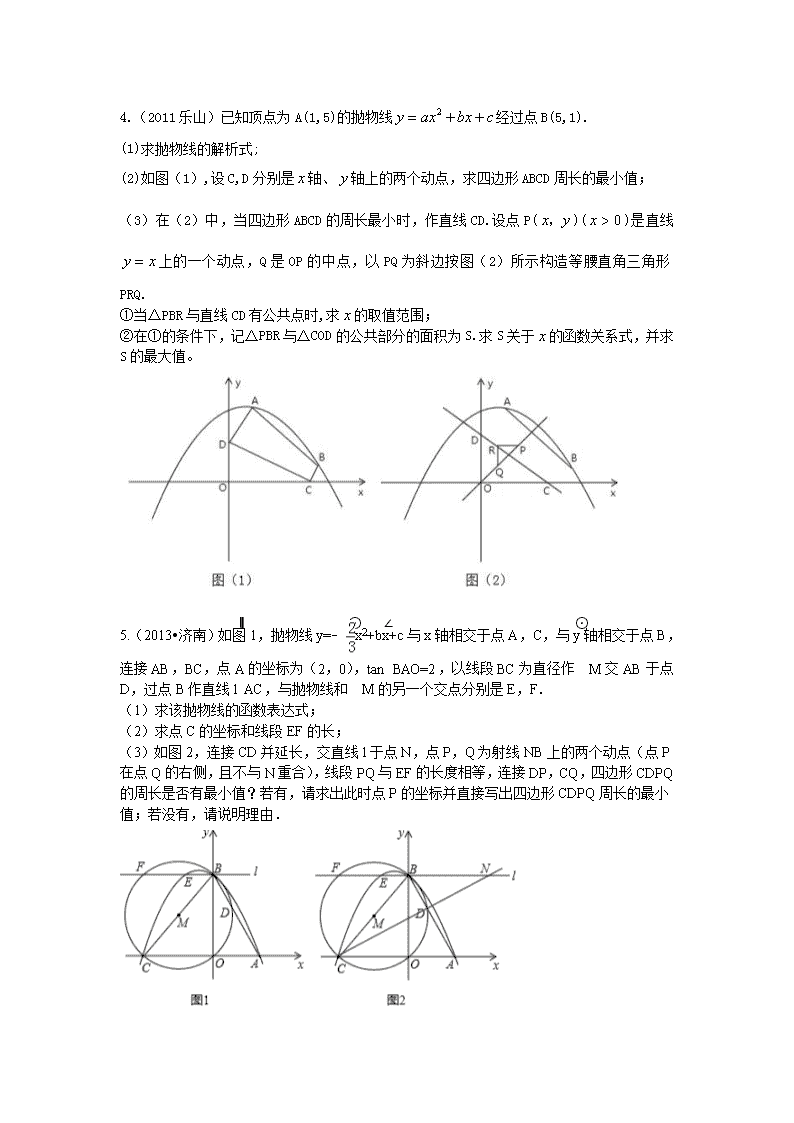
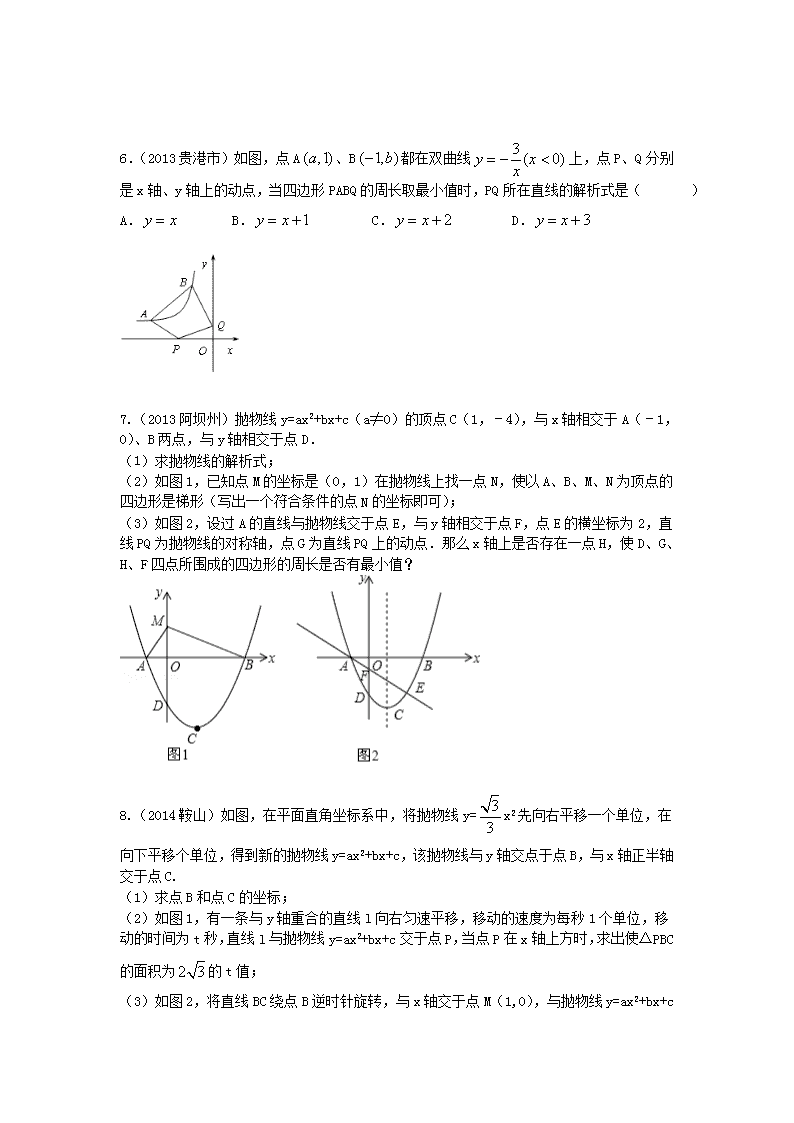
1. (2011深圳)如图13,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0). (1)求抛物线的解析式 (2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由. (3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由. 2.(2013泉州质检)在平面直角坐标系中,、两点的坐标分别为,. (1)若点的坐标为,当 时,的周长最短; (2)若点、的坐标分别为、,则当 时,四边形的周长最短. 3. (2012南宁)已知点A(3,4),点B为直线x=-1上的动点,设B(-1,y). (1)如图1,若点C(x,0)且-1<x<3,BC⊥AC,求y与x之间的函数关系式; (2)在(1)的条件下,y是否有最大值?若有,请求出最大值;若没有,请说明理由; (3)如图2,当点B的坐标为(-1,1)时,在x轴上另取两点E,F,且EF=1.线段EF在x轴上平移,线段EF平移至何处时,四边形ABEF的周长最小?求出此时点E的坐标. 4.(2011乐山)已知顶点为A(1,5)的抛物线经过点B(5,1). (1)求抛物线的解析式; (2)如图(1),设C,D分别是轴、轴上的两个动点,求四边形ABCD周长的最小值; (3)在(2)中,当四边形ABCD的周长最小时,作直线CD.设点P()()是直线上的一个动点,Q是OP的中点,以PQ为斜边按图(2)所示构造等腰直角三角形PRQ. ①当△PBR与直线CD有公共点时,求的取值范围; ②在①的条件下,记△PBR与△COD的公共部分的面积为S.求S关于的函数关系式,并求S的最大值。 5.(2013•济南)如图1,抛物线y=﹣x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F. (1)求该抛物线的函数表达式; (2)求点C的坐标和线段EF的长; (3)如图2,连接CD并延长,交直线l于点N,点P,Q为射线NB上的两个动点(点P在点Q的右侧,且不与N重合),线段PQ与EF的长度相等,连接DP,CQ,四边形CDPQ的周长是否有最小值?若有,请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值;若没有,请说明理由. 6.(2013贵港市)如图,点A、B都在双曲线上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( ) A. B. C. D. 7.(2013阿坝州)抛物线y=ax2+bx+c(a≠0)的顶点C(1,﹣4),与x轴相交于A(﹣1,0)、B两点,与y轴相交于点D. (1)求抛物线的解析式; (2)如图1,已知点M的坐标是(0,1)在抛物线上找一点N,使以A、B、M、N为顶点的四边形是梯形(写出一个符合条件的点N的坐标即可); (3)如图2,设过A的直线与抛物线交于点E,与y轴相交于点F,点E的横坐标为2,直线PQ为抛物线的对称轴,点G为直线PQ上的动点.那么x轴上是否存在一点H,使D、G、H、F四点所围成的四边形的周长是否有最小值? 8.(2014鞍山)如图,在平面直角坐标系中,将抛物线y=x2先向右平移一个单位,在向下平移个单位,得到新的抛物线y=ax2+bx+c,该抛物线与y轴交点于点B,与x轴正半轴交于点C. (1)求点B和点C的坐标; (2)如图1,有一条与y轴重合的直线l向右匀速平移,移动的速度为每秒1个单位,移动的时间为t秒,直线l与抛物线y=ax2+bx+c交于点P,当点P在x轴上方时,求出使△PBC的面积为的t值; (3)如图2,将直线BC绕点B逆时针旋转,与x轴交于点M(1,0),与抛物线y=ax2+bx+c 交于点A,在y轴上有一点D(0,),在x轴上另取两点E、F(点E在点F的左侧)EF=2,线段EF在x轴上平移,当四边形ADEF的周长最小时,先简单描述如何确定此时点E的位置?在直接写出点E的坐标。 9.(2014•海南)如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点. (1)求此抛物线的解析式; (2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标; (3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由. 10.(2014广州)已知平面直角坐标系中两定点、,抛物线过点顶点为,点为抛物线上一点. (1)求抛物线的解析式和顶点的坐标; (2)当为钝角时,求的取值范围; (3)若当为直角时,将该抛物线向左或向右平移个单位,点、平移后对应的点分别记为,是否存在,使得首尾依次连接所构成的多边形的周长最短?若存在,求的值并说明抛物线平移的方向;若不存在,请说明理由. 11.(2014•乌鲁木齐)在平面直角坐标系xOy中,抛物线y=mx2﹣2x与x轴正半轴交于点A,顶点为B. (1)求点B的坐标(用含m的代数式表示); (2)已知点C(0,﹣2),直线AC与BO相交于点D,与该抛物线对称轴交于点E,且△OCD≌△BED,求m的值; (3)在由(2)确定的抛物线上有一点N(n,﹣),N在对称轴的左侧,点F,G在对称轴上,F在G上方,且FG=1,当四边形ONGF的周长最小时: ①求点F的坐标; ②设点P在抛物线上,在y轴上是否存在点H,使以N,F,H,P为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.查看更多