2015年高考数学(文科)真题分类汇编E单元 不等式
数 学
E 单元 不等式
E1 不等式的概念与性质
12.A2、E1[2015·福建卷] “对任意 x∈0,π
2
,ksin xcos x
0.故选项 A
中的不是最低费用;(ay+bz+cx)-(az+by+cx)=a(y-z)+b(z-y)=(a-b)(y-z)>0,故选项
C 中的不是最低费用;(ay+bx+cz)-(az+by+cx)=a(y-z)+b(x-y)+c(z-x)=a(y-z)+b(x
-y)+c(z-y+y-x)=(a-c)(y-z)+(b-c)(x-y)>0,选项 D 中的不是最低费用.
综上所述,选项 B 中的为最低费用.
E2 绝对值不等式的解法
21.E2,B3,B12[2015·广东卷] 设 a 为实数,函数 f(x)=(x-a)2+|x-a|-a(a-1).
(1)若 f(0)≤1,求 a 的取值范围;
(2)讨论 f(x)的单调性;
(3)当 a≥2 时,讨论 f(x)+4
x
在区间(0,+∞)内的零点个数.
4.A2、E2[2015·天津卷] 设 x∈R,则“10,
解得2
30,故 g(x)为增函数;
当-10 时,g′(x)>0,故 g(x)为增函数.
综上知 g(x)在(-∞,-4)和(-1,0)上为减函数,在(-4,-1)和(0,+∞)上为增函数.
11.E3[2015·广东卷] 不等式-x2-3x+4>0 的解集为________.(用区间表示)
11.(-4,1) [解析] 由-x2-3x+4>0 得-40 的解集
为(-4,1).
E4 简单的一元高次不等式的解法
E5 简单的线性规划问题
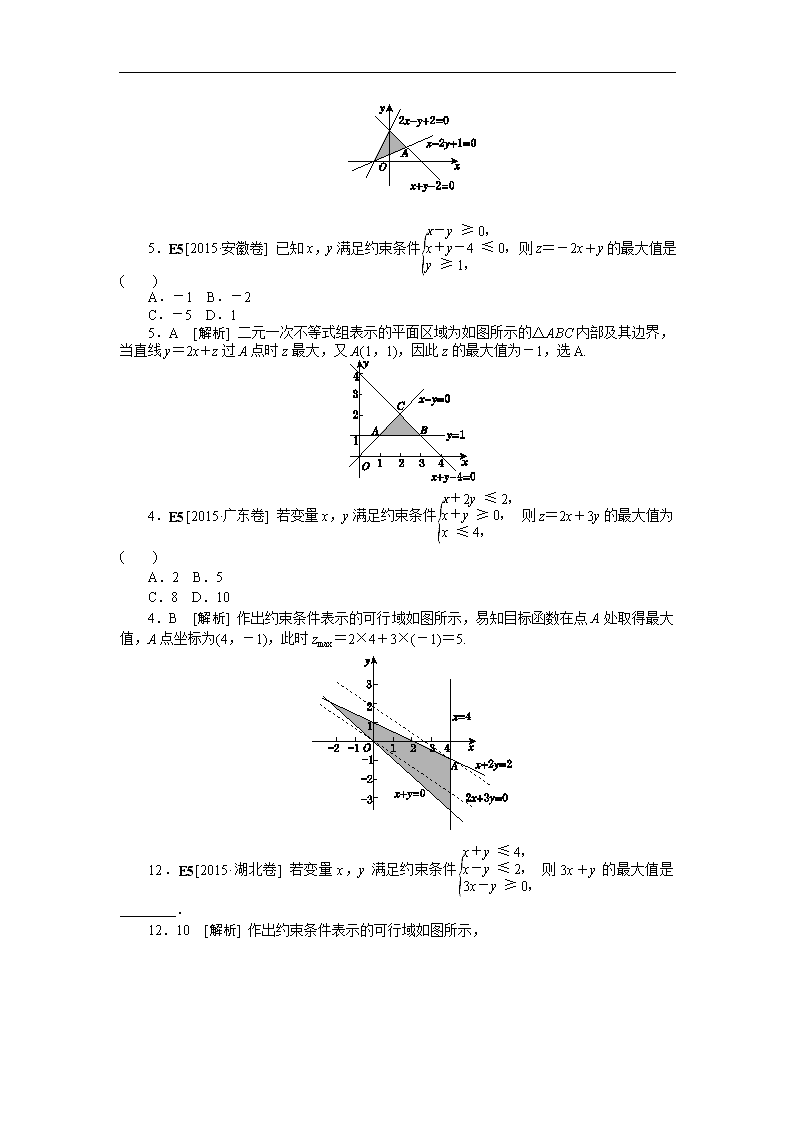
15.E5[2015·全国卷Ⅰ] 若 x,y 满足约束条件
x+y-2≤0,
x-2y+1≤0,
2x-y+2≥0,
则 z=3x+y 的最大值为
________.
15.4 [解析] 作出约束条件表示的可行域如图所示,当目标函数线平移至经过可行域
的顶点 A(1,1)时,目标函数 z 取得最大值,故 zmax=3×1+1=4.
5.E5[2015·安徽卷] 已知 x,y 满足约束条件
x-y≥0,
x+y-4≤0,
y≥1,
则 z=-2x+y 的最大值是
( )
A.-1 B.-2
C.-5 D.1
5.A [解析] 二元一次不等式组表示的平面区域为如图所示的△ABC 内部及其边界,
当直线 y=2x+z 过 A 点时 z 最大,又 A(1,1),因此 z 的最大值为-1,选 A.
4.E5[2015·广东卷] 若变量 x,y 满足约束条件
x+2y≤2,
x+y≥0,
x≤4,
则 z=2x+3y 的最大值为
( )
A.2 B.5
C.8 D.10
4.B [解析] 作出约束条件表示的可行域如图所示,易知目标函数在点 A 处取得最大
值,A 点坐标为(4,-1),此时 zmax=2×4+3×(-1)=5.
12.E5[2015·湖北卷] 若变量 x,y 满足约束条件
x+y≤4,
x-y≤2,
3x-y≥0,
则 3x+y 的最大值是
________.
12.10 [解析] 作出约束条件表示的可行域如图所示,
易知可行域边界三角形的三个顶点坐标分别是(3,1),(1,3),(-1,-3).将三个顶点
的坐标依次代入 3x+y,求得的值分别为 10,6,-6,比较可得 3x+y 的最大值为 10.
15.E5[2015·全国卷Ⅰ] 若 x,y 满足约束条件
x+y-2≤0,
x-2y+1≤0,
2x-y+2≥0,
则 z=3x+y 的最大值为
________.
15.4 [解析] 作出约束条件表示的可行域如图所示,当目标函数线平移至经过可行域
的顶点 A(1,1)时,目标函数 z 取得最大值,故 zmax=3×1+1=4.
14.E5[2015·全国卷Ⅱ] 若 x,y 满足约束条件
x+y-5≤0,
2x-y-1≥0,
x-2y+1≤0,
则 z=2x+y 的最大值为
________.
14.8 [解析] 根据约束条件作出可行域如图所示,平移目标函数线,当它经过点 A(3,
2)时,目标函数取得最大值,zmax=2×3+2=8.
13.E5[2015·北京卷] 如图 13,△ABC 及其内部的点组成的集合记为 D,P(x,y)为 D
中任意一点,则 z=2x+3y 的最大值为________.
图 13
13.7 [解析] 根据题意,z=2x+3y 变形为 y=-2
3x+1
3z,直线 AC 的斜率为 k=2-1
0-2
=
-1
2>-2
3
,利用求目标函数最值的方法,当 y=-2
3x+1
3z 过点 A(2,1)时 z 取得最大值 zmax=
2×2+3×1=7.
10.E5[2015·福建卷] 变量 x,y 满足约束条件
x+y≥0,
x-2y+2≥0,
mx-y≤0.
若 z=2x-y 的最大值为 2,
则实数 m 等于( )
A.-2 B.-1 C.1 D.2
10.C [解析] 由约束条件可知,
①若 m∈[2,+∞),则当 x=0,
y=0
时, zmax=0(舍去);
②若 m∈1
2
,2,则当 x-2y+2=0,
mx-y=0,
即
x= 2
2m-1
,
y= 2m
2m-1
时, zmax=2× 2
2m-1
- 2m
2m-1
=2,
所以 m=1;
③若 m∈-∞,1
2
,则 z 无最大值(舍去).
4.E5[2015·湖南卷] 若变量 x,y 满足约束条件
x+y≥1,
y-x≤1,
x≤1,
则 z=2x-y 的最小值为( )
A.-1 B.0
C.1 D.2
4.A [解析] 画出可行域如图中阴影部分所示,平移直线 2x-y=0,可知在直线 x+y
=1 与 y-x=1 的交点 A(0,1)处 z 取最小值,zmin=0-1=-1,选 A.
12.E5[2015·山东卷] 若 x,y 满足约束条件
y-x≤1,
x+y≤3,
y≥1,
则 z=x+3y 的最大值为________.
12.7 [解析] 作出可行域如图所示,当直线 x+3y-z=0 过可行域内的点 A 时,z 取
得最大值.联立 y-x=1,
x+y=3,
解得 x=1,
y=2,
即 A(1,2),故 zmax=1+3×2=7.
11.E5[2015·陕西卷] 某企业生产甲、乙两种产品均需用 A,B 两种原料.已知生产 1
吨每种产品所需原料及每天原料的可用限额如表所示.如果生产 1 吨甲、乙产品可获利润分
别为 3 万元、4 万元,则该企业每天可获得最大利润为( )
甲 乙 原料限额
A(吨) 3 2 12
B(吨) 1 2 8
A.12 万元 B.16 万元
C.17 万元 D.18 万元
11.D [解析] 设该企业每天生产甲种产品 x 吨、乙种产品 y 吨,则 x,y 需满足约束
条件
3x+2y≤12,
x+2y≤8,
x≥0,
y≥0,
可获利润 z=3x+4y.约束条件表示的平面区域是以(0,0),(4,0),(2,
3),(0,4)为顶点的四边形及其内部,把各顶点坐标代入检验可知,目标函数在点(2,3)处
取得最大值 3×2+4×3=18,即该企业每天可获得最大利润为 18 万元.
2.E5[2015·天津卷] 设变量 x,y 满足约束条件
x-2≤0,
x-2y≤0,
x+2y-8≤0,
则目标函数 z=3x+y 的
最大值为( )
A.7 B.8
C.9 D.14
2.C [解析] 已知不等式组表示的平面区域如图中的阴影部分所示,根据目标函数的
几何意义可知,目标函数在点 A(2,3)处取得最大值,且 zmax=9.
14.H4,E5[2015·浙江卷] 已知实数 x,y 满足 x2+y2≤1,则|2x+y-4|+|6-x-3y|的
最大值是________.
14.15 [解析] 方法一:当 x,y 满足 x2+y2≤1 时,2x+y-4<0,6-x-3y>0,
设 z=|2x+y-4|+|6-x-3y|,则 z=-2x-y+4+6-x-3y=-3x-4y+10,即 3x+4y
+z-10=0.由题意可知,|z-10|
5
≤1,即|z-10|≤5,所以 5≤z≤15,故所求最大值为 15.
方法二:坐标原点到直线 2x+y-4=0 和 6-x-3y=0 的距离分别是 4
5
,6
10
,均大于 1,
在 x,y 满足 x2+y2≤1 的条件下,2x+y-4≤0,6-x-3y≥0 恒成立.故在 x2+y2≤1 下,
|2x+y-4|+|6-x-3y|=-(2x+y-4)+(6-x-3y)=-3x-4y+10,令 m=-3x-4y,
则 y=-3
4x-m
4
,m 的几何意义是直线 m=-3x-4y 在 y 轴上的截距的-4 倍,若 m 最大,
则需要直线 m=-3x-4y 在 y 轴上的截距最小.
故只有当直线 m=-3x-4y 与单位圆 x2+y2=1 相切于第三象限时,m 取得最大值.此
时可求得切点坐标为-3
5
,-4
5
,故 mmax=-3× -3
5 -4× -4
5 =5,所以|2x+y-4|+|6-x
-3y|=-3x-4y+10 的最大值为 15.
10.E5[2015·重庆卷] 若不等式组
x+y-2≤0,
x+2y-2≥0,
x-y+2m≥0
表示的平面区域为三角形,且其面积
等于4
3
,则 m 的值为( )
A.-3 B.1
C.4
3 D.3
10.B [解析] 作出不等式组满足的平面区域,如图中阴影部分所示.由图可知,要使
不等式组表示的平面区域为三角形,则有 m>-1.由 x+y-2=0,
x-y+2m=0,
解得 x=1-m,
y=1+m,
即 A(1
-m,1+m).由 x+2y-2=0,
x-y+2m=0,
解得
x=2
3
-4
3m,
y=2
3
+2
3m,
即 B2
3
-4
3m,2
3
+2
3m.因为 S△ABC=S△ADC-S
△BDC=1
2(2+2m)(1+m)-2
3
+2m
3
=1
3(m+1)2=4
3
,解得 m=1 或 m=-3(舍去).故选 B.
E6 基本不等式
2
a bab
5.E6[2015·福建卷] 若直线x
a
+y
b
=1(a>0,b>0)过点(1,1),则 a+b 的最小值等于( )
A.2 B.3 C.4 D.5
5.C [解析] 依题意有1
a
+1
b
=1,所以 a+b=(a+b)·1
a
+1
b
=1+a
b
+b
a
+1≥2+2 a
b
·b
a
=4,当且仅当 a=b=2 时等号成立.
7.E6[2015·湖南卷] 若实数 a,b 满足1
a
+2
b
= ab,则 ab 的最小值为( )
A. 2 B.2
C.2 2 D.4
7.C [解析] 方法一:由已知得1
a
+2
b
=b+2a
ab
= ab,ab ab=b+2a≥2 2 ab,当且仅
当 b=2a=2 5
4
时,等号成立,所以 ab≥2 2.
方法二: ab=1
a
+2
b
≥2 2
ab
,即 ab≥2 2,当且仅当 b=2a=2 5
4
时,等号成立,选 C.
10.B7、E6[2015·陕西卷] 设 f(x)=ln x,0p
C.p=rq
10.C [解析] r=1
2(f(a)+f(b))=1
2ln(ab)=ln ab=p.因为 b>a>0,所以a+b
2
> ab,又函
数 f(x)在(0,+∞)上单调递增,所以 q>p=r,故选 C.
9.E5,E6[2015·四川卷] 设实数 x,y 满足
2x+y≤10,
x+2y≤14,
x+y≥6,
则 xy 的最大值为( )
A.25
2 B.49
2 C.12 D.16
9.A [解析] 画出可行域如图所示.可知当曲线 z=xy 与线段 AC 相切时 xy 取得最大
值.此时 2x+y=10,故 xy=1
2
·2x·y≤1
2
2x+y
2
2
=25
2
,当且仅当 x=5
2
,y=5 时取等号,
对应点落在线段 AC 上,故 xy 的最大值为25
2
,选 A.
14.E6[2015·重庆卷] 设 a,b>0,a+b=5,则 a+1+ b+3的最大值为________.
14 . 3 2 [ 解 析 ] ( a+1 + b+3 )2 = a + b + 4 + 2 a+1 · b+3 ≤ 9 +
2×( a+1)2+( b+3)2
2
=9+a+b+4=18,当且仅当 a+1=b+3 且 a+b=5,即 a=
7
2
,b=3
2
时等号成立,所以 a+1+ b+3≤3 2.
E7 不等式的证明方法
E8 不等式的综合应用
14.E8[2015·山东卷] 定义运算“ ”:x y=x2-y2
xy
(x,y∈R,xy≠0).当 x>0,y>0 时,
x y+(2y) x 的最小值为________.
14. 2 [解析] 由题意得 x y+(2y) x=x2-y2
xy
+4y2-x2
2xy
=2y2+x2
2xy
=y
x
+ x
2y
≥2 y
x
· x
2y
= 2,当且仅当 x= 2y 时,等号成立 .
E9 单元综合
4.[2015·浙江五校联考] 设 a,b 是实数,则“a>b>1”是“a+1
a>b+1
b
”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.A [解析] 因为 a+1
a
-b+1
b
=(a-b)(ab-1)
ab
,a>b>1,所以 a+1
a
-b+1
b
=
(a-b)(ab-1)
ab
>0,则充分性成立.当 a=1
2
,b=2
3
时,显然不等式 a+1
a>b+1
b
成立,但
a>b>1 不成立,所以必要性不成立.故选 A.
6.[2015·重庆一中模拟] 设对任意实数 x∈[-1,1],不等式 x2+ax-3a<0 恒成立,则
实数 a 的取值范围是( )
A.a>0 B.a>1
2
C.a>1
4 D.a>0 或 a<-12
6.B [解析] 设 f(x)=x2+ax-3a.
∵对任意实数 x∈[-1,1],不等式 x2+ax-3a<0 恒成立,
∴ f(-1)=1-a-3a<0,
f(1)=1+a-3a<0,
即 1-4a<0,
1-2a<0,
∴
a>1
4
,
a>1
2
,
故 a>1
2.
3.[2015·南昌调研] 若正数 a,b 满足1
a
+1
b
=1,则 4
a-1
+ 16
b-1
的最小值为( )
A.16 B.25
C.36 D.49
3 . A [ 解 析 ] 因 为 a>0 , b>0 , 1
a
+ 1
b
= 1 , 所 以 a + b = ab , 则 4
a-1
+ 16
b-1
=
4(b-1)+16(a-1)
(a-1)(b-1)
= 4b+16a-20
ab-(a+b)+1
=4b+16a-20.
又 4b+16a=4(b+4a)1
a
+1
b
=20+4b
a
+4a
b
≥20+4×2× b
a
·4a
b
=36,当且仅当b
a
=4a
b
且
1
a
+1
b
=1,即 a=3
2
,b=3 时取等号,所以 4
a-1
+ 16
b-1
≥36-20=16.
6.[2015·南充模拟] 若目标函数 z=ax+by(a>0,b>0)满足约束条件
2x-y-6≤0,
x-y+2≥0,
x≥0,y≥0,
且
最大值为 40,则5
a
+1
b
的最小值为( )
A.25
6 B.9
4 C.1 D.4
6.B [解析] 约束条件表示的平面区域如图中阴影部分所示,
当直线 z=ax+by(a>0,b>0)过直线 x-y+2=0 与直线 2x-y-6=0 的交点(8,10)时,
z 取得最大值 40,即 8a+10b=40,即 4a+5b=20,所以5
a
+1
b
=5
a
+1
b
×4a+5b
20
=5
4
+5b
4a
+ a
5b
≥
5
4
+1=9
4
,当且仅当 a=10
3
,b=4
3
时取等号.