无锡市2013年中考数学卷

无锡市2013年中考数学卷

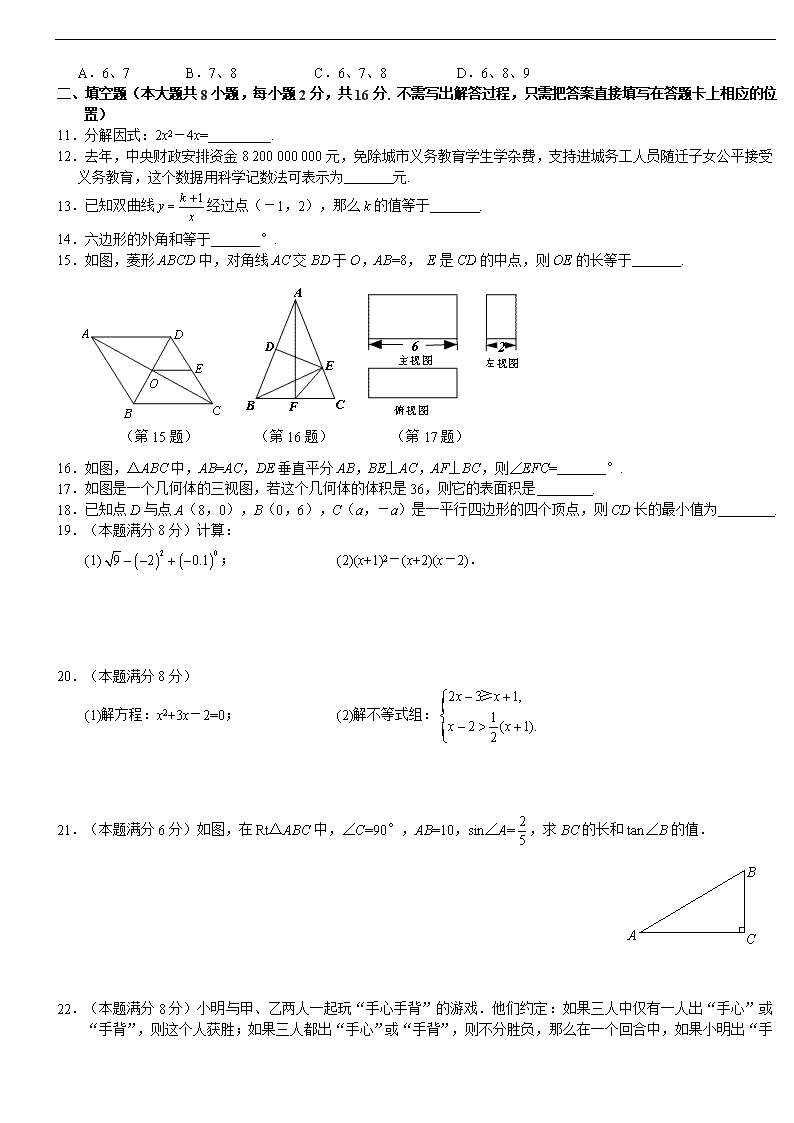
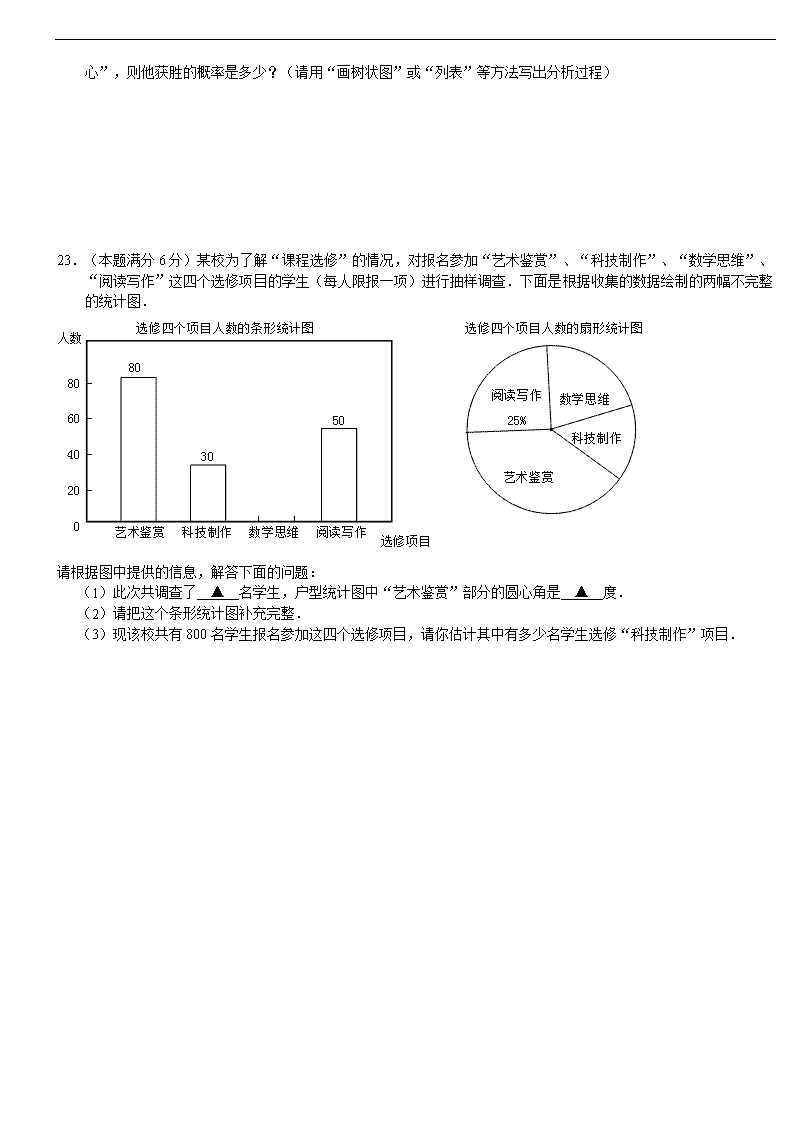
‎2013无锡市中考数学试卷 一、选择题（本大题共10小题,每小题3分,共30分．在每小题所给出的四个选项中,只有一项是正确的,请用2B铅笔把答题卡上相应的选项标号涂黑）‎ ‎1．的值等于 （ ▲ ）‎ ‎ A．2 B．‎-2 ‎ C． D．‎ ‎2．函数y=＋3中自变量的取值范围是 （ ▲ ）‎ ‎ A．x＞1 B．x ≥‎1 C．x≤1 D．‎ ‎3.方程的解为 （ ▲ ）‎ ‎ A． B． C． D．‎ ‎4.已知一组数据：15,13,15,16,17,16,14,15，则这组数据的极差与众数分别是（ ▲ ）‎ ‎ A．4,15 B．3,‎15 ‎ C．4,16 D．3,16‎ ‎5.下列说法中正确的是 （ ▲ ）‎ ‎ A．两直线被第三条直线所截得的同位角相等 ‎ B．两直线被第三条直线所截得的同旁内角互补 ‎ C．两平行线被第三条直线所截得的同位角的平分线互相垂直 ‎ D．两平行线被第三条直线所截得的同旁内角的平分线互相垂直 ‎6．已知圆柱的底面半径为‎3cm，母线长为‎5cm，则圆柱的侧面积是 （ ）‎ A．‎30cm2 B．30πcm‎2 ‎‎ C．‎15cm2 D．15πcm2 ‎ ‎7．如图，A、B、C是⊙O上的三点，且∠ABC=70°，则∠AOC的度数是 （ ）‎ A．35° B．140° C．70° D．70°或140°‎ ‎8．如图，梯形ABCD中，AD∥BC，对角线AC、BD相交于O，AD=1，BC=4，则△AOD与△BOC的面积比等于 （ ）‎ A． B． C． D．‎ ‎（第7题）‎ ‎（第8题）‎ ‎（第9题）‎ ‎9．如图，平行四边形ABCD中，AB∶BC=3∶2，∠DAB=60°，E在AB上，且AE∶EB=1∶2，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，则DP∶DQ等于 （ ）‎ A．3∶4 B．∶ C．∶ D．∶‎ ‎10．已知点A（0，0），B（0，4），C（3，t+4），D（3，t）. 记N（t）为□ABCD内部（不含边界）整点的个数，其中整点是指横坐标和纵坐标都是整数的点，则N（t）所有可能的值为 （ ）‎ A．6、7 B．7、‎8 ‎‎ C．6、7、8 D．6、8、9‎ 二、填空题（本大题共8小题，每小题2分，共16分. 不需写出解答过程，只需把答案直接填写在答题卡上相应的位置）‎ ‎11．分解因式：2x2－4x= .‎ ‎12．去年，中央财政安排资金8 200 000 000元，免除城市义务教育学生学杂费，支持进城务工人员随迁子女公平接受义务教育，这个数据用科学记数法可表示为 元.‎ ‎13．已知双曲线经过点（－1，2），那么k的值等于 .‎ ‎14．六边形的外角和等于 °.‎ ‎15．如图，菱形ABCD中，对角线AC交BD于O，AB=8， E是CD的中点，则OE的长等于 .‎ ‎ ‎‎（第15题）‎ ‎（第16题）‎ ‎（第17题）‎ ‎16．如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC= °.‎ ‎17．如图是一个几何体的三视图，若这个几何体的体积是36，则它的表面积是 .‎ ‎18．已知点D与点A（8，0），B（0，6），C（a，－a）是一平行四边形的四个顶点，则CD长的最小值为 .‎ ‎19．（本题满分8分）计算：‎ ‎ (1)； (2)(x+1)2－(x+2)(x－2)．‎ ‎20．（本题满分8分）‎ ‎ (1)解方程：x2+3x－2=0； (2)解不等式组：‎ ‎21．（本题满分6分）如图，在Rt△ABC中，∠C=90°，AB=10，sin∠A=，求BC的长和tan∠B的值．‎ B A C ‎22．（本题满分8分）小明与甲、乙两人一起玩“手心手背”的游戏．他们约定：如果三人中仅有一人出“手心”或“手背”，则这个人获胜；如果三人都出“手心”或“手背”，则不分胜负，那么在一个回合中，如果小明出“‎ 手心”，则他获胜的概率是多少？（请用“画树状图”或“列表”等方法写出分析过程）‎ ‎23．（本题满分6分）某校为了解“课程选修”的情况，对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生（每人限报一项）进行抽样调查．下面是根据收集的数据绘制的两幅不完整的统计图．‎ 请根据图中提供的信息，解答下面的问题：‎ ‎（1）此次共调查了 ▲ 名学生，户型统计图中“艺术鉴赏”部分的圆心角是 ▲ 度．‎ ‎（2）请把这个条形统计图补充完整．‎ ‎（3）现该校共有800名学生报名参加这四个选修项目，请你估计其中有多少名学生选修“科技制作”项目．‎ ‎24．（本题满分10分）如图，四边形ABCD中，对角线AC与BD相交于O，在①AB∥CD；②AO＝CO；③AD＝BC中任意选取两个作为条件，“四边形ABCD是平行四边形”为结论构成命题．‎ ‎（1）以①②作为条件构成的命题是真命题吗？若是，请证明；若不是，请举出反例；‎ ‎（2）写出按题意构成的所有命题中的假命题，并举出反例加以说明．（命题请写成“如果…，那么…．”的形式）‎ ‎25．（本题满分8分）已知甲、乙两种原料中均含有A元素，其含量及每吨原料的购买单价如下表所示：‎ A元素含量 单价（万元/吨）‎ 甲原料 ‎5%‎ ‎2.5‎ 乙原料 ‎8%‎ ‎6‎ 已知用甲原料提取每千克A元素要排放废气1吨，用乙原料提取每千克A元素要排放废气0.5吨．若某厂要提取A元素‎20千克，并要求废气排放不超过16吨，问：该厂购买这两种原料的费用最少是多少万元？‎ ‎26．（本题满分10分）如图，直线x＝－4与x轴交于E，一开口向上的抛物线过原点O交线段OE于A，交直线x＝－4于B．过B且平行于x轴的直线与抛物线交于C，直线OC交直线AB于D，且AD:BD＝1:3．‎ ‎（1）求点A的坐标；‎ ‎（2）若△OBC是等腰三角形，求此抛物线的函数关系式．‎ ‎27．（本题满分10分）如图1，菱形ABCD中，∠A=600．点P从A出发，以‎2cm/s的速度沿边AB、BC、CD匀速运动到D终止；点Q从A与P同时出发，沿边AD匀速运动到D终止，设点P运动的时间为t s．△APQ的面积s(cm2)与t(s)之间函数关系的图像由图2中的曲线段OE与线段EF、FG给出．‎ ‎（图1）‎ ‎（图2）‎ ‎ (1)求点Q运动的速度；‎ ‎ (2)求图2中线段FG的函数关系式；‎ ‎(3)问：是否存在这样的t，使PQ将菱形ABCD的面积恰好分成1:5的两部分？若存在，求出这样的t的值；若不存在，请说明理由．‎ ‎28．（本题满分10分）下面给出的正多边形的边长都是‎20 cm．请分别按下列要求设计一种剪拼方法（用虚线表示你的设计方案，把剪拼线段用粗黑实线，在图中标注出必要的符号和数据，并作简要说明．‎ ‎（1）将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型，使它的表面积与原正方形面积相等；‎ ‎（2）将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型，使它的表面积与原正三角形的面积相等；‎ ‎（3）将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型，使它的表面积与原正五边形的面积相等．‎ ‎（图1）‎ ‎（图2）‎ ‎（图3）‎