2008年湖北省高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】

2008年湖北省高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】

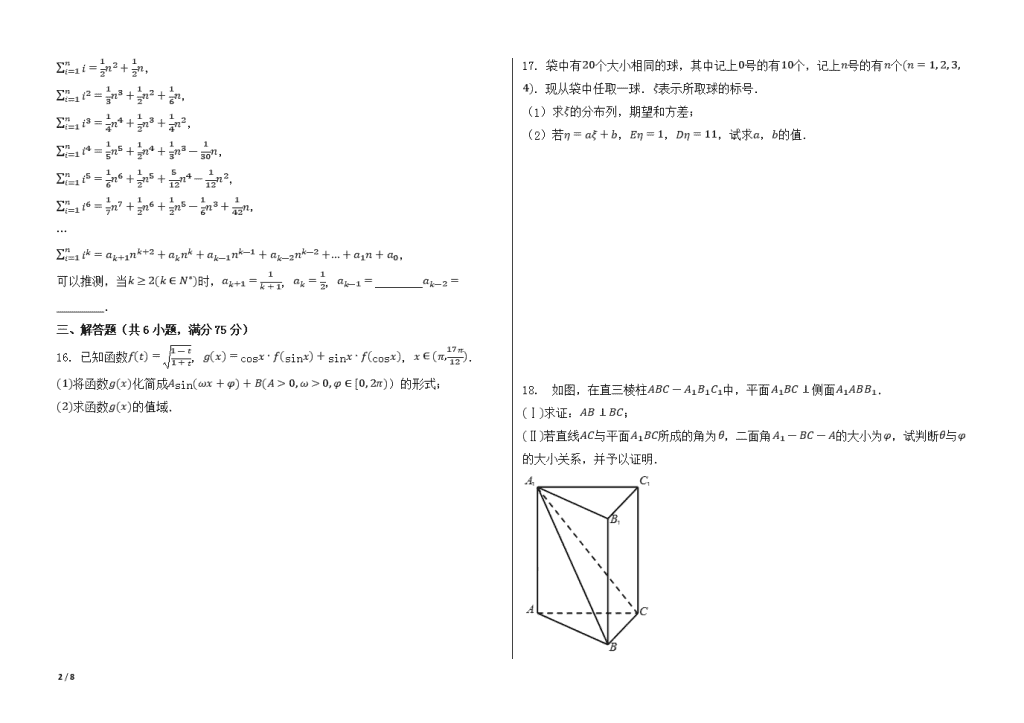
‎2008年湖北省高考数学试卷（理科）‎ 一、选择题（共10小题，每小题5分，满分50分）‎ ‎1. 设a‎→‎‎=(1, -2)‎，b‎→‎‎=(-3, 4)‎，c‎→‎‎=(3, 2)‎则‎(a‎→‎+2b‎→‎)⋅c‎→‎=(‎ ‎‎)‎ A.‎(-15, 12)‎ B.‎0‎ C.‎-3‎ D.‎‎-11‎ ‎2. 若非空集合A，B，C满足A∪B＝C，且B不是A的子集，则（ ）‎ A.“x∈C”是“x∈A”的充分条件但不是必要条件 B.“x∈C”是“x∈A”的必要条件但不是充分条件 C.“x∈C”是“x∈A”的充要条件 D.“x∈C”既不是“x∈A”的充分条件也不是“x∈A”必要条件 ‎3. 用与球心距离为‎1‎的平面去截球，所得的截面面积为π，则球的体积为(        )‎ A.‎8π‎3‎ B.‎8‎2‎π‎3‎ C.‎8‎2‎π D.‎‎32π‎3‎ ‎4. 函数f(x)=‎1‎xln(x‎2‎‎-3x+2‎+‎-x‎2‎-3x+4‎)‎的定义域为（ ）‎ A.‎(-∞, -4]∪[2, +∞)‎ B.‎‎(-4, 0)∪(0.1)‎ C.‎[-4, 0)∪(0, 1]‎ D.‎‎[-4, 0)∪(0, 1)‎ ‎5. 将函数y=sin(x-θ)‎的图象F向右平移π‎3‎个单位长度得到图象F'‎，若F'‎的一条对称轴是直线x=‎π‎4‎则θ的一个可能取值是（ ）‎ A.‎5‎‎12‎π B.‎-‎5‎‎12‎π C.‎11‎‎12‎π D.‎‎-‎11‎‎12‎π ‎6. 将‎5‎名志愿者分配到‎3‎个不同的奥运场馆参加接待工作，每个场馆至少分配一名志愿者的方案种数为(        )‎ A.‎540‎ B.‎300‎ C.‎180‎ D.‎‎150‎ ‎7. 若f(x)=-‎1‎‎2‎x‎2‎+bln(x+2)‎在‎(-1, +∞)‎上是减函数，则b的取值范围是（ ）‎ A.‎[-1, +∞)‎ B.‎(-1, +∞)‎ C.‎(-∞, -1]‎ D.‎‎(-∞, -1)‎ ‎8. 已知m∈‎N‎*‎，a，b∈R，若limx→0‎‎(1+x‎)‎m+ax‎=b，则a⋅b=(‎ ‎‎)‎ A.‎-m B.m C.‎-1‎ D.‎‎1‎ ‎9. 过点A(11, 2)‎作圆x‎2‎‎+y‎2‎+2x-4y-164‎＝‎0‎的弦，其中弦长为整数的共有（ ）‎ A.‎16‎条 B.‎17‎条 C.‎32‎条 D.‎34‎条 ‎10. 如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道I绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行，最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行，若用‎2‎c‎1‎和‎2‎c‎2‎分别表示椭圆轨道I和II的焦距，用‎2‎a‎1‎和‎2‎a‎2‎分别表示椭圆轨道I和II的长轴的长，给出下列式子：‎ ‎①a‎1‎‎+c‎1‎=a‎2‎+‎c‎2‎；②a‎1‎‎-c‎1‎=a‎2‎-‎c‎2‎；③c‎1‎a‎2‎‎>‎a‎1‎c‎2‎；④c‎1‎a‎1‎‎<‎c‎2‎a‎2‎．‎ 其中正确式子的序号是（ ）‎ A.①③ B.②③ C.①④ D.②④‎ 二、填空题（共5小题，每小题5分，满分25分）‎ ‎11. 设z‎1‎是复数，z‎2‎‎=z‎1‎-iZ‎¯‎‎1‎，（其中Z‎¯‎‎1‎表示z‎1‎的共轭复数），已知z‎2‎的实部是‎-1‎，则z‎2‎的虚部为________．‎ ‎12. 在‎△ABC中，三个角A，B，C的对边边长分别为a=3‎，b=4‎，c=6‎，则bccosA+cacosB+abcosC的值为________．‎ ‎13. 已知函数f(x)=x‎2‎+2x+a，f(bx)=9x‎2‎-6x+2‎，其中x∈R，a，b为常数，则方程f(ax+b)=0‎的解集为________．‎ ‎14. 已知函数f(x)=‎‎2‎x，等差数列‎{ax}‎的公差为‎2‎．若f(a‎2‎+a‎4‎+a‎6‎+a‎8‎+a‎10‎)=4‎，则log‎2‎‎[f(a‎1‎)⋅f(a‎2‎)⋅f(a‎3‎)⋅...⋅f(a‎10‎)]=‎________．‎ ‎15. 观察下列等式：‎ ‎ 8 / 8‎ i=1‎ni‎=‎1‎‎2‎n‎2‎+‎1‎‎2‎n‎，‎ i=1‎ni‎2‎‎=‎1‎‎3‎n‎3‎+‎1‎‎2‎n‎2‎+‎1‎‎6‎n‎，‎ i=1‎ni‎3‎‎=‎1‎‎4‎n‎4‎+‎1‎‎2‎n‎3‎+‎‎1‎‎4‎n‎2‎‎，‎ i=1‎ni‎4‎‎=‎1‎‎5‎n‎5‎+‎1‎‎2‎n‎4‎+‎1‎‎3‎n‎3‎-‎1‎‎30‎n‎，‎ i=1‎ni‎5‎‎=‎1‎‎6‎n‎6‎+‎1‎‎2‎n‎5‎+‎5‎‎12‎n‎4‎-‎‎1‎‎12‎n‎2‎‎，‎ i=1‎ni‎6‎‎=‎1‎‎7‎n‎7‎+‎1‎‎2‎n‎6‎+‎1‎‎2‎n‎5‎-‎1‎‎6‎n‎3‎+‎1‎‎42‎n‎，‎ ‎…‎ i=1‎nik‎=ak+1‎nk+2‎+aknk+ak-1‎nk-1‎+ak-2‎nk-2‎+…+a‎1‎n+‎a‎0‎‎，‎ 可以推测，当k≥2(k∈N‎*‎)‎时，ak+1‎‎=‎1‎k+1‎，ak=‎1‎‎2‎，ak-1‎=‎________ak-2‎‎=‎________．‎ 三、解答题（共6小题，满分75分）‎ ‎16. 已知函数f(t)=‎1-t‎1+t，g(x)=cosx⋅f(sinx)+sinx⋅f(cosx)，x∈(π,‎17π‎12‎)‎．‎ ‎(1)‎将函数g(x)‎化简成Asin(ωx+φ)+B(A>0, ω>0, φ∈[0, 2π)‎）的形式；‎ ‎(2)‎求函数g(x)‎的值域．‎ ‎17. 袋中有‎20‎个大小相同的球，其中记上‎0‎号的有‎10‎个，记上n号的有n个‎(n=1, 2, 3, 4)‎．现从袋中任取一球．ξ表示所取球的标号．‎ ‎（1）求ξ的分布列，期望和方差；‎ ‎（2）若η=aξ+b，Eη=1‎，Dη=11‎，试求a，b的值．‎ ‎18. 如图，在直三棱柱ABC-‎A‎1‎B‎1‎C‎1‎中，平面A‎1‎BC⊥‎侧面A‎1‎ABB‎1‎．‎ ‎(‎Ⅰ‎)‎求证：AB⊥BC；‎ ‎(‎Ⅱ‎)‎若直线AC与平面A‎1‎BC所成的角为θ，二面角A‎1‎‎-BC-A的大小为φ，试判断θ与φ的大小关系，并予以证明．‎ ‎ 8 / 8‎ ‎19. 如图，在以点O为圆心，‎|AB|=4‎为直径的半圆ADB中，OD⊥AB，P是半圆弧上一点，‎∠POB=‎‎30‎‎∘‎，曲线C是满足‎||MA|-|MB||‎为定值的动点M的轨迹，且曲线C过点P．‎ ‎（1）建立适当的平面直角坐标系，求曲线C的方程；‎ ‎（2）设过点D的直线l与曲线C相交于不同的两点E、F．若‎△OEF的面积不小于‎2‎‎2‎，求直线l斜率的取值范围．‎ ‎20. 水库的蓄水量随时间而变化，现用t表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于t的近似函数关系式为V(t)=‎‎(-t‎2‎+14t-40)e‎1‎‎4‎x+50‎‎00,‎AC‎→‎与n的夹角β为锐角，则β与θ互为余角．sinθ-cosβ=n⋅‎AC‎→‎‎|n|⋅|AC‎→‎|‎=‎acba‎2‎‎+‎c‎2‎，cosφ=BA‎1‎‎→‎‎⋅‎BA‎→‎‎|BA‎1‎‎→‎|⋅|BA‎→‎|‎=‎ca‎2‎‎+‎c‎2‎，‎ 所以sinφ=‎aa‎2‎‎+‎c‎2‎，‎ 于是由c0‎‎⇔‎k≠±1‎‎-‎3‎0‎，‎ 解得t<4‎，或t>10‎，又‎03a存在实数λ，使得对任意正整数n，都有a

查看更多