- 2021-04-15 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届新高考版高考数学一轮复习课件:§7-1 平面向量的概念、线性运算及基本定理(讲解部分)
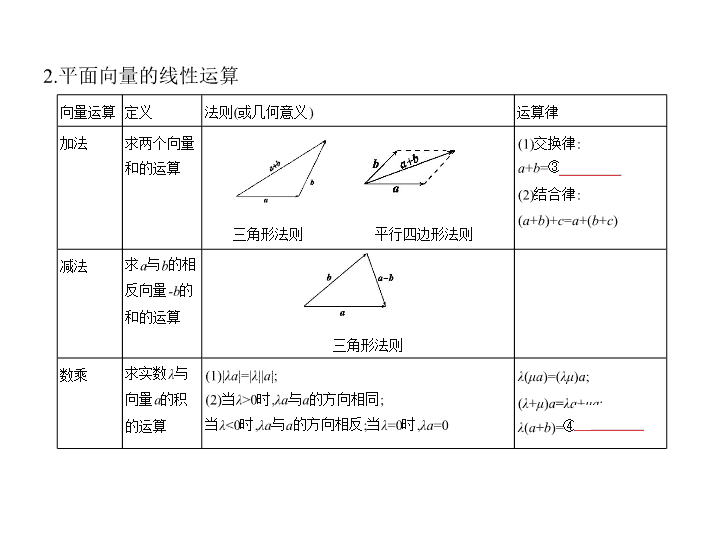
第七章 平面向量 §7.1 平面向量的概念、线性运算及基本定理 高考数学 考点一 平面向量的概念及线性运算 1.向量的有关概念及表示法 考点清单 名称 定义 表示法 向量 既有大小又有方向的量叫向量;向量的大小叫做向量的长度(或模) 向量: ;模:① | | 零向量 长度为0的向量叫零向量,其方向是任意的 记作0 单位向量 长度等于1个单位的向量 常用 e 表示 平行向量 方向相同或相反的非零向量 a 与 b 共线可记为② a ∥ b ;0与任一向量共线 共线向量 平行向量又叫做共线向量 相等向量 长度相等且方向相同的向量 a = b 相反向量 长度相等且方向相反的向量 a 与 b 互为相反向量,则 a =- b ;0的相反向量为0 2.平面向量的线性运算 向量运算 定义 法则(或几何意义) 运算律 加法 求两个向量和的运算 三角形法则 平行四边形法则 (1)交换律: a + b =③ b + a ; (2)结合律: ( a + b )+ c = a +( b + c ) 减法 求 a 与 b 的相反向量- b 的 和的运算 三角形法则 数乘 求实数 λ 与向量 a 的积 的运算 (1)| λa |=| λ || a |; (2)当 λ >0时, λa 与 a 的方向相同; 当 λ <0时, λa 与 a 的方向相反;当 λ =0时, λa =0 λ ( μa )=( λμ ) a ; ( λ + μ ) a = λa + μa ; λ ( a + b )=④ λa + λb 考点二 平面向量基本定理及坐标运算 1.共线向量定理 (1)判定定理: a 是一个非零向量,若存在一个实数 λ 使得⑤ b = λa ,则向量 b 与 a 共线. (2)性质定理:若向量 b 与非零向量 a 共线,则存在唯一一个实数 λ ,使得 b = λa . (3) A , B , C 是平面上三点,且 A 与 B 不重合, P 是平面内任意一点,若点 C 在直线 AB 上,则存在实数 λ ,使得 =(1- λ ) + λ ,如图. 如果 e 1 、 e 2 是同一平面内的两个不共线向量,那么对于这一平面内的任意 向量 a ,有且只有一对实数 λ 1 、 λ 2 ,使 a = λ 1 e 1 + λ 2 e 2 . 其中,⑥ 不共线 的向量 e 1 、 e 2 叫做表示这一平面内所有向量的一组基底. 2.平面向量基本定理 温馨提示 (1)构成基底的两向量不共线; (2)基底给定,同一向量的分解形式唯一; (3)若 λ 1 e 1 + λ 2 e 2 =0,则 λ 1 = λ 2 =0. 3.平面向量的坐标表示 (1)在平面直角坐标系中,分别取与 x 轴、 y 轴方向相同的两个单位向量 i 、 j 作为基底.对于平面内的一个向量 a ,由平面向量基本定理知,有且只有一对 实数 x 、 y ,使得 a = xi + yj ,这样,平面内的任一向量 a 都可由 x 、 y 唯一确定,我们 把有序数对⑦ ( x , y ) 叫做向量 a 的坐标,记作 a =( x , y ),其中 x 叫做 a 在 x 轴上 的坐标, y 叫做 a 在 y 轴上的坐标,显然0=(0,0), i =(1,0), j =⑧ (0,1) . (2)设 = xi + yj ,则向量 的坐标( x , y )就是终点 A 的坐标,即若 =( x , y ),则 A 点坐标为⑨ ( x , y ) ,反之亦成立( O 是坐标原点). 4.向量的坐标运算 (1)平面向量运算的坐标表示 坐标表示 加法 已知 a =( x 1 , y 1 ), b =( x 2 , y 2 ),则 a + b =⑩ ( x 1 + x 2 , y 1 + y 2 ) 减法 已知 a =( x 1 , y 1 ), b =( x 2 , y 2 ),则 a - b = ( x 1 - x 2 , y 1 - y 2 ) 数乘 已知 a =( x 1 , y 1 ),则 λa = ( λx 1 , λy 1 ) ,其中 λ 是实数 任一向量 的坐标 已知 A ( x 1 , y 1 ), B ( x 2 , y 2 ),则 = ( x 2 - x 1 , y 2 - y 1 ) 温馨提示 a.向量相等,则坐标相同;b.向量的坐标与表示该向量的有向线 段的始点、终点的具体位置无关,只与其相对位置有关. (2)平面向量共线的坐标表示:若 a =( x 1 , y 1 ), b =( x 2 , y 2 ),则 a ∥ b ⇔ x 1 y 2 - x 2 y 1 =0. 温馨提示 a.若 a =( x 1 , y 1 ), b =( x 2 , y 2 ),则 a ∥ b 的充要条件不能表示成 = .因 为 x 2 , y 2 有可能等于0,所以应表示为 x 1 y 2 - x 2 y 1 =0.同时, a ∥ b 的充要条件也不能 错记为 x 1 x 2 - y 1 y 2 =0, x 1 y 1 - x 2 y 2 =0等. b.若 a =( x 1 , y 1 ), b =( x 2 , y 2 ),则 a ∥ b 的充要条件是 a = λb ( b ≠ 0),这与 x 1 y 2 - x 2 y 1 =0在本 质上是没有差异的,只是形式上不同. 考法一 与平面向量线性运算有关的解题策略 知能拓展 例1 (2019豫南九校第三次联考,8)如图所示,在△ ABC 中,点 M 是 AB 的中 点,且 = , BN 与 CM 相交于点 E ,设 = a , = b ,则 等于 ( ) A. a + b B. a + b C. a + b D. a + b 解题导引 由条件 BN 与 CM 相交于点 E ,可知 N , E , B 三点共线及 C , E , M 三点共线,由共线向量定理可设 = m +(1- m ) , = n +(1- n ) ,再利用 = , = ,结合平面向量基本定理建立关系式,求得 m 、 n 的值,进而表示出 . 解析 由题意得 = = b , = = a , 由 N , E , B 三点共线可知,存在实数 m ,满足 = m +(1- m ) = mb +(1- m ) a . 由 C , E , M 三点共线可知,存在实数 n ,满足 = n +(1- n ) = na +(1- n ) b ,所 以 mb +(1- m ) a = na +(1- n ) b , 因为 a , b 为基底,所以 解得 所以 = a + b ,故选A. 答案 A 例2 (2019河北3月质检,6)在△ ABC 中, O 为△ ABC 的重心.若 = λ + μ ,则 λ -2 μ = ( ) A.- B.-1 C. D.- 解题导引 三角形重心有什么性质?重心 O 是△ ABC 中什么线的交点?(中 线交点)延长 BO 交 AC 于点 M ,由重心的性质可知, M 为 AC 的中点,且 = ,再把 用 , 表示出来,得出 λ , μ 的值,进而可得 λ -2 μ . 解析 如图,延长 BO 交 AC 于点 M ,∵点 O 为△ ABC 的重心,∴ M 为 AC 的中点,∴ = = =- + =- + ( - )=- + ,又 = λ + μ ,∴ λ =- , μ = ,∴ λ -2 μ =- -2 × =- ,故选D. 答案 D 方法总结 1.若 A , B , P 三点共线,则可设成 = λ 的形式,也可以设成 = t +(1- t ) 的形式,两种设法因题而异,如例1,就用到了第二种设法;2.用几 个基本向量表示某个向量问题的基本技巧:(1)观察各向量的位置;(2)寻找 相应的三角形或多边形;(3)运用法则找关系;(4)化简结果. 考法二 与平面向量坐标运算有关的解题策略 例3 (2018湘东五校4月联考,15)在正方形 ABCD 中, M , N 分别是 BC , CD 的中 点,若 = λ + μ ,则实数 λ + μ = . 解题导引 分别以 AB , AD 所在直线为 x , y 轴建立平面直角坐标系,设正方形 的边长为2,然后写出 A , M , N , C 的坐标,利用平面向量的坐标运算求解. 解析 分别以 AB , AD 所在直线为 x , y 轴建立平面直角坐标系,如图, A (0,0). 设正方形的边长为2,则 C (2,2), ∵ M , N 分别是 BC , CD 的中点, ∴ M (2,1), N (1,2), ∴ =(2,2), =(1,2), =(2,1), 又∵ = λ + μ ,∴(2,2)= λ (2,1)+ μ (1,2), ∴ ∴ ∴ λ + μ = . 答案 例4 (2019河北邯郸重点中学9月联考,11)给定两个长度为1的平面向量 和 ,它们的夹角为120 ° ,点 C 在以 O 为圆心的圆弧 AB 上运动,若 = x + y ,则 x + y 的最大值是 ( ) A. B.1 C. D.2 解题导引 由于点 C 在 上运动,故可设∠ AOC = θ ,再通过建 系,求点 A , B , C 的坐标,结合 = x + y ,将 x , y 用 θ 表示出来,进而求出 x + y 的最大值. 解析 以 O 为原点, OA 所在直线为 x 轴建立平面直角坐标系,如图所示, 设∠ AOC = θ , 易知, A (1,0), B , C (cos θ ,sin θ ) . ∵ = x + y ,∴ ∴ ∴ x + y = sin θ +cos θ + sin θ = sin θ +cos θ =2sin .又0 ≤ θ ≤ , ∴sin ∈ ,∴当 θ = 时, x + y 取最大值2,故选D. 答案 D 方法总结 在解决圆、直角三角形、矩形等特殊图形中的向量问题时,建 立合适的平面直角坐标系可以快速打开思路.查看更多