高考数学专题复习练习第二章 第五节 函数的图象 课下练兵场

申明敬告： 本站不保证该用户上传的文档完整性，不预览、不比对内容而直接下载产生的反悔问题本站不予受理。

文档介绍

高考数学专题复习练习第二章 第五节 函数的图象 课下练兵场

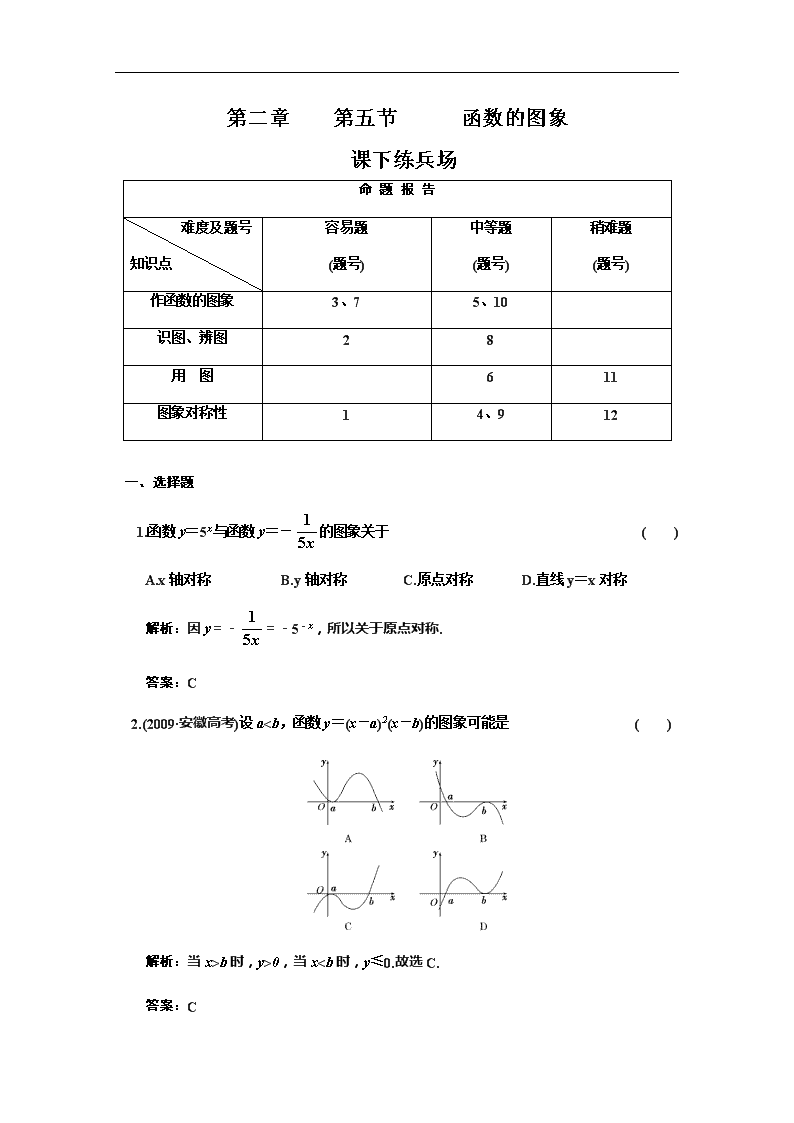
第二章 第五节 函数的图象 课下练兵场 命 题 报 告 ‎ 难度及题号 知识点 容易题 ‎(题号)‎ 中等题 ‎(题号)‎ 稍难题 ‎(题号)‎ 作函数的图象 ‎3、7‎ ‎5、10‎ 识图、辨图 ‎2‎ ‎8‎ 用　图 ‎6‎ ‎11‎ 图象对称性 ‎1‎ ‎4、9‎ ‎12‎ 一、选择题 ‎1.函数y＝5x与函数y＝－的图象关于 (　　)‎ A.x轴对称　　　　　B.y轴对称 C.原点对称 D.直线y＝x对称 解析：因y＝－＝－5－x，所以关于原点对称.‎ 答案：C ‎2.(2009·安徽高考)设ab时，y>0，当x1)的图象关于原点对称，则函数g(x)的大致图象是下列图象中的 (　　)‎ 解析：先作出f(x)＝lg x的图象，再向右平移1个单位长度，得到f(x)＝lg(x－1)的图象，再作所得图象关于原点对称的图象，得到B选项. ‎ 答案：B ‎6.(2010·平顶山模拟)f(x)的定义域为R，且f(x)＝若方程f(x)＝x＋a有两不同实根，则a的取值范围为 (　　)‎ A.(－∞，1) B.(－∞，1] C.(0,1) D.(－∞，＋∞)‎ 解析：x≤0时，f(x)＝2－x－1，‎ ‎0＜x≤1时，－1＜x－1≤0，‎ f(x)＝f(x－1)＝2－(x－1)－1.‎ 故x＞0时，f(x)是周期函数，如图，‎ 欲使方程f(x)＝x＋a有两解，‎ 即函数f(x)的图象与直线y＝x＋a有两个不同交点，‎ 故a＜1，则a的取值范围是(－∞，1).‎ 答案：A 二、填空题 ‎7.为了得到函数f(x)＝log2x的图象，只需将函数g(x)＝log2的图象　　　　　　　　　.‎ 解析：g(x)＝log2＝log2x－3＝f(x)－3，因此只需将函数g(x)的图象向上平移3个单位即可得到函数f(x)＝log2x的图象.‎ 答案：向上平移3个单位 ‎8.已知下列曲线：‎ 以及编号为①②③④的四个方程：‎ ‎①－＝0；②|x|－|y|＝0；③x－|y|＝0；④|x|－y＝0.‎ 请按曲线A、B、C、D的顺序，依次写出与之对应的方程的编号　　　　.‎ 解析：按图像逐个分析，注意x、y的取值范围.‎ 答案：④②①③‎ ‎9.给出如下三个函数：①f(x)＝(x－1)3；②f(x)＝k(x－1) (k<0) ; ③‎ 则同时满足性质：(1)对于任意的x1，x2∈R(x1≠x2)，有>0；(2)图象关于点(1,0)‎ 成中心对称图形的函数序号为　　　　.‎ 解析：f(x)＝(x－1)3可以看成f(x)＝x3向右平移一个单位得到的函数.‎ 又>0，则f(x)为增函数.故只有①满足.‎ 答案：①‎ 三、解答题 ‎10.作出下列函数的图象：‎ ‎(1)y＝10|lgx|；‎ ‎(2)y＝x－|x－1|.‎ 解：（1）因 当x≥1时，10|lgx|＝10lgx＝x；‎ 当0
查看更多

相关文章

您可能关注的文档