- 2021-04-15 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习(精选精讲)练习7-简单几何体习题精选精讲
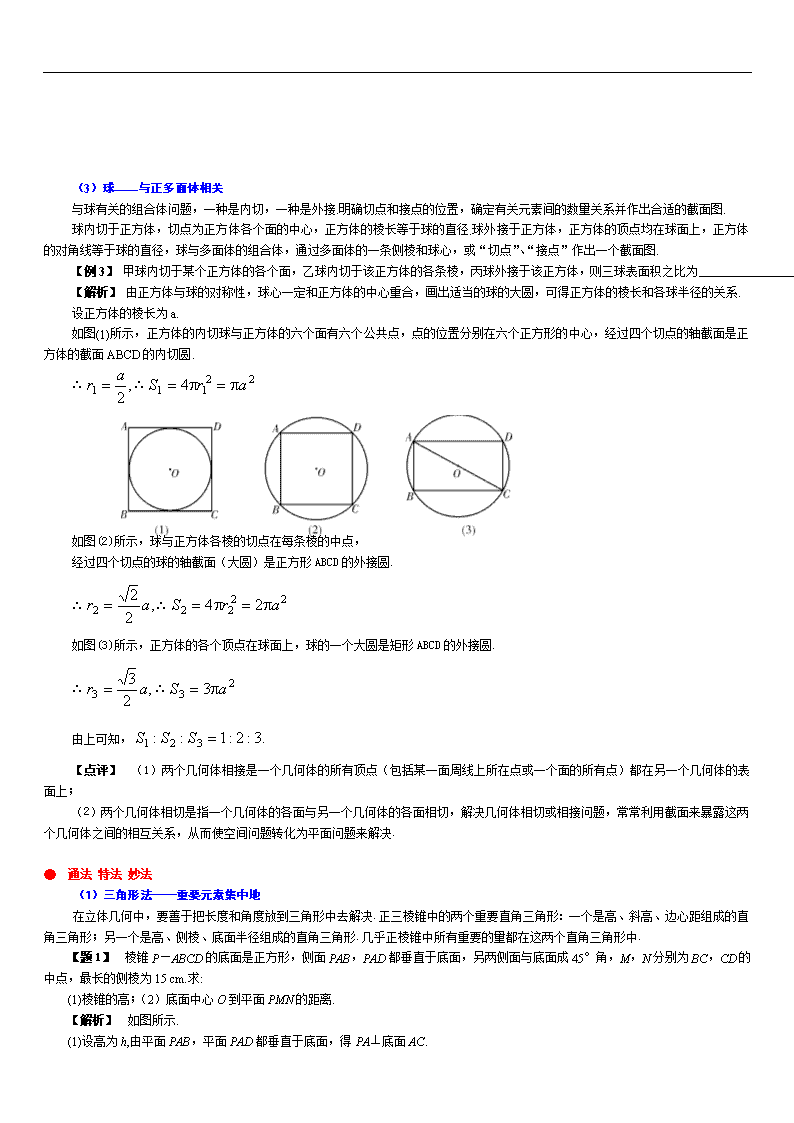
简单几何体 (1)棱柱——最常见的多面体 空间直线与平面的只研究位置关系,没有大小和形状的研究;而具体的几何体除位置关系外,还有大小和形状的区别. 几何体按形状分两大类:一是由平面围成的多面体,如正方体;二是由曲面围成的旋转体,如球. 棱柱是常见的多面体,它有两个本质属性:①有两个面(底面)互相平行;②其余各面(侧面)每相邻两个面的公共边(侧棱)都互相平行. A B C D E A1 B1 C1 棱柱在高考中是常考的一种载体,除考查空间线面关系(空间角和距离)外,还有面积、体积计算问题的考查. 【例1】如图,在直三棱柱ABC-A1B1C1中,AB=BC, D、E分别为BB1、AC1的中点. (Ⅰ)证明:ED为异面直线BB1与AC1的公垂线; (Ⅱ)设AA1=AC=AB,求二面角A1-AD-C1的大小. 【解析1】(Ⅰ)设O为AC中点,连接EO,BO, A B C D E A1 B1 C1 O F 则EOC1C,又C1CB1B,所以EODB, EOBD为平行四边形,ED∥OB. ∵AB=BC,∴BO⊥AC, 又平面ABC⊥平面ACC1A1,BO Ì 面ABC, 故BO⊥平面ACC1A1, ∴ED⊥平面ACC1A1,BD⊥AC1,ED⊥CC1, ∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线. (Ⅱ)连接A1E,由AA1=AC=AB可知,A1ACC1为正方形, ∴A1E⊥AC1,又由ED⊥平面ACC1A1和EDÌ平面ADC1知平面 ADC1⊥平面A1ACC1,∴A1E⊥平面ADC1.作EF⊥AD,垂足为F,连接A1F,则A1F⊥AD,∠A1FE为二面角A1-AD-C1的平面角. 不妨设AA1=2,则AC=2,AB=ED=OB=1,EF==, tan∠A1FE=,∴∠A1FE=60°. 所以二面角A1-AD-C1为60°. 【解析2】(Ⅰ)如图,建立直角坐标系O-xyz,其中原点O为AC的中点. 设A(a,0,0),B(0,b,0),B1(0,b,2c). 则C(-a,0,0),C1(-a,0,2c),E(0,0,c),D(0,b,c). A B C D E A1 B1 C1 O z x y =(0,b,0),=(0,0,2c). ·=0,∴ED⊥BB1. 又=(-2a,0,2c), ·=0,∴ED⊥AC1, 所以ED是异面直线BB1与AC1的公垂线. (Ⅱ)不妨设A(1,0,0),则B(0,1,0),C(-1,0,0),A1(1,0,2), =(-1,-1,0),=(-1,1,0),=(0,0,2), ·=0,·=0,即BC⊥AB,BC⊥AA1,又AB∩AA1=A, ∴BC⊥平面A1AD. 又 E(0,0,1),D(0,1,1),C(-1,0,1), =(-1,0,-1),=(-1,0,1),=(0,1,0), ·=0,·=0,即EC⊥AE,EC⊥ED,又AE∩ED=E, ∴ EC⊥面C1AD. cos<,>==,即得和的夹角为60°. 所以二面角A1-AD-C1为60°. (2)棱锥——最简单的多面体 棱锥是一种简单的多面体,它有两个主要特征:①有一个形状是多边形的底面;②其他各面是有一个公共顶点的三角形,这些三角形是棱锥的侧面. 三棱锥是最简单的棱锥,也是最简单的多面体(四面体),多面体的研究往往归结到三棱锥来,正像多边形的研究要归结到三角形一样. 三棱锥常成为多面体考题的载体. 故有人说,考多面体说到底是在考三棱锥. 【例2】 (I)给出两块相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明; (II)试比较你剪拼的正三棱锥与正三棱柱的体积的大小; (III)如果给出的是一块任意三角形的纸片(如图3),要求剪栟成一个直三棱柱,使它的全面积与给出的三角形的面积相等。请设计一种剪拼方法,用虚线标示在图3中,并作简要说明。 【解析】解(I)如图1,沿正三角形三边中点连线折起,可拼得一个正三棱锥. 如图2,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的,有一组对角为直角,余下部分按虚线折起,可成一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱锥的上底. (II)依上面剪拼方法,有. 推理如下: 设给出正三角形纸片的边长为2,那么,正三棱锥与正三棱柱的底面都是边长为1的正三角形,其面积为.现在计算它们的高: ,. 所以. (III)如图3,分别连结三角形的内心与各顶点,得三条线段,再以这三条线段的中点为顶点作三角形.以新作的三角形为直棱柱的底面,过新三角形的三个顶点向原三角形三边作垂线,沿六条垂线剪下三个四边形,可心拼成直三棱柱的上底,余下部分按虚线折起,成为一个缺上底的直三棱柱,即可得到直三棱柱. (3)球——与正多面体相关 与球有关的组合体问题,一种是内切,一种是外接.明确切点和接点的位置,确定有关元素间的数量关系并作出合适的截面图. 球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径.球外接于正方体,正方体的顶点均在球面上,正方体的对角线等于球的直径,球与多面体的组合体,通过多面体的一条侧棱和球心,或“切点”、“接点”作出一个截面图. 【例3】 甲球内切于某个正方体的各个面,乙球内切于该正方体的各条棱,丙球外接于该正方体,则三球表面积之比为 . 【解析】 由正方体与球的对称性,球心一定和正方体的中心重合,画出适当的球的大圆,可得正方体的棱长和各球半径的关系. 设正方体的棱长为a. 如图(1)所示,正方体的内切球与正方体的六个面有六个公共点,点的位置分别在六个正方形的中心,经过四个切点的轴截面是正方体的截面ABCD的内切圆. ∴∴ 如图(2)所示,球与正方体各棱的切点在每条棱的中点, 经过四个切点的球的轴截面(大圆)是正方形ABCD的外接圆. ∴∴ 如图(3)所示,正方体的各个顶点在球面上,球的一个大圆是矩形ABCD的外接圆. ∴∴ 由上可知, 【点评】 (1)两个几何体相接是一个几何体的所有顶点(包括某一面周线上所在点或一个面的所有点)都在另一个几何体的表面上; (2)两个几何体相切是指一个几何体的各面与另一个几何体的各面相切,解决几何体相切或相接问题,常常利用截面来暴露这两个几何体之间的相互关系,从而使空间问题转化为平面问题来解决. ● 通法 特法 妙法 (1)三角形法——重要元素集中地 在立体几何中,要善于把长度和角度放到三角形中去解决.正三棱锥中的两个重要直角三角形:一个是高、斜高、边心距组成的直角三角形;另一个是高、侧棱、底面半径组成的直角三角形.几乎正棱锥中所有重要的量都在这两个直角三角形中. 【题1】 棱锥P—ABCD的底面是正方形,侧面PAB,PAD都垂直于底面,另两侧面与底面成45°角,M,N分别为BC,CD的中点,最长的侧棱为15 cm.求: (1)棱锥的高;(2)底面中心O到平面PMN的距离. 【解析】 如图所示. (1)设高为h,由平面PAB,平面PAD都垂直于底面,得PA⊥底面AC. 又∠PBA=45°,∴PA=AB=h,AC=h . 由PA2+AC2=PC2及PC=15, 得h=5(cm ); (2)∵BD⊥AC,BD⊥PA, ∴BD⊥平面PAC. 又MN∥BD,∴MN⊥平面PAQ, ∴平面PAQ⊥平面PMN. 作OH⊥PQ于H,则OH之长即为所求. 作AG⊥PQ于G. 在Rt△PAQ中,AQ=, PQ= ∴AG= 再由得 OH= (cm). 【点评】 由于在棱锥中,随处可以找到解题必需的三角形,因此平面几何知识和解三角形的知识往往成为正确解题的关键. (2)截面法——空间图形的平面特写 解决球与多面体的组合问题,重要的是选好截面图,在截面中对寻找各量之间的关系,从而使空间问题转化为平面问题来解决. 【题2】一个圆锥形漏斗口的内周长为8πcm.漏斗深9.6cm,将一个球放进漏斗里,球的最高点比漏斗口所在平面高出2.4cm,求球的体积. 【解析】 作共同的轴截面图(如图),得等腰△PAB和圆O,球的最高点C,球心O和圆锥顶点P三点共线,D=AB∩PC,依题设: PD=9.6,CD=2.4,AD=. 过C作A1B1∥AB与PA、PB的延长线分别交于点A1、B1,则A1B1与圆O相切于C. 且有. ∴A1C=1.25AD=5. PA1= 记PA1与圆O的切点为E,则A1C=A1E, 且△PEO∽△PCA1, 得,PE=PA1-A1E=13-5=8, ∵OE=, 即得球半径R=,所以它的体积为(cm3). 【点评】 作出圆锥与球共同的轴截面,则圆锥与球的重要几何量与几何关系都在这一平面图形上充分展现出来了,通过对此平面图形的分析,即可求出球半径,从而求得球体积. (3)投影法——几何体的三视图 要作出空间物体在投影面上的投影,其实质就是通过物体上的点、线、面作出一系列的投影线与投影面的交点,并根据物体上的线、面关系,对交点进行恰当的连线. 8 6 【题3】已知某几何体的俯视图是如图5所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形. (1)求该几何体的体积; (2)求该几何体的侧面积. 【解析】 由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为边长为8,高为h1的等腰三角形,左、右侧面均为底边长为6,高为h2的等腰三角形. (1)几何体的体积为: (2) 正侧面及相对侧面底面边上的高为: , 左、右侧面的底边上的高为: 故几何体的侧面积为: (4)换底法——求三棱锥体积的妙法 三棱锥是最简单的棱锥,它的每个顶点都可以作为顶点,每个面都可以作为棱锥的底面,但无论如何换底面和锥顶,棱锥的体积不变. 【题4】 如图,是直角梯形,∠=90°,∥,=1,=2,又=1,∠=120°,⊥,直线与直线所成的角为60°. (Ⅰ)求证:平面⊥平面; (Ⅱ)求二面角的大小; (Ⅲ)求三棱锥的体积. 【解析】 解法一: (Ⅰ)∵ ∴, 又∵ ∴ (Ⅱ)取的中点,则,连结, ∵,∴,从而 作,交的延长线于,连结,则由三垂线定理知,, 从而为二面角的平面角 直线与直线所成的角为 ∴ 在中,由余弦定理得 在中, 在中, 在中, 故二面角的平面角大小为 (Ⅲ)由(Ⅱ)知,为正方形 ∴ (11)正四面体与正方体 在实践中,正方体是最常见的多面体;在理论上,所有的多面体都可看作是由正方体演变而来. 我们认定了正方体是多面体的“根基”. 我们在思考: (1)正方体如何演变出正四面体? (2)正方体如何演变出正八面体? (3)正方体如何演变出正三棱锥? (4)正方体如何演变出斜三棱锥? 【考题1】 (正四面体化作正方体解) 四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( ) A.3π B.4π C.3π D.6π 【说明】 本题如果就正四面体解正四面体,则问题就不是一个小题目了,而是有相当计算量的大题. 此时的解法也就沦为拙解. 【拙解】 正四面体棱长为底面ABC是边长为的正三角形△ABC的高线BD =·=(斜高VD=)△ABC的边心距HD=·= 正四面体V—ABC的高 正四面体外接球的半径为高的,即R=· 故其外接球的表面积为3π. 答案是A. 【联想】 、、的关系 正四面体的棱长为,这个正四面体岂不是由棱长为1的 正方体的6条“面对角线”围成? 为此,在棱长为1的正方体B—D1中, (1)过同一顶点B作3条面对角线BA1、BC1、BD; (2)将顶点A1,C1,D依次首尾连结. 则三棱锥B—A1C1D是棱长为的正四面体.于是正四面体问题可化归为对应的正方体解决. 【妙解】 从正方体中变出正四面体 以长为面对角线,可得边长为1的正方体ABCD—A1B1C1D1 ,这个正方体的体对角线长为,则其外接球的半径为,则其外接球的表面积为S=4πR2=4π ()2=3π 以为棱长的正四方体B—A1C1D以1为棱长的正方体有共同的外接球,故其外接球的表面积也为S=3π. 【寻根】 正方体割出三棱锥 在正方体中割出一个内接正四面体后,还“余下”4个正三棱锥. 每个正三棱锥的体积均为1/6,故内接正四面体的体积为1/3 . 这5个四面体都与正方体“内接”而“共球”. 事实上,正方体的内接四面体(即三棱锥)共有 =58个. 至此可以想通,正方体为何成为多面体的题根.查看更多