- 2021-04-15 发布 |
- 37.5 KB |
- 6页

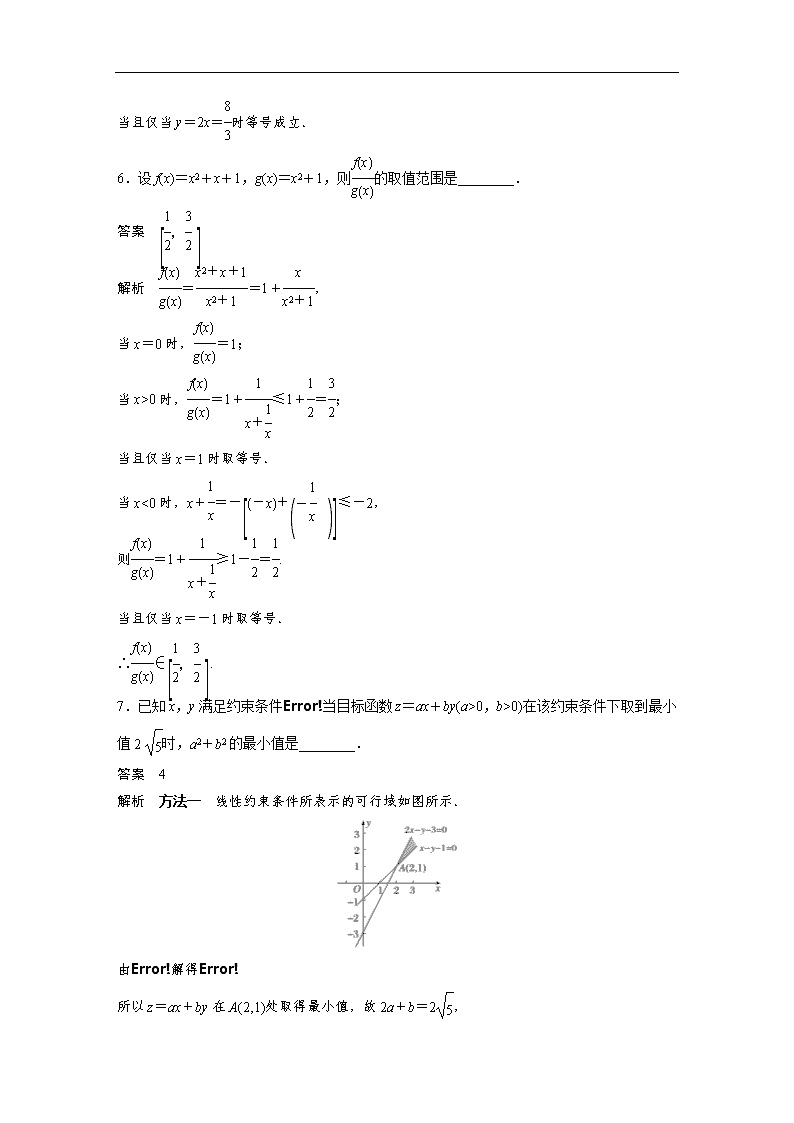
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年高考数学练习题汇总高考填空题分项练4 不等式
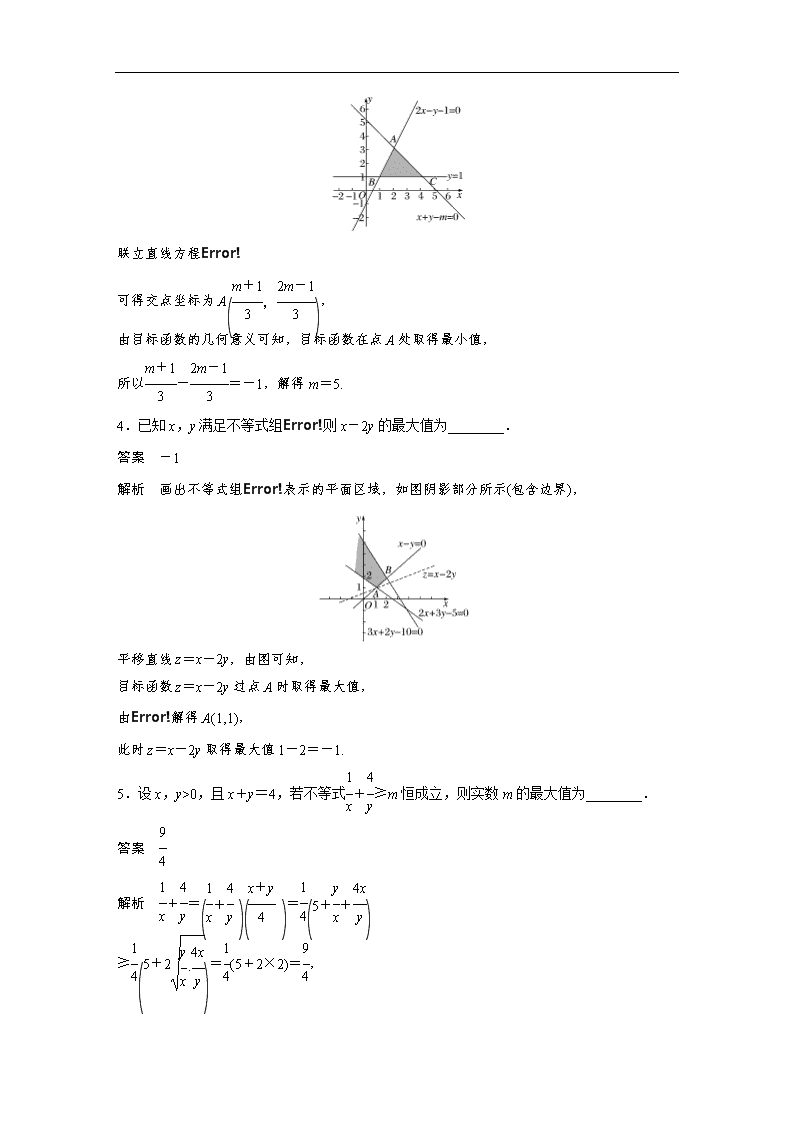
高考填空题分项练4 不等式 1.(2018·江苏海安测试)关于x的不等式x++b≤0(a,b∈R)的解集{x|3≤x≤4},则a+b的值为________. 答案 5 解析 由题意可得 解得⇒a+b=5. 2.若变量x,y满足约束条件且有无穷多个点(x,y)使得目标函数z=λx+2y取得最大值,则实数λ的值为________. 答案 -1 解析 约束条件表示的可行域为如图所示的阴影部分(包括边界). 目标函数z=λx+2y可化为y=-x+, 因为有无穷多个点(x,y)使得目标函数z=λx+2y取得最大值, 分析可得,直线y=-x+与直线BC:y=+1重合时目标函数取得最大值, 且有无穷多个点(x,y)满足要求, 所以-=,解得λ=-1. 3.已知实数x,y满足如果目标函数z=x-y的最小值为-1,则实数m=________. 答案 5 解析 绘制不等式组表示的平面区域如图阴影部分所示(含边界), 联立直线方程 可得交点坐标为A, 由目标函数的几何意义可知,目标函数在点A处取得最小值, 所以-=-1,解得m=5. 4.已知x,y满足不等式组则x-2y的最大值为________. 答案 -1 解析 画出不等式组表示的平面区域,如图阴影部分所示(包含边界), 平移直线z=x-2y,由图可知, 目标函数z=x-2y过点A时取得最大值, 由解得A(1,1), 此时z=x-2y取得最大值1-2=-1. 5.设x,y>0,且x+y=4,若不等式+≥m恒成立,则实数m的最大值为________. 答案 解析 +== ≥=(5+2×2)=, 当且仅当y=2x=时等号成立. 6.设f(x)=x2+x+1,g(x)=x2+1,则的取值范围是________. 答案 解析 ==1+, 当x=0时,=1; 当x>0时,=1+≤1+=; 当且仅当x=1时取等号. 当x<0时,x+=-≤-2, 则=1+≥1-=. 当且仅当x=-1时取等号. ∴∈. 7.已知x,y满足约束条件当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,a2+b2的最小值是________. 答案 4 解析 方法一 线性约束条件所表示的可行域如图所示. 由解得 所以z=ax+by在A(2,1)处取得最小值,故2a+b=2, a2+b2=a2+(2-2a)2=(a-4)2+4≥4. 方法二 由满足约束条件的可行域知,当目标函数过直线x-y-1=0与2x-y-3=0的交点(2,1)时取得最小值,所以有2a+b=2. 又因为a2+b2是原点(0,0)到点(a,b)的距离的平方,故当是原点到直线2a+b-2=0的距离时最小,所以的最小值是=2,所以a2+b2的最小值是4. 8.一批货物随17列货车从A市以v km/h的速度匀速到达B市,已知两地铁路线长为400 km,为了安全,两列货车的间距不得小于2 km(货车的长度忽略不计),那么这批货物全部运到B市,最快需要________ h. 答案 8 解析 这批货物从A市全部运到B市的时间为 t==+≥2 =8(h), 当且仅当v=100时,取等号. 9.(2018·江苏南京金陵中学期末)若对满足x+y+6=4xy的任意正实数x,y,都有x2+2xy+y2-ax-ay+1≥0,则实数a的取值范围为________. 答案 解析 因为4xy≤(x+y)2, 又因为正实数x,y满足x+y+6=4xy, 解得x+y≥3, 由x2+2xy+y2-ax-ay+1≥0, 可求得a≤x+y+, 根据双勾函数性质可知,当x+y=3时,x+y+有最小值, 所以a的取值范围为. 10.在R上定义运算:AB=A(1-B),若不等式(x-a)(x+a)<1对任意的实数x∈R恒成立,则实数a的取值范围是________. 答案 解析 (x-a)(x+a)=(x-a)[1-(x+a)] =-x2+x+a2-a, ∴-x2+x+a2-a<1, 即x2-x-a2+a+1>0对x∈R恒成立. ∴Δ=1-4(-a2+a+1)=4a2-4a-3<0, ∴(2a-3)(2a+1)<0,即-查看更多