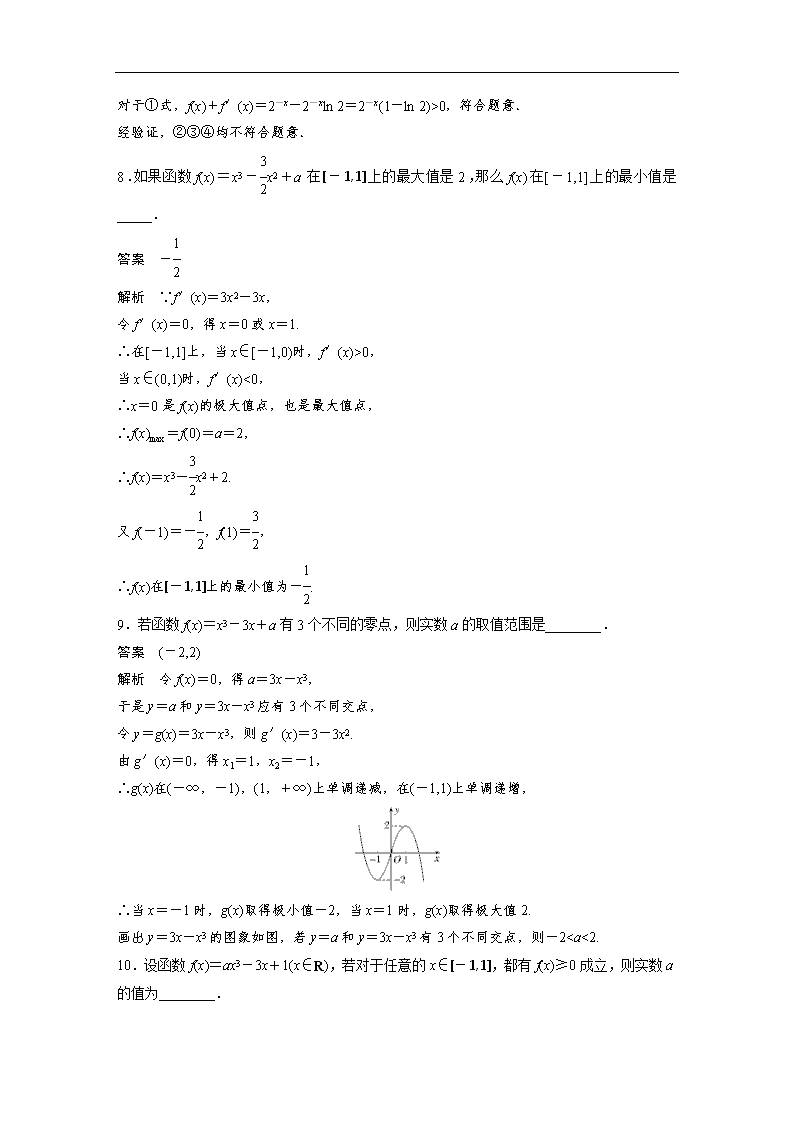2019年高考数学练习题汇总高考填空题分项练6 函数与导数
高考填空题分项练6 函数与导数
1.设曲线y=在点(3,2)处的切线与直线ax+y+1=0垂直,则a=________.
答案 -2
解析 ∵y==1+,∴y′=-.
∴曲线在点(3,2)处的切线斜率k=-.
∴-a=2,即a=-2.
2.设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为________.
答案 4
解析 依题意得f′(x)=g′(x)+2x,
所以f′(1)=g′(1)+2=2+2=4.
3.已知函数f(x)=在(-2,+∞)上单调递减,则a的取值范围是________.
答案
解析 ∵f′(x)=,且函数f(x)在(-2,+∞)上单调递减,∴f′(x)≤0在(-2,+∞)上恒成立,∴a≤.
当a=时,f′(x)=0恒成立,不合题意,应舍去.
∴a<.
4.已知a≤+ln x对任意x∈恒成立,则a的最大值为________.
答案 0
解析 令f(x)=+ln x,x∈,
则f′(x)=,
当x∈时,f′(x)<0,当x∈[1,2]时,f′(x)≥0,
∴f(x)在上单调递减,在[1,2]上单调递增,
∴f(x)min=f(1)=0,∴a的最大值为0.
5.若函数f(x)=x3+mx2-m2x+1(m为常数,且m>0)有极大值9,则m的值是________.
答案 2
解析 由f′(x)=3x2+2mx-m2=(x+m)(3x-m)=0,得x=-m或x=m,
当x变化时,f′(x)与f(x)的变化情况如下表:
x
(-∞,-m)
-m
m
f′(x)
+
0
-
0
+
f(x)
极大值
极小值
从而可知,当x=-m时,函数f(x)取得极大值9,
即f(-m)=-m3+m3+m3+1=9,解得m=2.
6.函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围是________.
答案 (0,1)
解析 f′(x)=3x2-3a=3(x2-a).
当a≤0时,f′(x)>0,
所以f(x)在(0,1)内单调递增,无最小值.
当a>0时,f′(x)=3(x-)(x+).
当x∈(-∞,-)和(,+∞)时,f(x)单调递增;
当x∈(-,)时,f(x)单调递减,
所以当0<<1,即0
0在f(x)的定义域上恒成立,即f(x)+f′(x)>0在f(x)的定义域上恒成立.
对于①式,f(x)+f′(x)=2-x-2-xln 2=2-x(1-ln 2)>0,符合题意.
经验证,②③④均不符合题意.
8.如果函数f(x)=x3-x2+a在[-1,1]上的最大值是2,那么f(x)在[-1,1]上的最小值是_____.
答案 -
解析 ∵f′(x)=3x2-3x,
令f′(x)=0,得x=0或x=1.
∴在[-1,1]上,当x∈[-1,0)时,f′(x)>0,
当x∈(0,1)时,f′(x)<0,
∴x=0是f(x)的极大值点,也是最大值点,
∴f(x)max=f(0)=a=2,
∴f(x)=x3-x2+2.
又f(-1)=-,f(1)=,
∴f(x)在[-1,1]上的最小值为-.
9.若函数f(x)=x3-3x+a有3个不同的零点,则实数a的取值范围是________.
答案 (-2,2)
解析 令f(x)=0,得a=3x-x3,
于是y=a和y=3x-x3应有3个不同交点,
令y=g(x)=3x-x3,则g′(x)=3-3x2.
由g′(x)=0,得x1=1,x2=-1,
∴g(x)在(-∞,-1),(1,+∞)上单调递减,在(-1,1)上单调递增,
∴当x=-1时,g(x)取得极小值-2,当x=1时,g(x)取得极大值2.
画出y=3x-x3的图象如图,若y=a和y=3x-x3有3个不同交点,则-20,即x∈(0,1]时,f(x)=ax3-3x+1≥0可化为
a≥-.
设g(x)=-,x∈(0,1],则g′(x)=.
所以g(x)在区间上单调递增,在区间上单调递减.
因此g(x)max=g=4,从而a≥4;
当x<0,即x∈[-1,0)时,f(x)=ax3-3x+1≥0可化为a≤-,g(x)在区间[-1,0)上单调递增,
因此g(x)min=g(-1)=4,从而a≤4.所以a=4.
11.海轮每小时使用的燃料费与它的航行速度的立方成正比,已知某海轮的最大航速为30千米/时,当速度为10千米/时,它的燃料费是每小时25元,其余费用(无论速度如何)是每小时400元.如果甲、乙两地相距800千米,则要使该海轮从甲地航行到乙地的总费用最低,它的航速应为________千米/时.
答案 20
解析 设航速为v千米/时(0≤v≤30),每小时的燃料费为m元,则m=kv3,
∵当v=10时,m=25,代入上式,得k=,
则总费用y=·m+×400=20v2+,
∴y′=40v-.令y′=0,得v=20.
经判断知当v=20时,y最小.
12.已知f(x)=x3-6x2+9x-abc,a0;②f(0)f(1)<0;③f(0)f(3)>0;④f(0)f(3)<0.
其中正确结论的序号是________.
答案 ②③
解析 方法一 由f(x)=x3-6x2+9x-abc,
得f′(x)=3x2-12x+9.
令f′(x)=0,得x=1或x=3.
当x<1时,f′(x)>0;
当13时,f′(x)>0.
∴当x=1时,f(x)有极大值,
当x=3时,f(x)有极小值.
∵函数f(x)有三个零点,
∴f(1)>0,f(3)<0,
且a<10,得a>0,因此f(0)0.
故正确结论的序号是②③.
方法二 由题设知f(x)=0有3个不同零点.如图所示.
设g(x)=x3-6x2+9x,
∴f(x)=g(x)-abc,f(x)有3个零点,需将g(x)的图象向下平移至如图所示位置.
观察图象可知,f(0)f(1)<0且f(0)f(3)>0.
故②③正确.
13.已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)0,即所求不等式的解集为(0,+∞).
14.(2018·苏州模拟)如果函数y=f(x)在其定义域内总存在三个不同实数x1,x2,x3,满足|xi-2|f(xi)=1(i=1,2,3),则称函数f(x)具有性质Ω.已知函数f(x)=aex具有性质 Ω,则实数a的取值范围为________.
答案
解析 由题意知,若f(x)具有性质Ω,则在定义域内|x-2|f(x)=1有3个不同的实数根,
∵ f(x)=aex,∴ =|x-2|·ex,
即方程=|x-2|·ex在R上有3个不同的实数根.
设g(x)=|x-2|·ex=
当x≥2时,g′(x)=(x-1)·ex>0,即g(x)在[2,+∞)上单调递增;
当x<2时,g′(x)=(1-x)·ex,g(x)>0,
∴g(x)在(-∞,1)上单调递增,在(1,2)上单调递减.
又∵ g(1)=e,g(2)=0,
∴方程=|x-2|·ex在R上有3个不同的实数根即函数g(x)与y=的图象有3个交点.
∴0<.